Оценка моделей проницаемости углепородного массива с учётом напряженно-деформированного состояния

Н.В. Ледяев¹, А.А. Черухин¹, К.С. Коликов², А.И. Маневич^{2, 3
1}  АО «СУЭК-Кузбасс», г. Ленинск-Кузнецкий, Российская Федерация
²  Национальный исследовательский технологический университет «МИСИС», г. Москва, Российская Федерация
³  Геофизический центр Российской академии наук, г. Москва, Российская Федерация
Горная Промышленность №6/ 2025 стр. 194-198

Резюме: Оценка проницаемости угольных пластов лежит в основе расчёта метанообильности выработок и определения параметров предварительной дегазации угольных пластов. Для адекватной оценки нагрузки на очистной забой по газовому фактору, проектирования схем дегазации и управления рисками аварийных ситуаций на угольных шахтах необходима корректная модель проницаемости углепородного массива. В работе рассмотрены основные эмпирико-аналитические зависимости, описывающие проницаемость угольных пластов как функцию напряжённо-деформированного состояния. Показано, что каждая из рассматриваемых моделей отражает собственный набор факторов: сорбционно-упругие деформации, термоупругий эффект, изменение пористости или прочности угольного пласта. Выполненный вариационный расчёт в диапазоне эффективных напряжений 0–50 МПа и глубин до 1500 м подтвердил общую закономерность: проницаемость падает нелинейно, причём главная зона снижения приходится на эффективное напряжение (σэфф) ≈ 5–15 МПа. Для надёжного трехмерного прогноза проницаемости углепородного массива необходим расширенный банк исходных данных. К ключевым параметрам относятся: литостатическое и тектоническое напряжения по карте глубин, модуль Юнга и коэффициент Пуассона вмещающих пластов, пористость и трещиноватость угля, коэффициенты адсорбции/десорбции, температурный градиент. Интеграция результатов в блочную ГГИС-модель позволяет учесть пространственную вариабельность свойств и перейти от усредненных оценок к локальной проницаемости, что принципиально необходимо для проектирования схем дегазационных скважин и расчёта их дебитов.

Ключевые слова: проницаемость угля, напряжённо-деформированное состояние, эффективное напряжение, сорбционно-упругие деформации, дегазация, угольные пласты

Для цитирования: Ледяев Н.В., Черухин А.А., Коликов К.С., Маневич А.И. Оценка моделей проницаемости углепородного массива с учётом напряженно-деформированного состояния. Горная промышленность. 2025;(6):194–198. https://doi.org/10.30686/1609-9192-2025-6-194-198

Информация о статье

Поступила в редакцию: 03.09.2025

Поступила после рецензирования: 23.10.2025

Принята к публикации: 24.10.2025

Информация об авторах

Ледяев Николай Владимирович – начальник управления противоаварийной устойчивости предприятий, АО «СУЭК-Кузбасс», г. Ленинск-Кузнецкий, Российская Федерация

Черухин Алексей Анатольевич – заместитель главного инженера по вентиляции шахты им. С.М. Кирова, АО «СУЭК-Кузбасс», г. Ленинск-Кузнецкий, Российская Федерация

Коликов Константин Сергеевич – доктор технических наук, профессор, заведующий кафедрой безопасности и экологии горного производства Горного института, Национальный исследовательский технологический университет «МИСИС», г. Москва, Российская Федерация; https://orcid.org/0000-0001-8831-1927; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Маневич Александр Ильич – научный сотрудник лаборатории геодинамики, Геофизического центра Российской академии наук, г. Москва, Российская Федерация; старший преподаватель кафедры безопасности и экологии горного производства Горного института, Национальный исследовательский технологический университет «МИСИС», г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

Оценка проницаемости угольных пластов лежит в основе корректного расчёта метанобильности выработок и определения параметров предварительной дегазации угольных пластов. Корректная модель проницаемости углепородного массива необходима для адекватной оценки нагрузки на очистной забой по газовому фактору, проектирования схем дегазации и управления рисками аварийных ситуаций на угольных шахтах ^[1].

Уголь как горная порода образуется вследствие многоступенчатого преобразования растительных остатков, происходящего под влиянием биохимических, геологических и тектонических факторов ^[2–4]. Пористость и трещиноватость, а значит и проницаемость, определяются как первоначальными условиями осадконакопления, так и последующими тектоническими процессами формирования угля. Нарастающие напряжения могут закрывать трещины и уменьшать фильтрационную способность массива, тогда как разгрузка, напротив, раскрывает кливак и повышает проницаемость ^[5]. Сорбционно-упругие процессы тоже играют роль: набухание матрицы при адсорбции газа сужает трещины, а усадка при десорбции способствует их раскрытию ^{[6; 7]}.

Тектоническая обстановка осадочного бассейна (стабильно-платформенная или активно-складчатая) определяет конфигурацию пластов и интенсивность разрывных нарушений ^[4]. Складки, разломы и зоны меланжа усложняют внутреннюю структуру угольных тел, создавая сети трещин различного масштаба и ориентации ^{[8; 9]}. В местах сильной тектонической нарушенности проницаемость, как правило, выше за счёт развёрнутой трещинной системы, что облегчает высвобождение метана. При этом разломы перераспределяют напряжения, формируя локальные зоны как повышенной, так и пониженной фильтрационной способности ^{[5; 9]}. На напряжённое состояние дополнительно влияют вмещающие породы: твёрдые песчаники или известняки концентрируют нагрузки, а пластичные глины, наоборот, способствуют их перераспределению ^{[7; 10; 11]}.

Материалы и методы

Пустоты в породе формируют каналы в форме пор, микротрещин, трещин. Структура массива схематически показана на рис. 1. Фильтрация сквозь массив возможна только в случае связанной системы потоковых каналов разного типа в направлении от А к Б. Если в результате изменения физико-механических условий исчезает связь по микротрещинам (рис. 1, б и в), то проницаемость обеспечивается поровой компонентой. При отсутствии переходчика (просачивания) по всем видам каналов массив будет непроницаем. Проницаемость породы (ее структура) могут изменяться под воздействием множества факторов.

Рис. 1 Схема структуры массива/ образца по [12]: 1 – направление фильтрации; 2 – трещины; 3 – микротрещины; 4 – поры; 5 – нетрещиноватый кристалл
Fig. 1 A schematic representation of the rock mass / sample structure according to [12]: 1 – filtration direction; 2 – fractures; 3 – microfractures; 4 – pores; 5 – non-fractured crystal

Функция проницаемости угольного пласта в общем виде может быть представлена как зависимость, которая учитывает структурные, тектонические, термодинамические и флюидодинамические характеристики угля:

k = f(σ, ε, φ, μ, T, P, d, ρ, θ),

где k – проницаемость, м²; σ – напряжения, Па, включая горизонтальные и вертикальные компоненты; ε – деформации, связанные с упругими, пластическими и хрупкими изменениями массива; φ – пористость угольного пласта, доля, %; μ – вязкость флюида, Па×c; T – температура, K; P – пластовое давление флюида, Па; d – размеры трещин и пор, м; ρ – плотность угля, кг/м³; θ – угол ориентации трещин, град.

Как было показано выше, факторов, воздействующих на проницаемость угля, большое количество. По этой причине учет их влияния по отдельности на проницаемость угля требует составления ансамбля моделей. Для моделирования исходной проницаемости угля требуется учет большого количества неопределенностей и верификация исходных данных, что невозможно в масштабных моделях. Эмпирико-аналитические модели, включающие в себя компоненты тензора сорбционных деформаций, связь тензора напряжений с тензором проницаемости, могут быть адекватно применимы для локальных участков и решения точечных задач (к примеру, для оценки проницаемости призабойного массива). Поэтому обычно в эмпирических моделях напряженно-деформированное состояние угольного пласта рассматривается в виде двух основных составляющих – среднего напряжения в массиве и глубины залегания пласта. Факторы сорбционных деформаций, порового давления применяются в моделях макро-масштаба.

Рассмотрим основные эмпирические модели, которые для удобства сравнения были приведены к единому аналитическому виду (табл. 1).

Таблица 1 Сравнение эмпирических зависимостей проницаемости угля от действующих напряжений
Table 1 A comparison of the empirical dependencies of coal permeability and effective stresses

Примечания: C – коэффициент чувствительности проницаемости к эффективному напряжению; a–эффективное напряжение; Δa_эфф – изменение эффективного напряжения; Δε_s – изменение сорбционной деформации; S – коэффициент чувствительности проницаемости к сорбционным деформациям; γ – коэффициент компенсации сорбционных деформаций; φ – пористость угольного пласта при действующем эффективном напряжении; φ₀ – исходная пористость угольного пласта при отсутствии действующих напряжений; α – текущее среднее нормальное напряжение; φ₁ – исходное среднее нормальное напряжение; E – текущий модуль Юнга горных пород при действующем среднем напряжении; E₀ – исходный модуль Юнга горных пород при отсутствии действующих напряжений.

Note: C – permeability sensitivity factor vs the effective stress; a–эффективное напряжение; Δa_эфф – changes in the effective stress; Δε_s – changes in the sorption deformation; S – permeability sensitivity factor vs the sorption deformation; γ – sorption deformation compensation factor; φ – coal seam porosity under effective stress; φ₁ – initial porosity of the coal seam in the absence of effective stresses; α – current average normal stress; φ₁ – initial average normal stress; E – current Young modulus of the rock at the current average stress; E₀ – initial Young modulus of the rock in the absence of effective stresses.

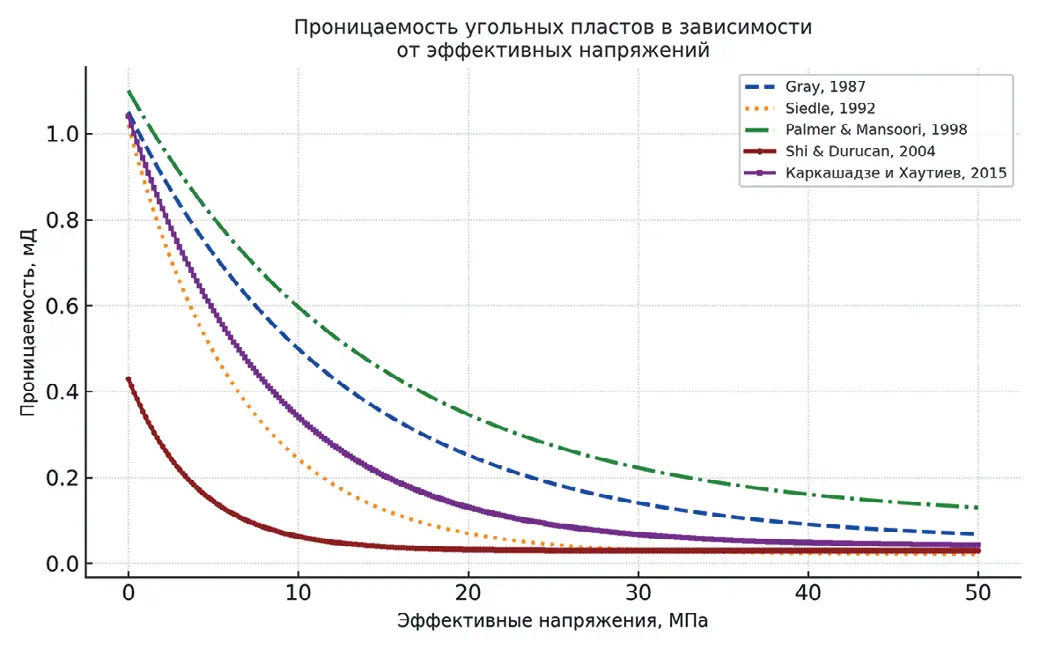
Рис. 2 Сводный график зависимостей проницаемости от эффективных напряжений в разных моделях (при принятых константах: C_p = 0.1 Па; i = 1×10⁸ м² (1 мД); Δε_s = 0.5; s = 0.5; γ = 0.5; φ₀ = 0.03; φ₁ = 0.02; E₀ = 5×10⁹; E = 3×10⁹)
Fig. 2 A cross plot of permeability dependencies on the effective stresses in different models (with the accepted constants: C_p = 0.1 Па; i = 1×10⁸ м² (1 мД); Δε_s = 0.5; s = 0.5; γ = 0.5; φ₀ = 0.03; φ₁ = 0.02; E₀ = 5×10⁹; E = 3×10⁹)

Результаты

Таким образом, основные эмпирические модели представлены в сравнительной табл. 1. Если использовать модель литостатического давления с учетом давления бокового отпора по модели А.Н. Динника [20], можно оценить изменение среднего и эффективного напряжения с глубиной. Эти данные можно использовать для моделирования исходной (начальной) проницаемости угольных пластов в ненарушенном массиве для последующего более точного моделирования или быстрой оценки проницаемости углепородного массива. На графике зависимости проницаемости от эффективного напряжения (рис. 2) показаны результаты расчётов по пяти моделям: [13; 15; 16; 17; 19].

Эти же расчеты можно привести в соответствие зависимости проницаемости от глубины залегания угольного пласта (рис. 3). Общая тенденция всех моделей заключается в нелинейном уменьшении проницаемости с ростом эффективного напряжения, что отражает физические процессы сжатия порового пространства и закрытия трещин в угольном пласте под действием внешних нагрузок. Однако каждая модель учитывает разные физические и геомеханические факторы, что приводит к различной чувствительности и форме кривых.

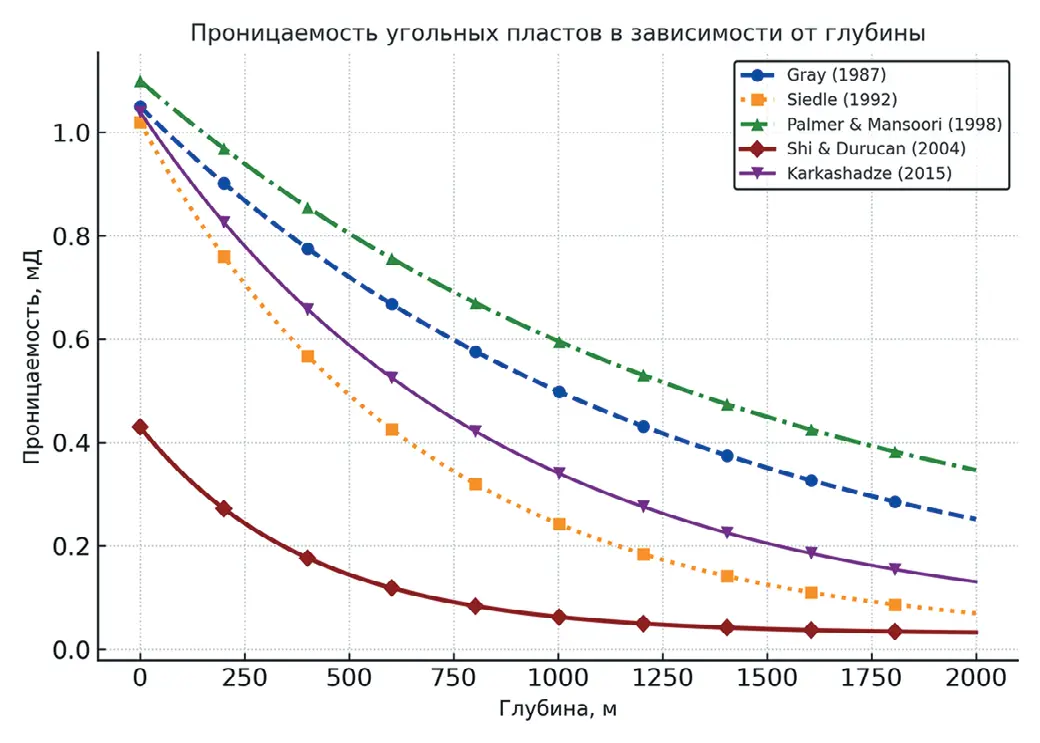
Рис. 3 Сводный график зависимостей проницаемости от эффективных напряжений в разных моделях (при принятых константах Cp = 0.1 Па-1; k0 = 1×10-12 м2 (1 мД); ∆εs = 0.5; S = 0.5; γ = 0.5; φ0 = 0.03; φ = 0.02; E0 = 5×109; E = 3×109)

Fig. 3 A cross plot of permeability dependencies on the effective stresses in different models (with the accepted constants Cp = 0.1 Па-1; k0 = 1×10-12 м2 (1 мД); ∆εs = 0.5; S = 0.5; γ = 0.5; φ0 = 0.03; φ = 0.02; E0 = 5×109; E = 3×109)

Массив исходных данных для моделирования проницаемости угольных пластов должен быть сформирован на основе геомеханических, физико-химических и термодинамических характеристик угольного массива, а также внешних воздействующих факторов, определяющих напряженно-деформированное состояние и сорбционно-деформационные процессы. Основой для моделирования служат геолого-технические параметры, такие как глубина залегания пласта, м, плотность горных пород, ρ, кг/м³, пористость угля, доли/проценты, начальная проницаемость, мД, и литологический состав углепородного массив.

Выводы

Эмпирические зависимости пригодны для крупномасштабных оценок. При дефиците детализированных данных опробования именно по моделям ^{[13; 15; 16; 17; 19]} можно быстро получить первый прогноз исходной проницаемости угольного пласта, опираясь на глубину залегания, литологию и средние значения напряжений. При этом ни одна модель не является универсальной. Учет сорбционных деформаций целесообразно определять по модели Stedle et al. ^{[14; 15]}; для глубоких пластов с высоким геотермическим градиентом целесообразно применение модели Palmer and Mansoori ^[16]; при выраженной анизотропии порового пространства наименее искаженные результаты даёт модель Shi and Durucan ^{[17; 18]}; учет упругих свойств дает модель Каркашадзе и Хаутиева ^[19]. Общая тенденция одинаково для всех моделей: по мере роста эффективного напряжения проницаемость падает нелинейно; основной градиент снижения наблюдается в диапазоне a_эфф = 5–15 МПа, после чего кривые выполняются.

Для надёжного трехмерного прогноза проницаемости углепородного массива необходим расширенный банк исходных данных. К ключевым параметрам относятся: литостатическое и тектоническое напряжение по карте глубин, модуль Юнга и коэффициент Пуассона вмещающих пластов, пористость и трещиноватость угля, коэффициенты адсорбции/десорбции, температурный градиент. Интеграция результатов в блочную ГПИС-модель позволяет учесть пространственную вариабельность свойств и перейти от усредненных оценок к локальной проницаемости, что принципиально необходимо для проектирования схем детазационных скважин и расчёта их дебитов.

Сноски

¹ АО «СУЭК-Кузбасс», г. Ленинск-Кузнецкий, Российская Федерация

² Национальный исследовательский технологический университет «МИСИС», г. Москва, Российская Федерация

³ Геофизический центр Российской академии наук, г. Москва, Российская Федерация

Список литературы

1. Литвинов А.Р., Коликов К.С., Ишхнели О.Г. Аварийность и травматизм на предприятиях угольной промышленности в 2010-2015 годах. Вестник научного центра по безопасности работ в угольной промышленности. 2017;(2):6–17.

2. Lloyd M.K., Trembath-Reichert E., Dawson K.S., Feakins S.J., Mastalerz M., Orphan V.J. Methoxyl stable isotopic constraints on the origins and limits of coal-bed methane. Science. 2021;374(6569):894–897. https://doi.org/10.1126/science.abg0241

3. Акматов Д.Ж., Евлоев Х.Ю., Меллер А.Д., Манукян Т.А., Чадин В.Н. Методика численного моделирования полей напряжений в районе размещения угольных шахт. Горная промышленность. 2023;(1):39–44. https://doi.org/10.30686/1609-9192-2023-1-39-44

4. Manevich A.I., Kolikov K.S., Egorova E.A. Geoecological aspects of stress-strain state modeling results of Leninsky coal deposit (Kuzbass, Russia). Russian Journal of Earth Sciences. 2019;19(4):ES4002. https://doi.org/10.2205/2019ES000663

5. Егорова Е.А., Коликов К.С., Мегид Х.А. Оценка проницаемости угольного пласта с учетом неоднородности в геологической структуре кровли. Горный журнал. 2016;(6):56–59. https://doi.org/10.17580/gzh.2016.06.02

6. Pan Z., Connell L.D. Modelling permeability for coal reservoirs: A review of analytical models and testing data. International Journal of Coal Geology. 2012;92:1–44. https://doi.org/10.1016/j.coal.2011.12.009

7. Lu S., Shi J., Jiao L., Ma Y., Li W., Sa Z. et al. A review of coal permeability models including the internal swelling coefficient of matrix. International Journal of Coal Science & Technology. 2024;11:50. https://doi.org/10.1007/s40789-024-00701-0

8. Столбова Н.Ф., Исаева Е.Р. Петрология углей. Томск: Изд-во Томского политехнического университета; 2013. 77 с. Режим доступа: https://www.geokniga.org/bookfiles/geokniga-petrologiya-ugley.pdf (дата обращения: 02.07.2025).

9. Batugin A., Kobylkin A., Kolikov K., Ivannikov A., Musina V., Khotchenkov E. et al. Study of the migrating mine gas piston effect during reactivation of tectonic faults. Applied Sciences. 2023;13(21):12041. https://doi.org/10.3390/app132112041

10. Robertson E.P., Christiansen R.L. A permeability model for coal and other fractured, sorptive-elastic media. SPE Journal. 2008;13(3):314–324. https://doi.org/10.2118/104380-PA

11. Connell L.D., Lu M., Pan Z. An analytical coal permeability model for tri-axial strain and stress conditions. International Journal of Coal Geology. 2010;84(2):103–114. https://doi.org/10.1016/j.coal.2010.08.011

12. Шмонов В.М., Витовтова В.М., Жариков А.В. Флюидная проницаемость пород земной коры. М.: Научный мир; 2002. 216 c. Режим доступа: https://www.geokniga.org/books/34016 (дата обращения: 02.07.2025).

13. Gray I. Reservoir engineering in coal seams, part 1 – the physical process of gas storage and movement in coal seams. SPE Reservoir Engineering. 1987;2(1):28–34. https://doi.org/10.2118/12514-PA

14. Seidle J. Fundamentals of coalbed methane reservoir engineering. PennWell Books; 2011. 470 p.

15. Seidle J.P., Jeansonne M.W., Erickson D.J. Application of matchstick geometry to stress dependent permeability in coals [Paper presented at the SPE Rocky Mountain Regional Meeting, Casper, Wyoming]. May 1992. https://doi.org/10.2118/24361-MS

16. Palmer I., Mansoori J. How permeability depends on stress and pore pressure in coalbeds: A new model. SPE Reservoir Evaluation & Engineering. 1998;1(6):539–544. https://doi.org/10.2118/52607-PA

17. Shi J.Q., Durucan S. A model for changes in coalbed permeability during primary and enhanced methane recovery. SPE Reservoir Evaluation & Engineering. 2005;8(4):291–299. https://doi.org/10.2118/87230-PA

18. Shi J.Q., Durucan S. Drawdown induced changes in permeability of coalbeds: a new interpretation of the reservoir response to primary recovery. Transport in Porous Media. 2004;56(1):1–16. https://doi.org/10.1023/B:TIPM.0000018398.19928.5a

19. Каркашадзе Г.Г., Хаутиев А.М.Б. Моделирование процесса дегазации угольного пласта через скважины с учетом геомеханических напряжений. Горный информационно-аналитический бюллетень. 2015;(2):235–242.

20. Динник А.Н. О давлении горных пород и расчет крепи круглой шахты. Инженерный работник. 1925;(7):1–12.