Мониторинг текущих траекторий перемещения автономных тяжёлых платформ по карьерным маршрутам горнорудных предприятий

И.В. Чичерин, Б.А. Федосенков, Д.М. Дубинкин
Кузбасский государственный технический университет им. Т.Ф. Горбачева, г. Кемерово, Российская Федерация
Горная Промышленность №5 / 2021 стр. 76-83

Резюме: С целью получения информации о формируемых текущих траекториях беспилотных карьерных самосвалов в программно-аппаратных комплексах автоматизированной системы диспетчеризации, установленной на борту автономных тяжелых платформ, текущим траекториям платформ ставятся в соответствие одномерные (скалярные) непрерывные сигналы (далее преобразуемые в дискретные цифровые) с время-зависимой мгновенной частотой, так называемые чирп-сигналы. В качестве рабочего инструмента для проведения вычислительных процедур в программно-аппаратном модуле выбрано распределение Вигнера-Вилле. В основу данного распределения положены вейвлет-функции базиса Габора и алгоритм вейвлет-поиска соответствия. Выбор вейвлетов Габора объясняется их синусоидально-подобной формой, поскольку они представляют собой промодулированные окном Гаусса синусоидальные сигналы. Анализируемые 1D-сигналы, свидетельствующие о текущем положении автономных тяжелых платформ на маршруте, также являются синусоидально-подобными. Полученный в результате аппроксимации вейвлет-ряд далее преобразуется во время-частотное распределение Вигнера, по которому формируется соответствующая текущих траекторий. В качестве примера приведены реконструкции время-частотных распределений, соответствующие отклонению текущих траекторий влево и вправо от номинальной осевой траектории. На основании полученных результатов приводятся выводы о том, что наиболее целесообразными способами для осуществления мониторинга текущих траекторий движения автономных тяжелых платформ и процедурами обработки соответствующих сигналов являются операции, реализуемые в автоматизированных подсистемах внешнего и автономного управления и базирующиеся на таких понятиях, как вейвлет-распределения класса Коэна, избыточный словарь вейвлет-функций Габора, алгоритм вейвлет-поиска соответствия и отображение чирп-сигналов, а также стационарных по частоте сигналов о текущих траекториях автономных тяжелых платформ, представленных в вейвлет-среде. Представленные процедуры реализации текущего мониторинга перемещения автономных тяжелых платформ по карьерным маршрутам и процесса обработки сигналов о динамическом изменении текущих траекторий, заложенные в программно-аппаратные комплексы подсистем автономного и внешнего управления системы «Умный карьер», обеспечивают адекватное выполнение требуемых функций. Внедрение принципов автоматизированного управления беспилотными карьерными транспортными средствами позволяет оптимизировать трудозатраты на эксплуатацию горного оборудования, снижать расходы на текущие работы, привлекать высококвалифицированных специалистов для освоения и рабочей эксплуатации инновационной транспортной техники.

Ключевые слова: автономные тяжелые платформы, текущие траектории, вейвлеты Габора, алгоритм вейвлет-поиска соответствия, чирп-сигналы, распределения класса Коэна

Благодарности: Работа выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации в рамках соглашения № 075-11-2019-034 от 22.11.2019 г. с ПАО «КАМАЗ» по комплексному проекту «Разработка и создание высокотехнологичного производства автономных тяжелых платформ для безлюдной добычи полезных ископаемых в системе “Умный карьер”», при участии ФГБОУ ВО «Кузбасский государственный технический университет имени Т.Ф. Горбачева» в части выполнения научно-исследовательских, опытно-конструкторских и технологических работ. Авторы выражают благодарность сотрудникам института информационных технологий, машиностроения и автотранспорта ФГБОУ ВО «Кузбасский государственный технический университет имени Т.Ф. Горбачева» за содействие в размещении рукописи статьи в редакции журнала.

Для цитирования: Чичерин И.В., Федосенков Б.А., Дубинкин Д.М. Мониторинг текущих траекторий перемещения автономных тяжёлых платформ по карьерным маршрутам горнорудных предприятий. Горная промышленность. 2021;(5): 76–83. DOI: 10.30686/1609-9192-2021-5-76-83.

Информация о статье

Поступила в редакцию: 19.08.2021

Поступила после рецензирования: 15.09.2021

Принята к публикации: 16.09.2021

Информация об авторах

Чичерин Иван Владимирович – кандидат технических наук, доцент, заведующий кафедрой информационных и автоматизированных производственных систем, Кузбасский государственный технический университет имени Т.Ф. Горбачева, Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Федосенков Борис Андреевич – доктор технических наук, профессор, профессор кафедры информационных и автоматизированных производственных систем, Кузбасский государственный технический университет имени Т.Ф. Горбачева, Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Дубинкин Дмитрий Михайлович – кандидат технических наук, доцент, доцент кафедры металлорежущих станков и инструментов, Кузбасский государственный технический университет имени Т.Ф. Горбачева, Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

В ранее опубликованных исследованиях по автономным транспортным средствам (в том числе и по беспилотным карьерным самосвалам) были проанализированы вопросы: формирования маршрутных параметров и моделей перемещения карьерных автономных тяжелых платформ (АТП), сформулированные в рамках интегративной системы управления «Умным карьером» [1]; мониторинга окружающей среды с помощью наземных колесных транспортных модулей [2]; современного состояния техники и технологий в области автономного управления движением транспортных средств на горнорудных карьерах [3; 4]; повышения технических характеристик карьерных самосвалов [5]; наблюдения за окружающей обстановкой при движении беспилотных транспортных средств (БТС) [6]; интеллектуализации БТС [7]; теории, алгоритмизации и реализации технологических процедур в программно-аппаратном комплексе интеллектуальных БТС [8]; систематизации и выработки терминологии относительно систем автоматизации для движущихся по дорогам общего пользования транспортных средств [9]; методологии, проектирования, разработки логических основ искусственного интеллекта для систем управления движением БТС [10; 11] и исследования возможностей технического зрения для беспилотных автомобилей [12].

Вопросы, проанализированные в этих проектах, будучи приложенными к горнорудным предприятиям, инициируют приток высококвалифицированной рабочей силы, способной внедрять и обслуживать инновационную технику, требующую знаний и умений нового уровня: информационных технологий и автоматизации на базе цифровой электроники и компьютерно-интегрированных систем, широкой цифровизации административно-хозяйственных комплексов. Такого рода технологии широко применяются в том числе и при разработке проектов, связанных с созданием беспилотной, автономной горранспортной техники, предназначенной для работы в системах безлюдной технологии.

В представленном исследовании, в частности, рассмотрены принципы управления передвижением АТП по прямым и искривлённым технологическим маршрутам, заданным в так называемом формате сплайн-фреймов – S-фреймов [1].

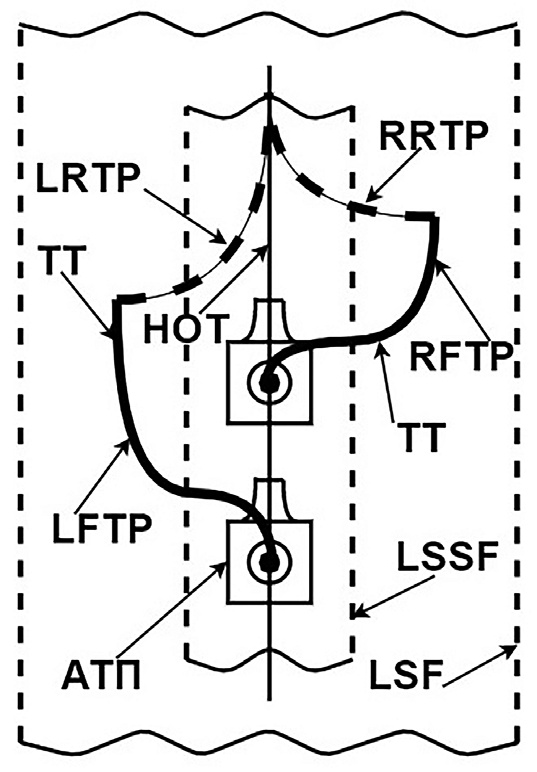
Рис. 1 Схема возникновения возмущенных прямых (девиационных) и формирования обратных восстанавливающих траекторий АТП на прямом участке S-фрейма некоторого маршрута при уходе ТТ влево и вправо от НОТ: АТП – автономная тяжелая платформа; LSF (Local Spline Frame) – локальный S-фрейм; LSSF (Local Sub-Spline Frame) – локальный суб-S-фрейм; НОТ – номинальная осевая траектория движения АТП; LFTP / RFTP (Left Forward Transient Process / Right Forward Transient Process) – соответственно прямые переходные процессы девиации текущей траектории движения АТП влево / вправо от НОТ; LRTP / RRTP (Left Reverse Transient Process / Right Reverse Transient Process) – соответственно обратные переходные процессы восстановления НОТ при девиации текущей траектории (ТТ) движения АТП влево / вправо от НОТ

Fig. 1 Diagram of occurrence of disturbed forward (deviation) and formation of reverse recovery paths of AHP on the direct section of S-frame of some route when TT leave to the left and right of the NAT: АТП – autonomous heavy platform (AHP); LSF – Local Spline Frame; LSSF – Local Sub-Spline Frame; НОТ – nominal axial trajectory (NAT) of AHP; LFTP / RFTP (Left Forward Transient Process / Right Forward Transient Process) – the forward transient processes of the current AHP trajectory deviation to the left / right from the NAT, respectively; LRTP / RRTP (Left Reverse Transient Process / Right Reverse Transient Process) – the reverse transient processes of the NAT recovery in case of the current AHP trajectory (ТТ / CT) deviation to the left / right from the NAT, respectively

На рис. 1 схематично изображены на прямом S-фрейме две девиационные текущие траектории с указанием прямых (отклоняющихся от номинальной осевой траектории – НОТ) и обратных (возвращающихся к НОТ) текущих траекторий (ТТ). В программно-аппаратном комплексе, входящем в состав автоматизированной системы диспетчеризации, прямым и обратным переходным процессам ставятся в соответствие одномерные (скалярные) информационные чирп-сигналы [13], [2] то есть сигналы x(t) с время-зависимой частотой.

Через x(t)_l и x(t)_r обозначим обобщенную координату движения АТП при девиации траектории соответственно влево и вправо от номинальной осевой траектории по ходу движения.

Концепция текущего мониторинга траекторий АТП

С целью информативно-полной и семантически-прозрачной обработки сигналов в программно-аппаратных комплексах подсистем автономного и внешнего управления [1], в программные комплексы последних введены фрагменты, обеспечивающие формирование так называемых вейвлет-функций [13; 14] и квадратичных вейвлет-распределений класса Коэна [15; 16].

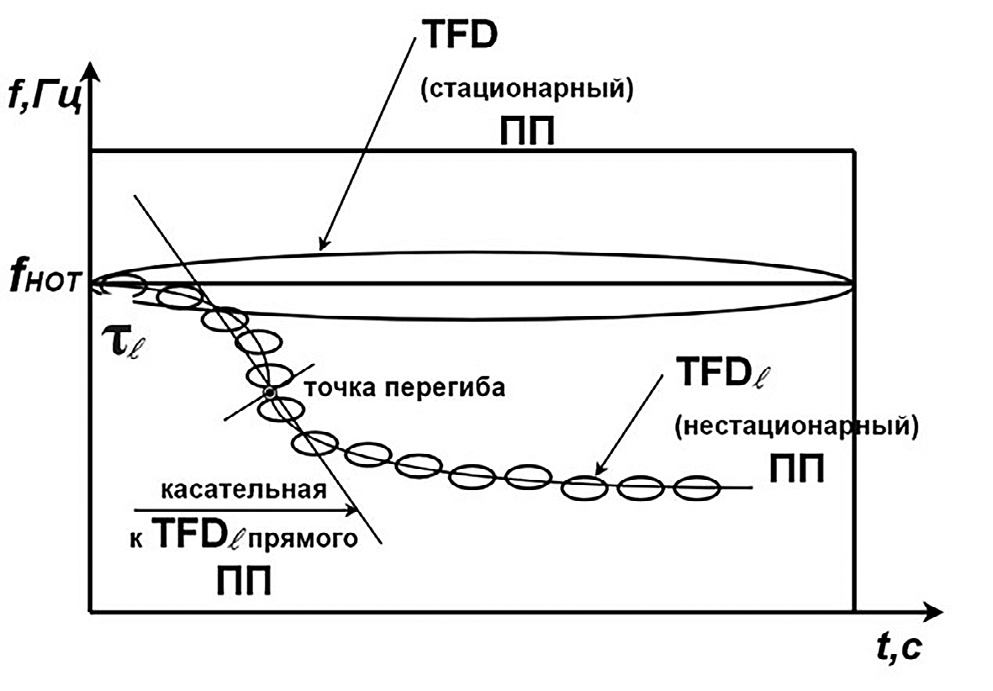
Рис. 2 Карта Вигнера, отображающая в вейвлет-среде стационарный сигнал и нестационарный с понижающейся частотой, соответствующий уходу ТТ АТП влево от НОТ

Fig. 2 Wigner map displaying stationary signal and nonstationary with a decreasing frequency, corresponding to the AHP CT moving to the left of the NAT

На рис. 2 представлен вид-реконструкция вейвлет-карты (W-карты, карты Вигнера) [17; 18], на которой в формате время-частотных распределений Вигнера изображен сигнал ухода ТТ АТП влево от НОТ, а на рис. 3 – сигнал отклонения ТТ АТП вправо. При этом девиации ТТ влево от НОТ соответствует задаваемое в программно-аппаратном комплексе АСД снижение частоты сигнала обобщенной переменной x(t)l, а девиации ТТ вправо от НОТ – повышение частоты сигнала x(t)r. На рис. 2 и 3 моменты τl и τr соответствуют началу девиации ТТ АТП влево / вправо от НОТ под действием автономно-спорадических возмущений, вызываемых возникновением на маршруте АТП каких-либо препятствий.

Распределение Вигнера, определяющее в нашем исследовании, является многомерно-квадратичным и имеет вид интегральной функции:

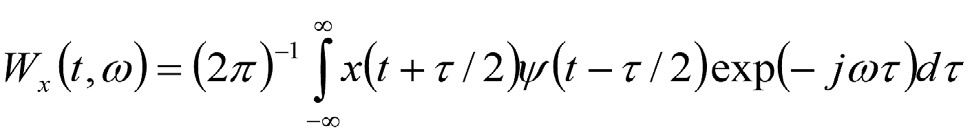
Отсюда видно, что распределение Вигнера представляет собой взаимно-корреляционную функцию сигнала с время-частотным атомом (вейвлет-функцией) из определенной совокупности (вейвлет-тезауруса, или словаря) при его временном и частотном смещении относительно этих атомов. Таким образом, функция распределения Вигнера является двумерной или даже трехмерной функцией, поскольку интенсивность сигнала (значение взаимно-корреляционной функции) в двумерной время-частотной плоскости может быть охарактеризована как третья координата. Следовательно, функция распределения Вигнера характеризует распределение плотности энергии (интенсивности) сигнала.

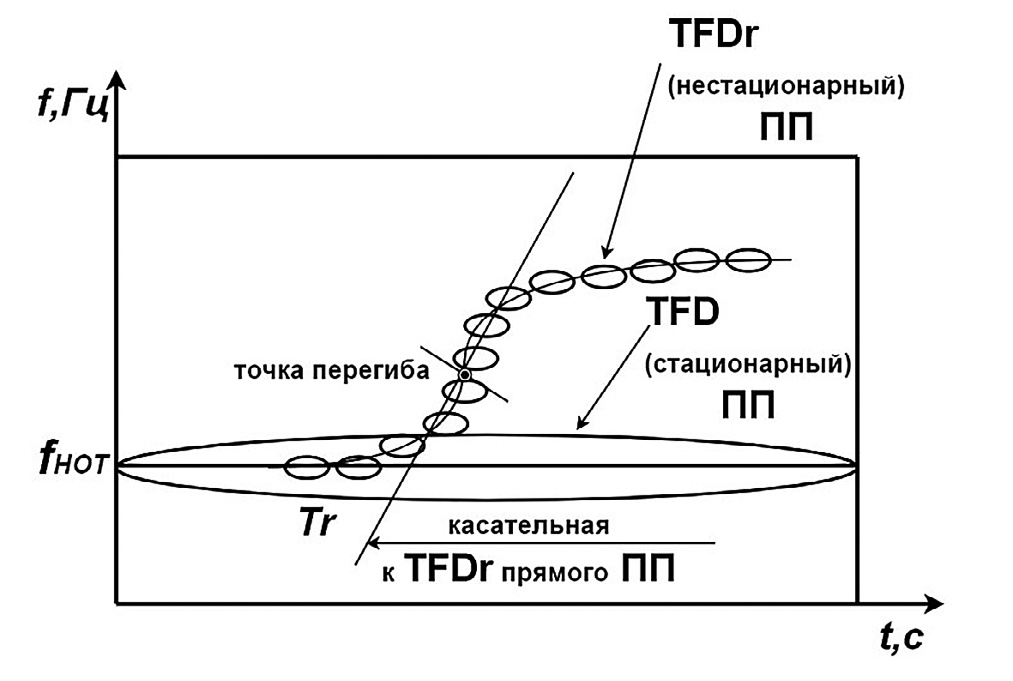
Рис. 3 Карта Вигнера, отображающая в вейвлет-среде стационарный сигнал и нестационарный с повышающейся частотой, соответствующий уходу ТТ АТП вправо от НОТ

Fig. 3 Wigner map displaying the stationary signal and nonstationary with an increasing frequency, corresponding to the AHP CT departure to the right of the NAT

Время-частотный атом-аппроксимант – вещественный вектор, имеющий вид:

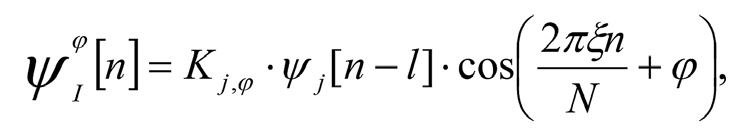
где K_j,φ задает единичную норму вектора Ψ_I ^φ[n], а начальная фаза φ оптимизируется так, чтобы максимизировать скалярное произведение атома с остатком сигнала.

На рис. 4 слева показан переходный процесс, соответствующий девиации ТТ АТП влево от НОТ в 1D-формате; кроме того, здесь же представлены реконструированные по алгоритму вейвлет-поиска соответствия (ВПС) [13; 18; 19] сигнал, а также ошибка аппроксимации сигнала. Справа представлено многомерное отображение того же сигнала в виде распределения Вигнера.

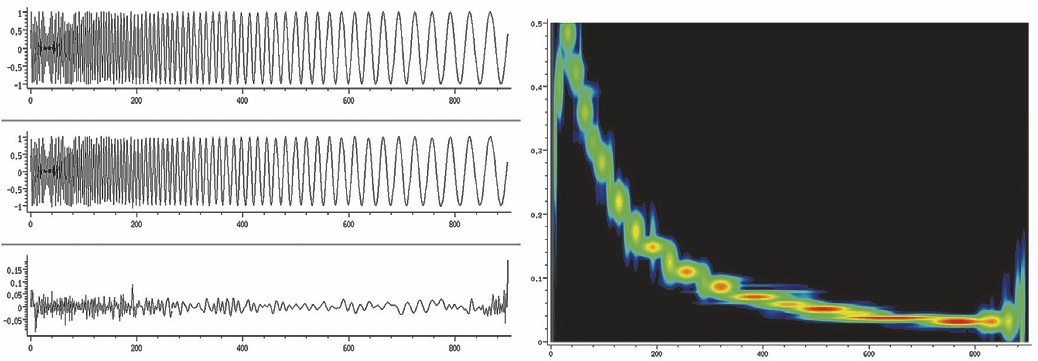
Рис. 4 Переходные процессы в одномерном формате и в виде отображения Вигнера, соответствующие отклонению ТТ АТП от НОТ влево

Fig. 4 Transient processes in onedimensional format and in the form of Wigner representation, corresponding to the AHP CT deviation from the NAT to the left

Характер 1D-сигнала ТТ, девиирующей вправо от НОТ (рис. 3), определяется апериодикой 2-го порядка и сформирован из отдельных время-частотных атомов (ВЧА) [20; 21] в соответствии с алгоритмом вейвлет-поиска соответствия. По параметрам отображения такого нестационарного процесса определяются параметры предстоящего режима, режима динамического модального управления, возвращающего ТТ к НОТ. Кроме того, здесь же приведена форма вейвлет-отображения стационарного по частоте fнот сигнала. Подобная процедура реализуется и для сигнала, соответствующего уходу ТТ влево от НОТ (см. рис. 2).

Процедуры обработки сигналов о текущих траекториях АТП

Визуально-графическое отображение технологического сигнала, характеризующего динамику ТТ АТП на маршруте, формируется в многомерной вейвлет-среде, что позволяет информационно ёмко и семантически прозрачно представлять перемещение АТП в карьере.

Для того чтобы отслеживать движение АТП по текущим траекториям, предложен способ соответствия специфического 1D-информационного сигнала с время-зависимой мгновенной частотой – чирп-сигнала – процессу формирования ТТ.

Так, процессу отклонения ТТ от НОТ влево ставится в соответствие экспоненциальный чирп-сигнал с уменьшающейся частотой, а процессу отклонения ТТ от НОТ вправо – экспоненциальный сигнал с возрастающей частотой. При этом начальный участок ТТ, обусловленный её девиацией от НОТ вследствие наличия (обнаружения радарно-лидарно-сонарной системой) какого-либо препятствия или встречной АТП на маршруте, описывается двухэкспоненциальной зависимостью вида (см. рис. 3):

x(t) = k_н [1 – (T₃ / (T₃ – T₄)) (exp(–t /T₃) + (T₄ / (T–t /T₃ – T₄)) (exp(–t /T₄)].

Этот участок ТТ именуется автономно-спорадическим, поскольку определяется случайными, возникающими время от времени, внешними возмущениями.

Конечный участок ТТ формируется принудительно (например, под действием динамического модального регулятора [22]; в этом случае его уместно именовать принудительно-модальным). Таким образом, принудительное техническое средство устраняет возникшую на начальном автономно-спорадическом участке ТТ девиацию её от НОТ, приводя ТТ к номинальной осевой траектории. Конечный участок ТТ может характеризоваться как двухэкспоненциальным сигналом, так и одноэкспоненциальным (см. рис. 2):

x(t) = k_к [1 – (exp(–t / T)],

где T₃, T₄, T, k_н, k_к – соответственно постоянные времени сигнала начального участка ТТ и конечного; kн и kк – коэффициенты передачи для сигнала, соответствующего начальному и конечному участкам ТТ.

При отображении чирп-сигналов в вейвлет-среде используются квадратичные вейвлет-распределения класса Коэна. В наших исследованиях в качестве рабочего инструмента применяется вейвлет-распределение Вигнера, в качестве вспомогательного (настроечного) – вейвлет-распределение Чуи-Уилльямса.

Для преобразования 1D-чирп-сигналов в вейвлет-распределения в работе используется адаптивная аппроксимация на базе алгоритма вейвлет-поиска соответствия. В качестве базисных вейвлет-функций используются вейвлеты в составе избыточного словаря [13; 18], в котором, помимо вейвлетов Габора, содержатся вейвлеты из базисов Хевисайда, Гаусса, Дирака и Фурье.

При этом габоровская вейвлет-фукция, представляющая собой модулированную функцией Гаусса (с конечным носителем) гармоническую структуру, имеет вид:

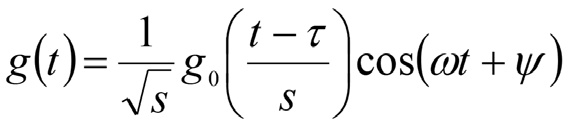
где g₀(t)– модулирующая материнская вейвлет-функция Гаусса; ω и τ – текущие частота и смещение; ψ – начальная фаза гармонического сигнала.

Использование вейвлет-функций Габора в качестве основных продиктовано их синусоидально-подобной формой. С учетом того что вейвлеты Габора представляют собой модулированные функцией Гаусса синусоидальные сигналы, достижение критерия оптимального выбора из словаря соответствующего вейвлета (что соответствует оптимизации процедуры аппроксимации чирп-сигналов) является достаточно очевидным и комфортным.

Оптимизация процедуры аппроксимации определяется максимизацией скалярного произведения:

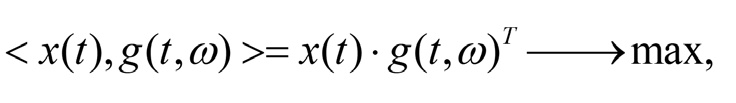
где x(t) – аппроксимируемый фрагмент чирп-сигнала;

g(t, ω) – выбираемая из словаря вейвлет-функция. При этом достижение указанного критерия обеспечивается варьированием четырёх параметров вейвлета Габора:

– τ – смещение вейвлета по оси времени t;

– s – масштаб вейвлета (величина поддержки вейвлета на оси t);

– ξ (здесь обозначено через ω) – частота вписанной в функцию Гаусса синусоиды;

– ψ – начальная фаза синусоиды.

Пятый параметр – мгновенная амплитуда вейвлета – исключается из списка варьируемых параметров, поскольку при проецировании анализируемого сигнала на вейвлет-словарь все отбираемые из него вейвлеты, так же, как и анализируемые чирп-сигналы, нормализуются по квадратичной единичной норме:

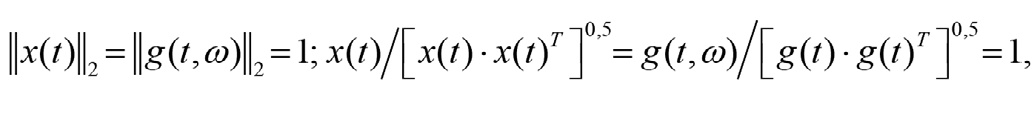
где квадратичная норма сигнала есть расширенное понятие модуля на бесконечномерное пространство.

При этом частота варьирования значений параметров вейвлетов Габора возрастает от τ к ψ. Отметим, что значения параметров τ, s, ξ содержатся в соответствующих разделах избыточного словаря Габора, а параметр ψ варьируется вне словаря в диапазоне [0, 2π].

В результате аппроксимации определенного чирп-сигнала получаем его аппроксиманту в виде вейвлет-ряда

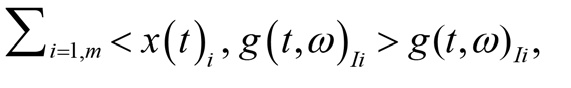
где x(t)_i – i-й анализируемый участок чирп-сигнала x(t); g (t, ω)Ii – вейвлет-функция Габора, выбранная на i-й итерации и обладающая индексом параметров Ii = [τ, s, ξ, ψ]. Для вейвлет-сигналов словаря Габора вида

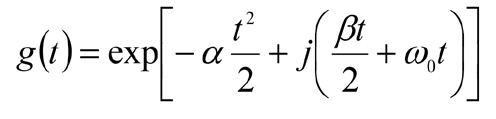
т.е. сигналов, представляющих собой гармоники, модулированные функцией Гаусса, распределение Вигнера определяется как

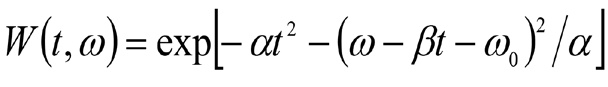
При использовании словаря с вейвлет-функциями Габора распределение Вигнера всегда положительно [13; 18]. Данное свойство позитивности распределения соответствует его семантической особенности – способности отображать энергетическую плотность исследуемого сигнала. Если коэффициент α – мал, то энергия сигнала концентрируется эллипсообразно вдоль линии с частотой ω = ω0 + βt, являющейся производной фазы d[(βt / 2 + ω₀)]/dt. При α=0 (при единичной модуляции) получаем частотно-времязависимый сигнал:

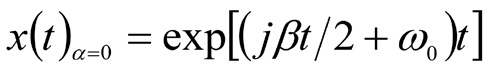
распределение Вигнера которого вырождается в дельтафункцию с наклоном β на время-частотной плоскости (рис. 5, а):

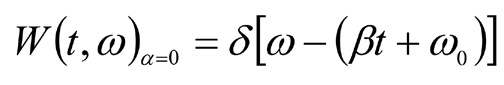
Отсюда видно, что вся энергия локализуется вдоль мгновенной частоты (βt + ω₀). При β=0 (и α=0 ) энергия концентрируется вдоль горизонтальной линии на частоте ω₀ = const (рис. 5, б):

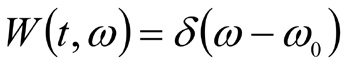
Фактическая расчетная дискретность и частотно-временной разброс отображения одномерного сигнала в виде его представления в 2D-пространстве (МСД-карты, то есть карты модифицированного сигнала динамики текущей траектории АТП) (рис. 6) объясняется спецификой алгоритма вейвлет-поиска соответствия, особенностями используемых вейвлет-функций и исходной дискретностью анализируемых сигналов [18].

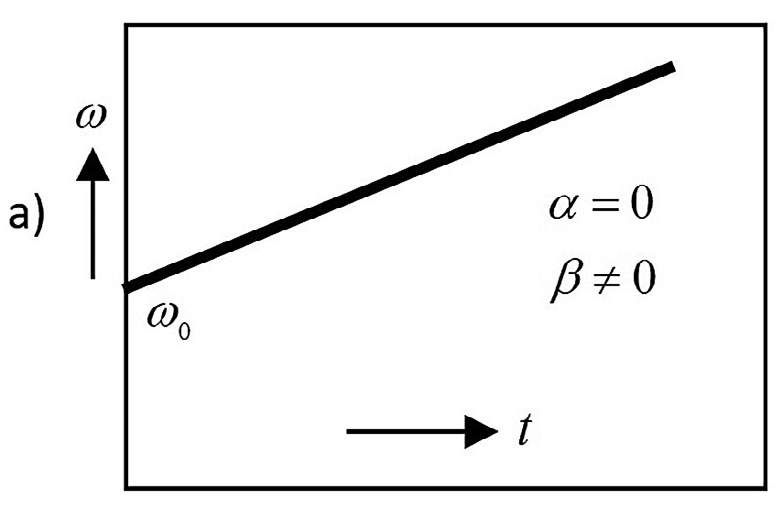
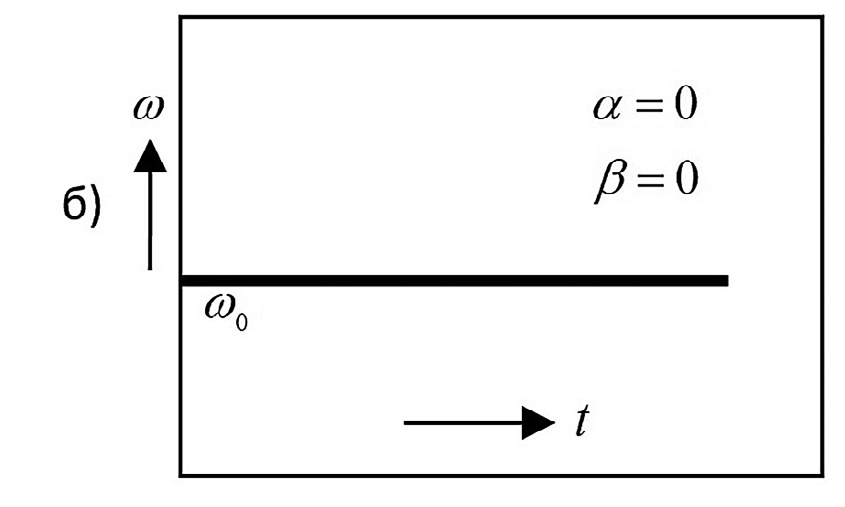
Рис. 5 Распределение Вигнера для: а – гармонического сигнала с время-зависимой частотой; б – гармонического сигнала с постоянной частотой

Fig. 5 Wigner distribution for: а – a harmonic signal with a time-dependent frequency; б – a harmonic signal with a constant frequency

Сигналу, представленному на рис. 6, а, соответствует движение АТП по девиационной текущей траектории с её отклонением вправо от НОТ, а сигналу на рис. 6, б – движение АТП по номинальной осевой траектории.

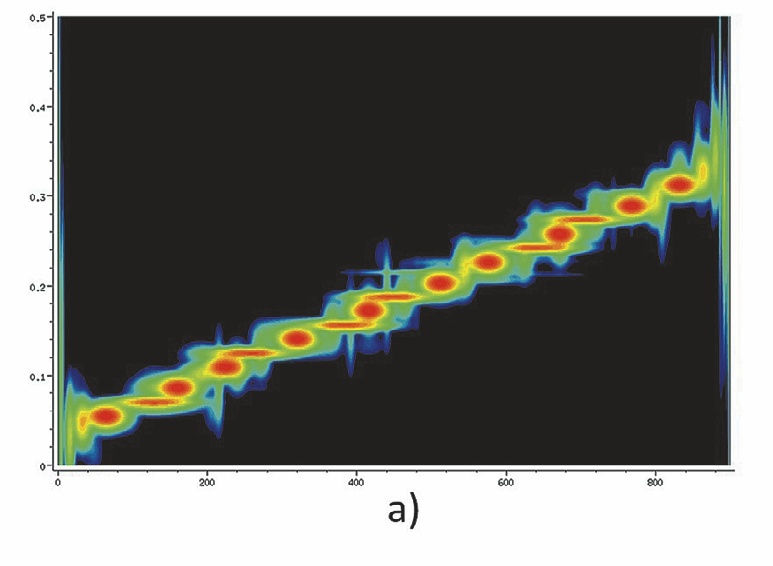
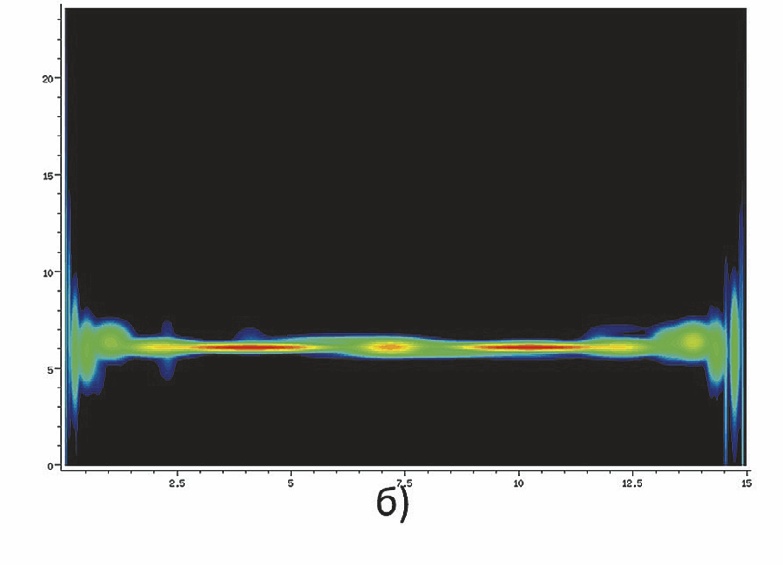
Рис. 6 Расчетные распределения Вигнера реальных сигналов для случаев: а – формула (1) и б – (2)

Fig. 6 Estimated Wigner distributions of real signals for the cases: а – formula (1) and б – (2)

Заметим, что с целью адекватного выполнения процедур по проецированию текущих чирп-сигналов на словарь вейвлет-функций на предварительном этапе обработки чирп-сигналов последние подвергаются следующим операциям:

1. центрирования (исключения из сигналов постоянной составляющей);

2. дискретизации (преобразования центрированных сигналов посредством АЦП);

3. нормализации («выравнивания» мгновенных амплитуд дискретизированных сигналов о ТТ движения АТП, а также отбираемых вейвлет-функций из словаря, то есть приведения их к единичной норме – см. выше).

Заключение

Описанные в исследовании способы мониторинга текущих траекторий движения АТП и процедуры обработки соответствующих сигналов основаны на следующих понятиях и результатах:

1. вейвлет-распределения класса Коэна;

2. избыточный словарь вейвлет-функций Габора;

3. алгоритм вейвлет-поиска соответствия;

4. отображения чирп-сигналов с линейно-возрастающей частотой и стационарного по частоте сигнала о текущих траекториях АТП, представленные в вейвлет-среде;

5. исполнение на предварительном этапе обработки сигналов процедур центрирования, дискретизации и нормализации анализируемых сигналов о текущих траекториях АТП, а также отбираемых из словаря вейвлетов на каждой итерации определенных вейвлет-функций.

Представленные процедуры реализации текущего мониторинга перемещения АТП по карьерным маршрутам и процесса обработки сигналов о динамическом изменении текущих траекторий, заложенные в программно-аппаратные комплексы подсистем автономного и внешнего управления системы «Умный карьер», обеспечивают адекватное выполнение требуемых функций.

Внедрение подобных структур автоматизации горнотранспортной техники в технологическое хозяйство горнорудных предприятий, расположенных в горных регионах, дает возможность привлекать квалифицированных специалистов для внедрения и эксплуатации нового высокотехнологичного оборудования, что, в свою очередь, способствует формированию условий для перспективного устойчивого социально-экономического развития горных территорий.

Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Conflict of interests
The authors state that there is no conflict of interest.

Вклад авторов
В написании статьи авторы приняли участие в равных долях.
Contribution of authors
The authors participated in writing the article in equal parts.

Список литературы

1. Чичерин И.В., Федосенков Б.А., Сыркин, И.С., Садовец В.Ю., Дубинкин Д.М. Концепция управления беспилотными транспортными средствами в условиях открытых горных работ. Известия вузов. Горный журнал. 2020;(8):109–120. https://doi.org/10.21440/0536-1028-2020-8-109-120

2. Алешин Б.С., Черноморский А.И., Курис Э.Д. Наземные колесные транспортные модули для решения задач мониторинга окружающей среды горных территорий. Устойчивое развитие горных территорий. 2018;10(4):566–576. https://doi.org/10.21177/1998-4502-2018-10-4-566-576

3. Дубинкин Д.М. Обоснование необходимости создания тяжелых платформ для открытых горных работ. Горное оборудование и электромеханика. 2020;(4):59–64. https://doi.org/10.26730/1816-4528-2020-4-59-64

4. Дубинкин Д.М. Современное состояние техники и технологий в области автономного управления движением транспортных средств угольных карьеров. Горное оборудование и электромеханика. 2019;(6):8–15. https://doi.org/10.26730/1816-4528-2019-6-8-15

5. Voronov Yu., Voronov A., Grishin S., Bujankin A. Increasing the technical level of mining haul trucks. In: Tyulenev M., Zhironkin S., Khoreshok A., Vöth S., Cehlár M., Nuray D. (eds) E3S Web of Conferences. The Second International Innovative Mining Symposium (Devoted to Russian Federation Year of Environment), Kemerovo, November 20–22, 2017. 2017;21:03015. https://doi.org/10.1051/e3sconf/20172103015

6. Naranjo J.E., Clavijo M., Jimenez F., Gomez O., Rivera J.L., Anguita M. Autonomous vehicle for surveillance missions in off-road environment. In: IEEE Intelligent Vehicles Symposium (IV), Gotenburg, Sweden, June 19–22, 2016. P. 98–103. https://doi.org/10.1109/IVS.2016.7535371

7. Nonami K., Kartidjo M., Yoon K.-J., Budiyono A. (eds) Autonomous Control Systems and Vehicles. Intelligent Unmanned Systems. Springer; 2013. 315 p. https://doi.org/10.1007/978-4-431-54276-6

8. Cheng H. Autonomous Intelligent Vehicles. Theory, Algorithms, and Implementation. Springer-Verlag London; 2011. 154 p. https://doi.org/10.1007/978-1-4471-2280-7

9. Taxonomy and Definitions for Terms Related to Driving Automation Systems for OnRoad Motor Vehicles. SAE International in United States; 2016. 30 p. https://doi.org/10.4271/j3016_201609

10. Шадрин С.С. Методология создания систем управления движением автономных колесных транспортных средств, интегрированных в интеллектуальную транспортную среду: дис. … д-ра техн. наук: 05.05.03. М.; 2017. 400 с.

11. Shadrin S.S., Varlamov O.O., Ivanov A.M. Experimental autonomous road vehicle with logical artificial intelligence. Journal of Advanced Transportation. 2017:2492765. https://doi.org/10.1155/2017/2492765

12. Saykin A.M., Buznikov S.E., Karpukhin K.E. The analysis of technical vision problems typical for driverless vehicles. Research Journal of Pharmaceutical, Biological and Chemical Sciences. 2016;7(4):2053–2059. Available at: http://www.rjpbcs.com/pdf/2016_7(4)/[263].pdf

13. Mallat S. A wavelet tour of signal processing. 2nd ed. Academic Press, Springer; 1999. 664 p. Available at: https://www.elsevier.com/books/a-wavelet-tour-of-signal-processing/mallat/978-0-12-466606-1

14. Добеши И. Десять лекций по вейвлетам. Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. 464 с.

15. Auger F., Chassande-Mottin E. Quadratic time-frequency analysis I: Cohen’s class. In: Timefrequency analysis: concepts and methods. ISTE; 2008. P. 131–163.

16. Fedosenkov D.B., Simikova A.A., Kulakov S.M., Fedosenkov B.A. Cohen's class time-frequency distributions for measurement signals as a means of monitoring technological processes. Steel in Translation. 2019;49(4):252–256. https://doi.org/10.3103/S0967091219040065

17. Debnath L. Recent Developments in the Wigner-Ville Distribution and Time-Frequency Signal Analysis. PINSA. 2002;68(1):35–36.

18. Федосенков Б.А., Федосенков Д.В. Автоматизированное управление смесеприготовительными процессами в вейвлет-среде. Кемерово: Кемеровский технологический институт пищевой промышленности; 2015. 188 с.

19. Mallat S, Zhang Z. Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing. 1993;41(12):3397– 3415. https://doi.org/10.1109/78.258082

20. Boashash B., Touati S., Auger F., Flandrin P., Chassande-Mottin E., Stanković L.J. et al. Measures, performance assessment, and enhancement TFDs. In: Boashash B. (ed.) Time-Frequency Signal Analysis and Processing. 2nd ed. Academic Press, Elsevier; 2016. Chapter 7, pp. 387–452. https://doi.org/10.1016/B978-0-12-398499-9.00007-8

21. Townsend S., Lee B. Sparse approximation and atomic decomposition: Considering atom interactions in evaluating and building signal representations. Dissertation … PhD. 2009. 260 p.

22. Федосенков Д.Б., Симикова А.А., Федосенков Б.А. Синтез системы модального управления блоком дозирующих устройств. В: Жуков И.А. (ред.) Машиностроение: инновационные аспекты развития: материалы 2-й международной научно-практической конференции, Санкт-Петербург, 15 марта 2019 г. СПб.: СПбФ НИЦ МС; 2019. С. 162–166. https://doi.org/10.26160/2618-6810-2019-2-162-166