Закономерности формирования напряженного состояния горных пород в кровле выработанного пространства при его развитии
 В.Н. Захаров, В.А. Трофимов, А.В. Шляпин
В.Н. Захаров, В.А. Трофимов, А.В. Шляпин
Институт проблем комплексного освоения недр им. академика Н.В. Мельникова Российской академии наук, г. Москва, Российская Федерация
Горная Промышленность №6 / 2021 стр. 68-75
Резюме: Формирование напряженно-деформированного состояния массива горных пород в кровле отрабатываемого угольного пласта зависит от развития выработанного пространства. При этом считается, что угольный пласт расположен достаточно глубоко и можно полагать, что влиянием дневной поверхности на его состояние можно пренебречь. В этом случае решение строится в рамках аналитического подхода с использованием методов теории функции комплексного переменного и сводится к построению единственной разрешающей аналитической функции. Рассмотрено развитие деформационного процесса формирования выработанного пространства при наличии труднообрушаемой, упругой кровли, которая имеет возможность со временем плавно, без внезапных посадок опускаться на почву. Особое внимание обращается на стадию взаимного касания кровли и почвы, т.е. ее посадки, начиная от первого касания и до полной посадки. При этом формируются два участка зависания кровли, постепенно сокращающихся по протяженности при увеличении размера выработанного пространства. Участок посадки кровли постепенно увеличивается, и вертикальные сжимающие напряжения на контакте постепенно возрастают, стремясь к исходному вертикальному давлению на глубине пласта до начала его отработки. Выявлены зоны растяжения относительно горизонтальных и вертикальных напряжений, приуроченные к участкам зависания кровли, которые могут определять местоположение зон повышенной проницаемости для фильтрации метана и пластовой воды как в породах междупластья, так и в угольном пласте.
Ключевые слова: угольный пласт, выработанное пространство, напряжения, деформации, фильтрация метана, проницаемость, теория функции комплексного переменного, посадка кровли, полная посадка кровли
Благодарности: Исследование выполнено при поддержке Министерства науки и высшего образования Российской Федерации (соглашение №075-15-2021-943) и European Commission Research Fund for Coal and Steel (RFCS) funded project “Advanced methane drainage strategy employing underground directional drilling technology for major risk prevention and greenhouse gases emission mitigation” (GA: 847338 — DD-MET — RFCS-2018/RFCS-2018).
Для цитирования: Захаров В.Н., Трофимов В.А., Шляпин А.В. Закономерности формирования напряженного состояния горных пород в кровле выработанного пространства при его развитии. Горная промышленность. 2021;(6):68–75. DOI: 10.30686/1609-9192-2021-6-68-75.
Информация о статье
Поступила в редакцию: 15.10.2021
Поступила после рецензирования: 30.11.2021
Принята к публикации: 01.12.2021
Информация об авторах
Захаров Валерий Николаевич – член-корреспондент РАН, доктор технических наук, профессор, директор, Институт проблем комплексного освоения недр им. академика Н.В. Мельникова Российской академии наук, г. Москва, Российская Федерация; ORCID: https://orcid.org/0000-0002-9309-2391
Трофимов Виталий Александрович – доктор технических наук, заведующий лабораторией, главный научный сотрудник, Институт проблем комплексного освоения недр им. академика Н.В. Мельникова Российской академии наук, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Шляпин Алексей Владимирович – кандидат технических наук, заместитель директора по научной работе, Институт проблем комплексного освоения недр им. академика Н.В. Мельникова Российской академии наук, г. Москва, Российская Федерация; ORCID: https://orcid.org/0000-0002-9442-0983
Введение
В современных условиях работы высокопроизводительных шахт в связи с резким увеличением протяженности и темпов подвигания очистных забоев заметно возрастают геодинамическая активность массивов горных пород и риски возникновения опасных, в том числе катастрофических газодинамических явлений. Выделяющийся в горные выработки при добыче угля метан является источником возникновения техногенных аварий, сопровождающихся остановкой предприятия, утратой дорогостоящего оборудования и человеческими жертвами, что в совокупности приводит к значительным экономическим потерям для горнодобывающей отрасли РФ. Резонансные аварии на угольных шахтах Российской Федерации в XXI в., имевшие катастрофический характер, произошли именно по причине взрывов метана и угольной пыли.
Отметим, что основным мероприятием по удалению метана из выработок является их проветривание, которое, однако, ограничено максимальной допустимой скоростью потока воздуха по выработкам. В связи с этим важным становится заблаговременное удаление метана из угольного пласта и вмещающих пород с целью уменьшения его выделения в процессе очистных работ в выработки через стенки, в частности, в забое, а также непосредственно из отбитого угля.
Для этой цели служат дегазационные скважины, которые организованы в систему, пронизывающую угольный пласт на разных уровнях и по разным направлениям. В настоящее время существует большое разнообразие тем или иным способом обоснованных способов расположения таких скважин, основанных по большей части на экспериментальных представлениях об их функционировании.
Несомненно, что в основу системы дегазации должен быть положен подход, основанный на анализе состояния угольного пласта и вмещающих пород и позволяющий оценить возможные газовые потоки в углепородном массиве. Определяющим параметром при этом является проницаемость массива, включая угольный пласт, зависящая от количества сорбированного углем метана и его нагруженности, т.е. напряженно-деформированного состояния.
Анализу напряженного состояния налегающего массива горных пород посвящены многочисленные исследования, выполненные с использованием различных подходов, включая эксперименты на эквивалентных материалах и в натурных условиях [1–8]. Несомненные успехи в решении задач, связанных с описанием развития деформационных процессов в массиве с многочисленными пластами по мере их отработки, были достигнуты с применением различных численных алгоритмов [9–12]. Однако применение таких алгоритмов не позволяет легко построить конечные, инженерные соотношения, в простой форме описывающие поведение массива. Для этого необходимо проведение многочисленных численных расчетов с варьируемыми параметрами с последующим обобщением полученного набора результатов. В связи с этим роль аналитических подходов к решению геомеханических задач становится значимой.
Очевидно, напряженное состояние массива в первую очередь зависит от размеров выработанного пространства, и по мере их увеличения претерпевает несколько характерных переходов в зависимости от «эффективной» мощности вынимаемого пласта. Для первого этапа отработки пласта характерно зависание основной кровли. При этом не будем рассматривать особенности деформирования и обрушения ложной и непосредственной кровли, т.е. будем считать, что их фактически нет, и всё определяет основная кровля, которая плавно опускается по мере развития очистных работ.
Напряженно-деформированное состояние массива для подобных пластовых систем может быть описано аналитически в рамках теории функций комплексного переменного [13]. Такой подход ограничен достаточно узким кругом решаемых задач, но там, где он применим, могут быть получены конечные соотношения, описывающие моделируемые процессы. В частности, распределения по пространству напряжений, деформаций, смещений, проницаемости и др.
Таким образом, на первом этапе кровля опускается, и почва поднимается, но их сближения недостаточно, чтобы они вошли в контакт.
Второй этап деформирования начинается с момента касания почвы и кровли, что приводит к существенному изменению характера деформирования массива со своими закономерностями.
По мере развития выработанного пространства зона контакта кровли и почвы постепенно увеличивается и при достижении определенного размера стабилизируется. При этом состояние участка массива, примыкающего к забою лавы, становится неизменным. Фактически это означает, что произошла полная посадка кровли и в центральной части выработанного пространства восстановилось исходное напряженное состояние массива до проведения выработок [14].
Исходя из сказанного целью настоящего исследования можно полагать теоретическое описание деформационных процессов в кровле выработанного пространства и получение конечных соотношений, описывающих перераспределение напряжений в зонах возможной повышенной проницаемости углепородного массива. Такого рода соотношения предпочтительны при формулировке и решении задач массопереноса в сравнении с табличным заданием параметров, получаемых при численном решении.
Общая постановка задачи
оценки напряженно-деформированного состояния массива при развитии выработанного пространства Развитие выработанного пространства при отработке пластового месторождения будем связывать с непрерывным возрастанием его общей протяженности, т.е. величины Lв, начиная фактически от нуля и до сколь угодно больших значений, ограниченных принятой системой разработки. Для упрощения постановки задачи и получения решения будем считать, что очистные работы развиваются симметрично относительно вертикальной оси 0y, и, следовательно, во многих задачах можно ограничиться рассмотрением решения только для положительных значений x, т.е. в области x > 0, y > 0. В этом случае удобно полагать Lв= 2L, где L – полупролет выработанного пространства.
Рассмотрим основные закономерности и характерные особенности перераспределения напряжений в массиве для трех типичных этапов, схематически изображенных на рис. 1, в своей совокупности полностью охватывающих развитие выработанного пространства [14].
Первый этап (рис. 1, а) отражает развитие выработанного пространства, при котором сближение боковых пород всюду меньше эффективной мощности тэ разрабатываемой залежи. При увеличении протяженности выработанного пространства, т.е. величины L, увеличиваются прогиб кровли и поднятие почвы, т.е. происходит постепенное сближение боковых пород. Очевидно, что протяженность L ограничена предельным значением L0 [14], при котором максимальное сближение боковых пород равно mэ.
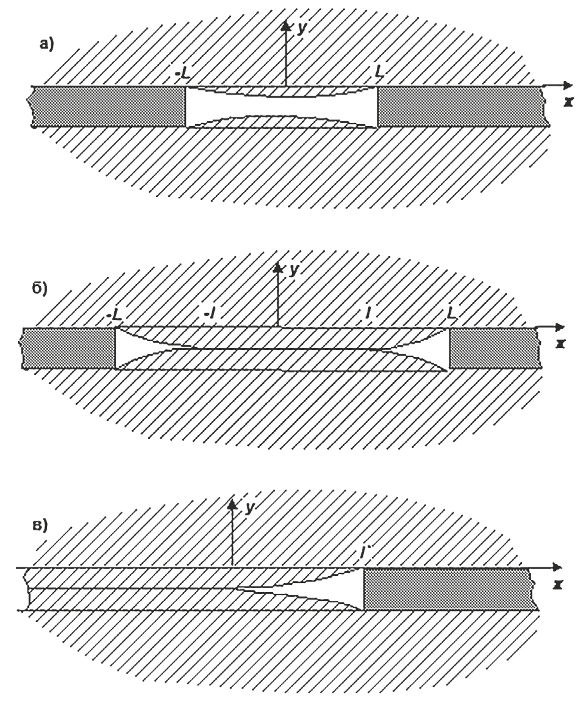
- Рис. 1 Различные стадии развития выработанного пространства
- Fig. 1 Different stages in development of mined-out space
Использование величины mэ вместо реальной мощности пласта m связано с тем, что породы непосредственной кровли, как правило, обрушаются в выработку, и при этом происходит их разрыхление. При посадке кровли на обрушенные породы происходит их постепенное сжатие, но они не могут уплотниться до исходного состояния даже при полной посадке кровли. В связи с этим пласт обладает некоторой фиктивной, кажущейся мощностью mэ, для которой всегда mэ > m
На рис. 1, б отражено дальнейшее развитие выработанного пространства при L > L0, характерной особенностью которого является наличие участка силового взаимодействия боковых пород протяженностью 2l, который непрерывно увеличивается по мере развития выработанного пространства. На этом участке сближение боковых пород равно mэ, а на его продолжении с обеих сторон сохраняются открытые выработанные пространства каждое протяженностью L-l. Когда участок силового взаимодействия становится достаточно большим по сравнению с L-l, открытые выработанные пространства практически не оказывают взаимного влияния друг на друга, и напряженное состояние массива вблизи границы x = L уже фактически не зависит от дальнейшего продвижения этой границы, т.е. от величины L. Очевидно, что в этом случае отсутствует симметрия, и задача должна быть поставлена для всей полуплоскости y > 0. Такая конфигурация свободного выработанного пространства отражена на рис. 1, в.
Далее рассмотрим более подробно и детально основные закономерности и характерные особенности перераспределения напряжений вокруг протяженных выработок для этапа развития очистных горных работ, как это отражено на рис. 1, б, когда кровля и почва находятся в контакте.
Как уже сказано выше, решение задач о перераспределении напряжений и смещений в массиве горных пород вследствие образования и развития поземных выработок будем рассматривать в рамках аналитического подхода с использованием функций комплексного переменного.
В этом случае для построения решения используются одна или две разрешающие аналитические функции комплексного переменного (в зависимости от симметрии рассматриваемой задачи). При решении задач для случая отработки горизонтального пласта в соотношения для напряжений и смещений входит единственная функция, вид которой зависит от стадии развития горных работ и размеров выработанного пространства (см. рис. 1).
Напряженное состояние горных пород в случае силового взаимодействия пород кровли и почвы при ее посадке. Общее решение
Более тщательное рассмотрение варианта с посадкой кровли может быть оправдано тем, что в настоящее время во многих случаях при отработке угольных пластов применяется вариант системы отработки длинными угольными столбами с использованием длинных забоев, когда линейные размеры выработанного пространства достигают сотен метров. Даже для достаточно мощных угольных пластов в этом случае плавное оседание налегающего массива при наличии прочной, упругой основной кровли, достаточно велико для образования контакта кровли и почвы. В силу сказанного рассмотрение такой ситуации имеет несомненный интерес.
В случае, показанном на рис. 1, б, т.е. когда L > L0 и ширина центральной части отработанного участка, на котором кровля плавно опустилась на почву, равна 2l, разрешающая функция Ф(z) имеет вид [14]
![разрешающая функция Ф(z) имеет вид [14]](/images/2021/06_2021/068_f1.jpg) , (1)
, (1)
где H – глубина залегания пласта, γ – средний удельный вес пород кровли, z = x + iy.
При этом размер зоны посадки кровли l связан с L уравнением
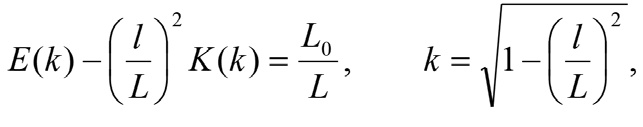 (2)
(2)
где K(k), E(k) – полные эллиптические интегралы первого и второго рода [15].
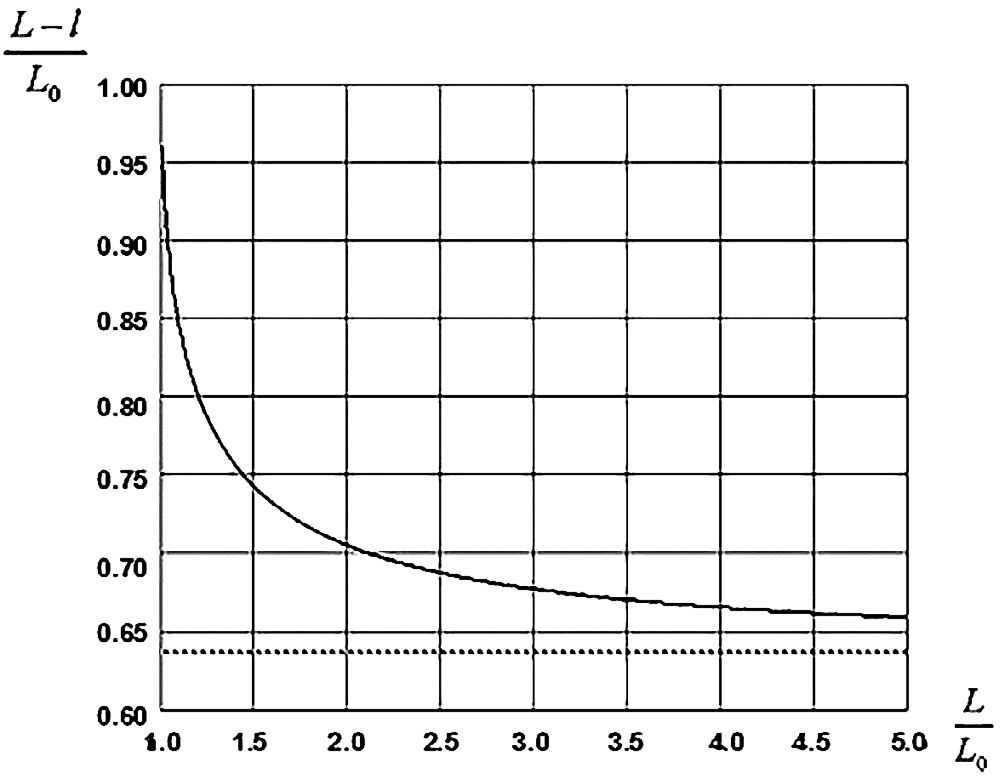
- Рис. 2 Взаимосвязь относительной ширины зависающей части кровли от относительной ширины отработанного участка пласта
- Fig. 2 Correlation between the relative width of the hanging part of the roof and the relative width of the minedout section of the formation
Графически эта связь в виде зависимости относительной ширины зависающей части кровли (L-l)/L0 от относительной ширины отработанного участка пласта L/L0 показана на рис. 2. С увеличением L увеличивается l, но (L-l)/L0 убывает от 1 до 2/π, т.е.
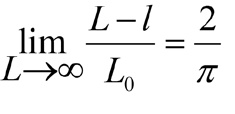 (3)
(3)
Напряжения вокруг всего выработанного участка определяются согласно [13; 14] с учетом (1) по формулам
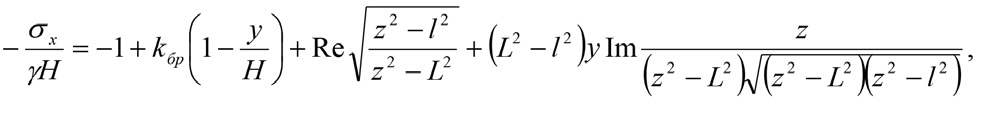 (4)
(4)
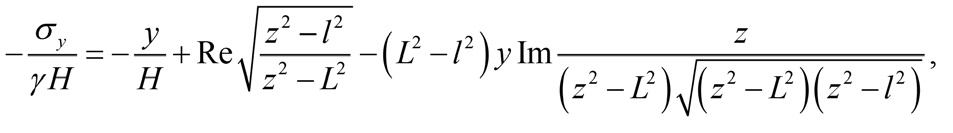 (5)
(5)
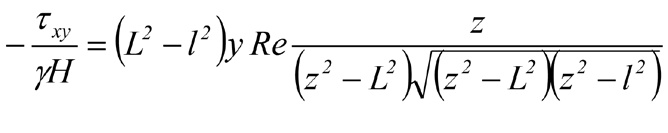 , (6)
, (6)
где σx, σy, τxy – горизонтальное и вертикальное нормальные напряжения, касательное напряжение в кровле, kбр– коэффициент бокового распора.
При коэффициенте бокового распора kбр ≥ 1 горизонтальные напряжения σx над выработкой и под ней всюду сжимающие. При kбр ˂ 1 в кровле выработки возникают зоны горизонтальных растягивающих напряжений. На свободной поверхности кровли и почвы они максимальны и сохраняют свое постоянное значение независимо от протяженности выработки L, т.е.
![]() , (7)
, (7)
С увеличением расстояния от этих поверхностей вглубь горного массива растягивающие напряжения σx убывают до нуля, а за пределами границы σx = 0, которая определяется из (4), горизонтальные напряжения всюду сжимающие. Таким образом, зона растягивающих горизонтальных напряжений в массиве горных пород приурочена к кровле выработанного пространства, где она возникает при малых горизонтальных исходных напряжениях, т.е. при kбр ˂ 1.
Обсуждение результатов. Распределение горизонтальных напряжений в кровле пласта
Рассмотрим более детально распределение горизонтальных напряжений σ x непосредственно в кровле пласта, т.е. при y = 0. Из (4) следует
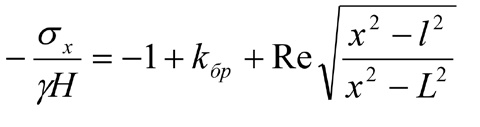 , (8)
, (8)
Очевидно, что на отрезке l < x < L будет 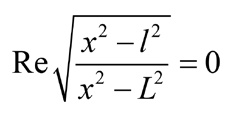 , а вне этого отрезка
, а вне этого отрезка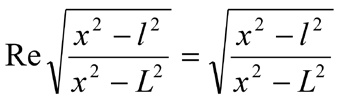
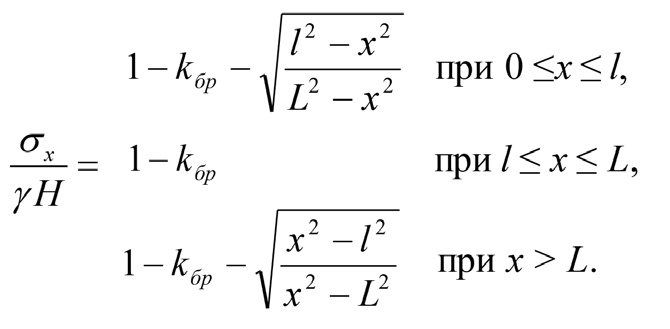 , (9)
, (9)
Таким образом, В качестве примера на рис. 3 показано распределение горизонтальных напряжений σx при L/L0 = 2.5 kбр = 0.6. При x = 0 из (9) имеем
![]() , (10)
, (10)
В этом случае l/L0 = 1.81 и l/L = 0.724, т.е. -0.324.
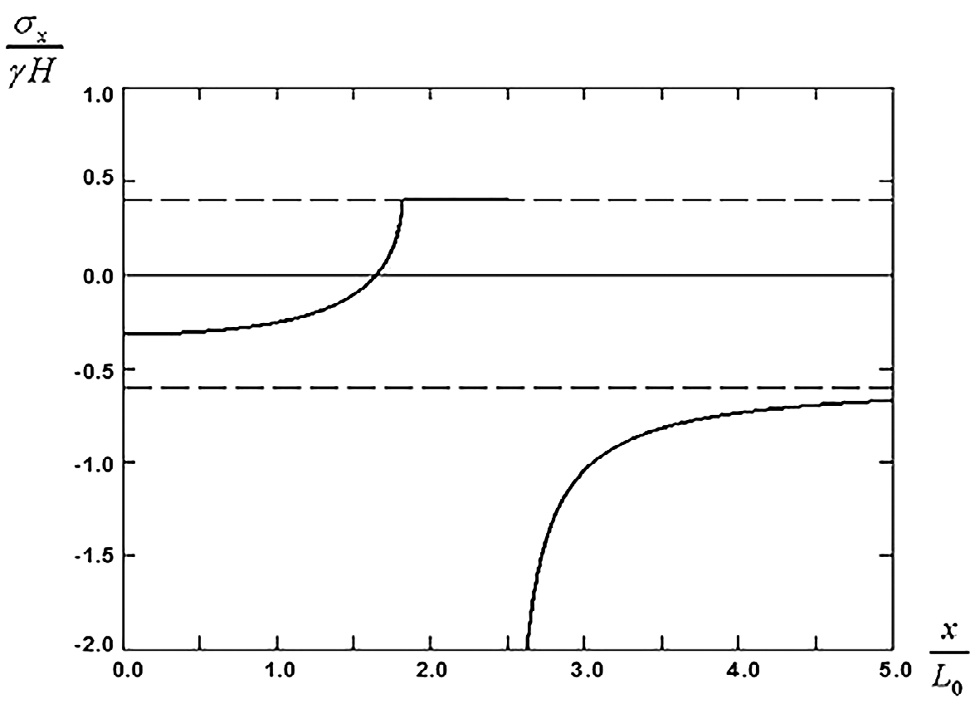
- Рис. 3 Распределение горизонтальных напряжений на поверхности кровли
- Fig. 3 Distribution of horizontal stresses on the roof surface
При развитии выработанного пространства, т.е. при росте L, одновременно растет и l, а также и их отношение от 0 при L = L0 до 1 при L→∞. Таким образом, при заданном kбр величина (σx / γН)|х=0 постепенно уменьшается от 1–kб при L = L0 до kбр– при L→∞, что отражено на рис. 4 для разных kбр.
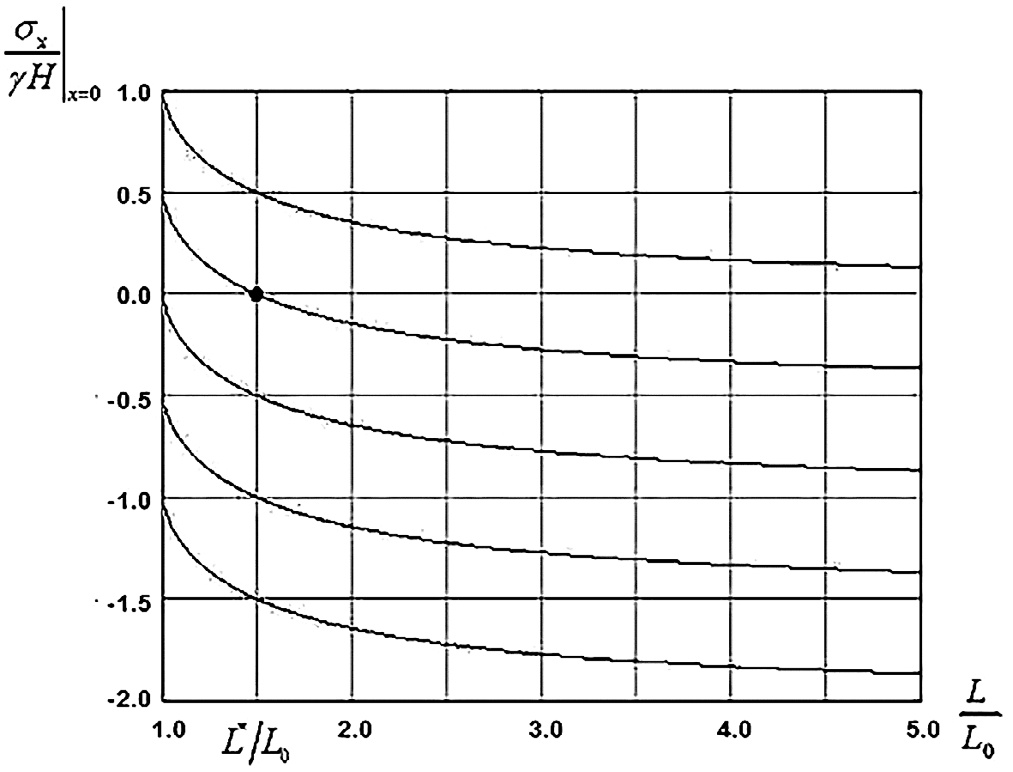
- Рис. 4 Изменение горизонтальных напряжений в центре зоны касания при увеличении выработанного пространства для разных значений коэффициента бокового распора
- Fig. 4 Variation of horizontal stresses in the center of the caving zone while increasing the mined-out space for different values of the horizontal stress coefficient
Из рисунка также видно, что при kбр = 0 в начале координат всегда имеет место растяжение для любых значений L/L0, а при kбр > 1 – сжатие. В промежутке между 0 и 1, т.е. при 0 < kбр < 1, может быть растяжение или сжатие в зависимости от величин kбр и L/L0. При этом по мере развития выработанного пространства растяжение в точке x = 0 при некотором L* переходит в сжатие.
Положение точки x = L* определяется из первого соотношения (9) при σx = 0. После преобразований получим соотношение
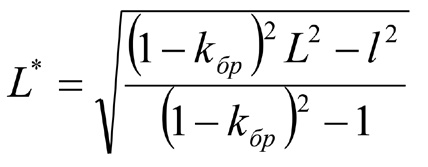 , (11)
, (11)
Ранее было показано [14], что в случае зависающей кровли при 0 < kбр < 1 вне зависимости от L над всем выработанным пространством образуется зона растяжения по σx с максимумом этой величины над серединой выработки.
Когда L становится равным L0, кровля и почва выработки касаются в ее середине, после чего участок касания l постепенно увеличивается по мере роста L. При этом растягивающие напряжения σx в точке x = 0, начиная от момента касания, уменьшаются и при L = L* становятся равными нулю.
После этого в начале координат и в ближайшей окрестности формируется зона сжимающих напряжений σx. То есть зона растяжения для зависающей кровли при L < L0 распадается на две части, связанные с соответствующими участками зависания при L > L0. Из (10) следует, что это происходит при условии l/L=1–kбр. Принимая во внимание (2), можно записать условие распада в виде
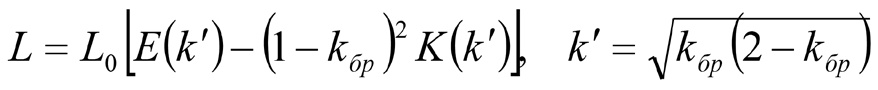 , (12)
, (12)
При этом формируются два симметричных свода над выработанным пространством, в пределах которого имеет место растяжение по x.
Развитие по мере увеличения выработанного пространства этих сводов (правой части) показано на рис. 5 для kбр = 0.6 и H/L = 5. Цифрами обозначена величина L/L0. При достаточно больших L по сравнению с L0 форма контура зоны растягивающих напряжений σx стабилизируются, локализуясь вблизи забоя, x = L, в соответствии с тем, как (L-l)/L0 становится практически равной 2/π.

- Рис. 5 Изменение формы зоны растягивающих горизонтальных напряжений по мере роста протяженности выработанного пространства
- Fig. 5 Changes in the shape of the tensile horizontal stress zone as the length of the mined-out space increases
Очевидно, что протяженность зоны растяжения L-L* несколько больше, чем зоны свободно зависающей кровли L-l, поскольку из (11) следует, что всегда l > L*. Фактически это означает, что горизонтальные напряжения σ x остаются растягивающими над всей зависающей кровлей, где они равны 1–kбр , и над частью зоны касания в промежутке L* < x < l, где они определяются в соответствии с (9).
Заметим, что при L→∞, величина (σx /γН)х=0 → – kбр , как это и следует для ненарушенного выработкой массива. Таким образом, когда забой уходит достаточно далеко, в точке x = 0, y = 0 и близлежащих точках восстанавливаются исходные напряжения.
Обсуждение результатов. Распределение вертикальных напряжений в кровле пласта
Вертикальные растягивающие напряжения σ y всегда возникают в плоской кровле отработанного участка пласта и не зависят от коэффициента бокового распора kбр. На свободной поверхности зависающей кровли они равны нулю, σy = 0. С увеличением расстояния от этой поверхности вглубь массива растягивающие напряжения возрастают до своего максимального значения, а затем убывают до нуля. За пределами границы, которая определяется из соотношения (5) и на которой σy = 0, вертикальные напряжения всюду сжимающие. При возрастании L и достижении им значения L0 соответствующая зона растягивающих σy, в отличие от σx, практически сразу же распадается на две части. Она имеет вид, аналогичный приведенному на рис. 5.
На кровле пласта σy, в соответствии с (5), равны
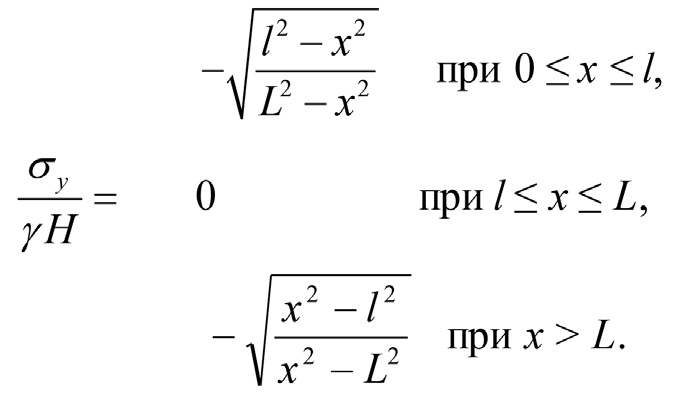 , (13)
, (13)
и при kбр = 1 совпадают с σx (8).
Как и для горизонтальных напряжений, зона растягивающих вертикальных напряжений приурочена к двум участкам зависающей кровли, которые по мере развития работ постепенно уменьшаются. Таким образом, наиболее протяженной зона зависания будет непосредственно перед соприкосновением кровли и почвы, соответственно, и размер зоны растягивающих вертикальных напряжений будет наибольшим, как и величина этих напряжений.
Как те, так и другие напряжения (σx, σy) при x = L имеют особенность, т.е. становятся сколь угодно большими. Вводя переменную δ (расстояние от забоя вглубь пласта) с использованием соотношения х = L + δ , и имея в виду, что δ→0 , для напряжений получим соотношение
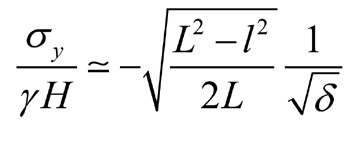 , (14)
, (14)
При l = 0, т.е. для полностью зависающей кровли, будем иметь
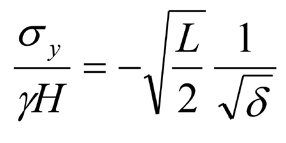 , (15)
, (15)
Обобщая (14), запишем
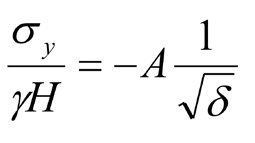 , (16)
, (16)
где A изменяется от ![]() при 0 < L < L0 до
при 0 < L < L0 до ![]() , а затем до
, а затем до 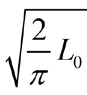 при L→∞, т.е. в случае посадки кровли возрастает от 0.707
при L→∞, т.е. в случае посадки кровли возрастает от 0.707![]() до 0.798
до 0.798![]() .
.
Таким образом, по мере развития выработанного пространства особенность в напряжениях на забое выработки в рассматриваемом случае практически не изменяется, возрастая менее чем на 1.5%.
Заключение
В статье приведены соотношения, в полной мере описывающие напряженно-деформированное состояние массива горных пород на этапе плавной посадки кровли выработанного пространства при отработке горизонтальной (слабонаклонной) пластовой залежи. На этом этапе происходит взаимное касание кровли и почвы образующегося и постепенно расширяющегося выработанного пространства. Отметим, что до момента касания пролет свободно зависающей кровли постепенно увеличивается и достигает предельной величины L0, определяемой деформационными свойствами пород кровли. При дальнейшем развитии очистных работ этот пролет постепенно сокращается и распределение напряжений вблизи забоя открытого выработанного пространства перестает изменяться.
Таким образом, наиболее опасная с точки зрения возможного обрушения ситуация в массиве возникает в момент достижения протяженности выработанного пространства величины L0, когда размеры зон разгрузки достигают наибольших размеров, а значения растягивающих напряжений в них наибольшие.
С другой стороны, в этом случае происходит наибольшее расслоение пород и возрастает их проницаемость, что способствует выходу метана и дегазации углепородного массива. Очевидно, что такая дегазация будет неоднородна по массиву и в основном приурочена к центральной части выработанного пространства. При этом следует иметь в виду тот факт, что выработанное пространство постепенно расширяется, и его центральная часть перемещается со временем в направлении развития работ [16–18].
В рассматриваемой ситуации состояние массива описывается при помощи одной функции комплексного переменного, которая и определяет все особенности распределения напряжений и смещений во вмещающем массиве горных пород.
Показано, что в массиве существуют зоны разгрузки, в которых напряжения меньше тех, что были до начала работ. Интересно, что в кровле выработанного пространства всегда есть зона растягивающих вертикальных напряжений, способствующих расслоению пород кровли.
Существуют также зоны пригрузки с повышенными напряжениями. В частности, для вертикальных напряжений это краевая часть пласта, где в рамках используемой постановки задачи наблюдаются особенности, т.е. напряжения становятся бесконечными.
Полученные результаты предназначены для использования при постановке и решении задач массопереноса флюидов в углепородном массиве при его разгрузке горными работами и дегазацией. С использованием соответствующих взаимосвязей проницаемости и напряженного состояния массива полученные соотношения для распределения напряжений позволят построить зоны распределения наведенной проницаемости с возможностью ее вычисления в произвольной точке зоны фильтрации.
Список литературы
1. Feng D., Biao L., Nuwen X., Yongguo Z. Microseismic early warning of surrounding rock mass deformation in the underground powerhouse of the Houziyan hydropower station. Tunnelling and Underground Space Technology. 2017;62:64–74. https://doi.org/10.1016/j.tust.2016.11.009
2. Galvin J.M. Ground engineering – principles and practices for underground coal mining. Springer; 2016. 684 p. https://doi.org/10.1007/978-3-319-25005-2
3. Бедарев Н.Т., Любимов О.В., Бородин И.В., Шайхисламов А.Р. Формирование давления обрушенных пород в выработанном пространстве. В кн.: Пудов Е.Ю., Клаус О.А. (ред.) Перспективы инновационного развития угольных регионов России: сб. тр. 5-й Междунар. науч.-практ. конф., г. Прокопьевск, 30–31 марта 2016 г. Прокопьевск: Кузбасский государственный технический университет имени Т.Ф. Горбачева; 2016. С. 126–127.
4. Семенцов В.В., Осминин Д.В., Нифанов Е.В. Устойчивость выемочных горных выработок при отработке пластов с труднообрушающимися кровлями. Вестник Научного центра ВОСТНИИ по промышленной и экологической безопасности. 2021;(3):14– 25. https://doi.org/10.25558/VOSTNII.2021.47.12.002
5. Шванкин М.В., Бондарев А.В. Особенности отработки удароопасных пластов в условиях труднообрушаемых кровель. Вестник Научного центра ВОСТНИИ по промышленной и экологической безопасности. 2019;(2):81–88. https://doi.org/10.25558/VOSTNII.2019.10.2.010
6. Зуев Б.Ю. Динамика изменения напряжений в труднообрушающейся кровле и в опорной зоне в ходе эволюции структурных параметров массива при вторичных осадках. Записки горного института. 2012;199:168–172. Режим доступа: https://pmi.spmi.ru/index.php/pmi/article/view/5838
7. Игнатов Е.В. Зависимости и особенности смещений и формирования зон разрушения кровли и краевой части пласта при взаимодействии с элементной базой бесцеликовой технологии. Техника и технология горного дела. 2020;(4):4–41. https://doi.org/10.26730/2618-7434-2020-4-4-41
8. Лобков Н.И., Клочко И.И. Формирование области сдвижения пород кровли при ведении очистных работ. Проблемы горного давления. 2016;(4):61–68. Режим доступа: http://www.pgd.donntu.org/images/archive/31/05_lobkov.pdf
9. Yang J.H., Yao C., Jiang Q.H., Lu W.B., Jiang S.H. 2D numerical analysis of rock damage induced by dynamic in-situ stress redistribution and blast loading in underground blasting excavation. Tunnelling and Underground Space Technology. 2017;70:221–232. https://doi.org/10.1016/j.tust.2017.08.007
10. Lubosik Z., Waclawik P., Horak P., Wrana The influence of in-situ rock mass stress conditions on deformation and load of gateroad supports in hard coal mine. Procedia Engineering. 2017;191:975–983. https://doi.org/10.1016/j.proeng.2017.05.269
11. Waclawik P., Kukutsch R., Konicek P., Ptacek J., Kajzar V., Nemcik J., et al. Stress state monitoring in the surroundings of the roadway ahead of longwall mining. Procedia Engineering. 2017;191:560–567. https://doi.org/10.1016/j.proeng.2017.05.218
12. Курленя М.В., Миренков В.Е. Деформирование весомого массива горных пород в окрестности прямолинейной конечной трещины. Физико-технические проблемы разработки полезных ископаемых. 2018;(6):14–20. https://doi.org/10.15372/FTPRPI20180602
13. Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. Основные уравнения, плоская задача, кручение и изгиб. М.: Наука; 1966. 708 с.
14. Кузнецов С.В. Общие закономерности и характерные особенности перераспределения напряжений в массивах горных пород при развитии выработанного пространства. Физико-технические проблемы разработки полезных ископаемых. 1988;(6):3–16.
15. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Госиздат физ.-мат. лит.; 1963.
16. Zakharov V.N., Malinnikova O.N., Trofimov V.A., Filippov Yu.A. Effect of gas content and actual stresses on coalbed permeability. Journal of Mining Science. 2016;52( 2):218–225. https://doi.org/10.1134/S1062739116020345
17. Трофимов В.А., Филиппов Ю.А. Особенности формирования массопереноса метана в породах междупластья. Оборудование и технологии для нефтегазового комплекса. 2021;(3):71–78. https://doi.org/10.33285/1999-6934-2021-3(123)-71-78
18. Захаров В.Н., Шляпин А.В., Трофимов В.А., Филиппов Ю.А. Изменение напряженно-деформированного состояния углепородного массива при отработке угольного пласта. Горный информационно-аналитический бюллетень. 2020;(9):5–24. https://doi.org/10.25018/0236-1493-2020-9-0-5-24







