Применение цифровых двойников для прогнозной оценки удароопасности надштрековых целиков

Н.Е. Мороз¹, Д.В. Сидоров², М.А. Соннов^3
1 АО «ВНИМИ», г. Санкт-Петербург, Российская Федерация
² ООО «Полигор», г. Санкт-Петербург, Российская Федерация
³ ООО «Фидесис», г. Москва, Российская Федерация
Горная Промышленность №3 / 2022 стр. 93-98

Резюме: Надштрековые целики применяют для защиты транспортных горных выработок от воздействия горного давления и попадания в них обрушенной горной массы. В то же время оставление целиков, сложенных хрупкими рудами, в условиях влияния значительных сжимающих напряжений представляет опасность по возможному проявлению горного давления в динамической форме. Из-за конструктивных особенностей систем разработки и требований правил безопасности доступ к надштрековому целику со стороны восстания не представляется возможным, что ограничивает возможность выполнения полноценного инструментального прогноза удароопасности. В этой связи для прогнозной оценки удароопасности надштрековых целиков целесообразно использовать цифровые двойники. В статье приводится опыт института ВНИМИ по применению специализированного программного обеспечения «PRESS 3D URAL» (ООО «Полигор», г. Санкт-Петербург) и «FIDESYS» (ООО «Фидесис», г. Москва) для комплексной оценки напряженно-деформированного и удароопасного состояния надштрекового целика. На первом этапе выполнена численная оценка природно-тектонического поля напряжений с применением программного обеспечения «PRESS 3D URAL». На втором этапе с применением «FIDESYS» выполнена оценка техногенного напряженно-деформированного состояния массива горных пород и рудного надштрекового целика при подземной отработке запасов камерной системой разработки. На заключительном этапе с использованием данных о прочностных свойствах руд выполнена прогнозная оценка удароопасности рудного целика.

Ключевые слова: надштрековые целики, горное давление, тектоническое строение, численное моделирование, метод граничных интегральных уравнений, метод конечных элементов, коэффициент бокового отпора, прогноз удароопасности

Благодарности: Исследование выполнено при финансовой поддержке РФФИ и Министерства культуры, образования, науки и спорта Монголии в рамках научного проекта № 19-510-44013\21

Для цитирования: Мороз Н.Е., Сидоров Д.В., Соннов М.А. Применение цифровых двойников для прогнозной оценки удароопасности надштрековых целиков. Горная промышленность. 2022;(3):93–98. https://doi.org/10.30686/1609-9192-2022-3-93-98

Информация о статье

Поступила в редакцию: 02.06.2022

Поступила после рецензирования: 20.06.2022

Принята к публикации: 21.06.2022

Информация об авторах

Мороз Никита Евгеньевич – научный сотрудник, АО «ВНИМИ», г. Санкт-Петербург, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Сидоров Дмитрий Владимирович – доктор технических наук, действительный член АГН России, заместитель генерального директора по научной работе, ООО «Полигор», г. Санкт-Петербург, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Соннов Максим Александрович – действительный член АГН России, заместитель генерального директора по продажам, ООО «Фидесис», г. Москва, Российская Федерация

Введение

Надштрековый целик является одним из основных элементов систем разработки с открытым очистным пространством, поскольку связывает очистные и откаточные горные работы, защищает транспортные выработки от негативного воздействия горного давления, возникающего в процессе ведения очистных работ.

В ситуациях, когда целики сложены хрупкими рудами и породами, они представляют опасность по возможному проявлению горного давления в динамической форме. Согласно п. 150 Правил безопасности при ведении горных работ и переработке твердых полезных ископаемых: федеральные нормы и правила в области промышленной безопасности¹ (далее – Правила безопасности), доступ к надштрековому целику со стороны восстания не представляется возможным, что ограничивает возможность выполнения полноценного инструментального прогноза удароопасности.

Для решения данной проблемы целесообразно использовать цифровые двойники. Для прогноза удароопасности рудных целиков, формируемых в блочном массиве, реализуется концепция «блочный массив – добычной участок – рудный целик». Текущий уровень развития науки и техники позволяет создавать математические и компьютерные модели, описывающие с высокой степенью адекватности поведение блочного массива горных пород при подземной отработке рудных месторождений, в том числе в удароопасных условиях [1–5]. На первом этапе реализации концепции выполнена численная оценка природно-тектонического поля напряжений с применением ПО «PRESS 3D URAL» [6]. На втором этапе с применением ПО «FIDESYS» выполнена оценка техногенного напряженно-деформированного состояния массива горных пород и рудного надштрекового целика при подземной отработке запасов камерной системой разработки [7–8]. На заключительном этапе с использованием данных о прочностных свойствах руд выполняется прогнозная оценка удароопасности рудного целика [9]. Предложенный механизм прогноза удароопасности позволяет выполнять проверку соответствия размеров целика уровню действующих напряжений, обеспечивать безопасность и экономическую эффективность горных работ путем оперативной адаптации к изменяющимся геологическим и геомеханическим условиям, что является приоритетом горнодобывающих предприятий [10].

Оценка природно-тектонического поля напряжений с применением ПО «PRESS 3D URAL»

Программное обеспечение PRESS 3D URAL широко апробировано для геодинамического районирования рудных месторождений, разрабатываемых крупнейшими Российскими горнодобывающими компаниями – ПАО «ГМК «Норильский никель»», АО «Севуралбокситруда», АО «Апатит», АО «Воркутауголь» и др.

Средством выделения тектонически-напряженных зон являются аналитические методы расчета напряженного состояния блочного массива горных пород. Основная особенность задач о системах взаимодействующих блоков состоит в том, что число границ (контактов) существенно больше, чем в обычных задачах, решаемых численными методами. Поэтому целесообразно использовать программные комплексы, базирующиеся на методе граничных интегральных уравнений или методах вычислений, которые наилучшим образом приспособлены к учету большого количества границ.

Наличие тектонических разрывов, разделяющих горный массив на блоки, означает нарушение непрерывности поля напряжений в блочном массиве и разделение его на участки, состоящие из одного или нескольких блоков с более или менее однородным уровнем напряженности для данного ранга блоков [11–13].

Чтобы вычислить напряжения Ρ_i, возникающие в ненарушенном массиве горных пород от воздействия тектонических нарушений, необходимо ввести информацию, характеризующую горно-геологические условия рассматриваемой обстановки.

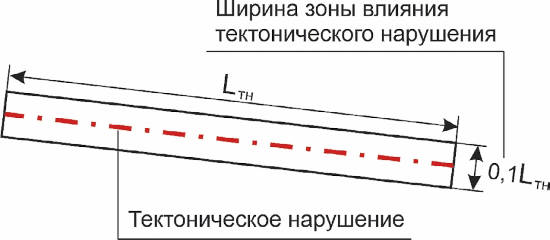Рис. 1 Схема к определению ширины зоны тектонической нарушенности Fig. 1 Schematic drawing for determining the width of a tectonic fault zone

Входная информация условно разделена на две части. На первом этапе задается информация, необходимая для учета геометрических размеров граничных элементов, принадлежащих как к массиву горных пород, так и к зонам тектонических нарушений (рис. 1). На втором этапе для каждого из сформированных граничных элементов горного массива задается следующая информация: коэффициент Пуассона, модуль упругости и мощность. В расчетных элементах, принадлежащих зонам тектонических нарушений, формируются граничные условия в виде коэффициентов концентрации дополнительных напряжений q_z. При неизученном и слабоизученном состоянии горных пород в зонах тектонических нарушений для расчетов необходимо принимать наихудший случай q_z =0,5. По мере уточнения характеристики тектонической структуры при разработке месторождения параметр q_z подлежит корректировке.

Основным результатом численных экспериментов являются величины широтной и меридиональной тектонических составляющих, действующих в ненарушенных граничных элементах массива горных пород.

Рис. 2 Определение исходного поля напряжений в ПО «Press 3D UraL» а – разбиение линеаментов с расчетом длины между узлами; б – построение ширины влияния каждого линеамента; в – формирование расчетной блочной модели участка; г – формирование расчетной геомеханической модели участка; д – результаты расчета тектонической составляющей в долях γН, ♦ – предполагаемая зона влияния тектонических нарушений; е – распределение широтной тектонической составляющей в долях γН (по х); ж – распределение меридиональной тектонической составляющей в долях γН (по y); з – распределение наибольшей тектонической составляющей в долях γН

Fig. 2 Defining the initial stress field in the Press 3D UraL software а – dividing the lineaments with the length calculation between the nodes; б – plotting the impact width of each lineament; в – generating a computational block model of the site; г – generating a computational geomechanical model of the site; д) results of calculating the tectonic component in fractions γН, ♦ – assumed impact zone of tectonic faults; е) distribution of the latitudinal tectonic component in fractions γН (х axis); ж – distribution of the meridional tectonic component in fractions γН (y axis); з – distribution of the maximum tectonic component in fractions γН

На рис. 2 представлены этапы формирования тектонической схемы для моделирования и процесс моделирования, результаты которого свидетельствуют о формировании гравитационно-тектонического поля напряжений в границах рассматриваемого месторождения. Несмотря на превышение полученной тектонической составляющей относительно распределения по Диннику, максимальным напряжением является вертикальное σmax= γH Величина горизонтальных напряжений на различных участках месторождения изменяется от 0,3 γH (вне зон влияния тектонических нарушений, внутри блоков) до 1,0 γH (вблизи узлов сопряжения и зон влияния тектонических нарушений, на границах блоков).

Оценка техногенного напряженно-деформированного состояния с применением ПО «FIDESYS»

После определения напряженного состояния нетронутого массива горных пород совершается переход к расчетам техногенных полей напряжений, которые будут в различной степени проявляться во время отработки месторождения полезных ископаемых.

Как уже было сказано, метод ГИУ позволяет просчитать горные отводы площадью в десятки квадратных километров с расчетными элементами порядка 20 на 20 м. В свою очередь, для анализа состояния рудных целиков, породного массива вокруг очистных пространств и горных выработок необходима более детальная расчетная единица, порядка 0,1 м, которую успешно реализовывает метод конечных элементов, в частности, в программном комплексе CAE FIDESYS.

Постановка задачи в данной статье аналогична моделированию, освещенному в работе [9].

В расчетной области заданы граничные условия на рёбрах: нижнее ребро u_y = 0; левое ребро u_x = 0; правое ребро u_x = λ_т * (H – y) * p * (–g), где λ_т – коэффициент бокового отпора; H – высота расчётной модели; y – координата по оси y; p – плотность пород; g – ускорение свободного падения.

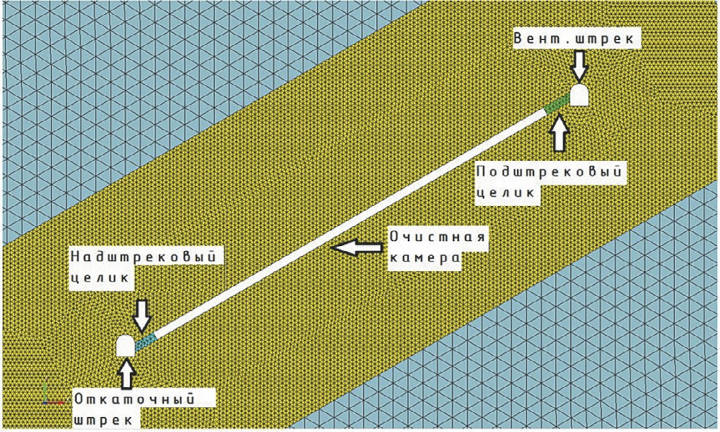Рис. 3 Моделирование НДС массива при разработке маломощных рудных тел камерной системой (m_норм= 2 м; L_кам= 90 м)

Fig. 3 Modelling of the stress-andstrain state of the rock mass in mining narrow vein orebodies using the headingand- stall method (m_norm= 2 m; L_stall= 90 m)

На рис. 3 представлена основная расчетная схема решаемой задачи, а на рис. 4 представлены результаты моделирования НДС с различными λ_т от 0,3 до 1,6.

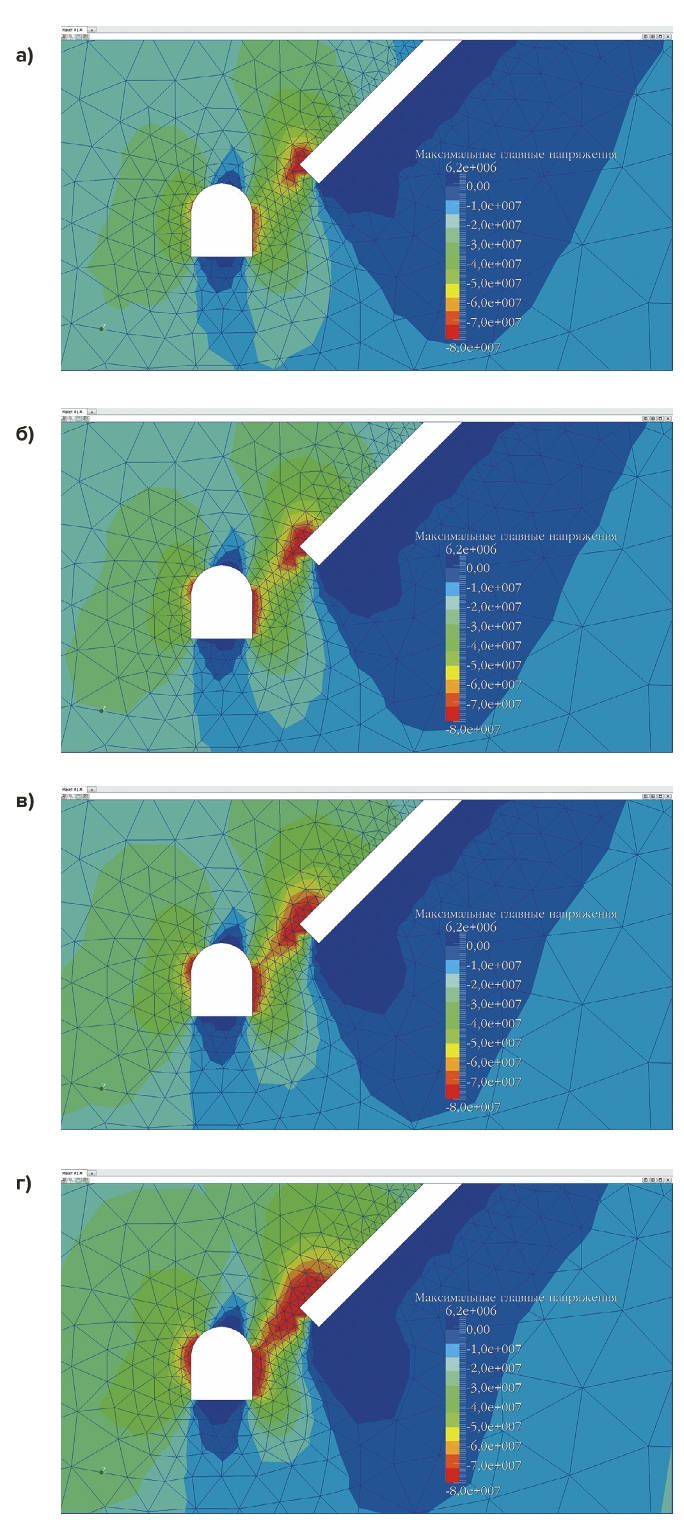Рис. 4 Результаты моделирования НДС массива горных пород, горных выработок и надштрекового целика при различных коэффициентах бокового отпора: а – 0,3 (по проф. А.Н. Диннику), б – 0,6 (по рекомендациям PRESS 3D URAL), в – 1,0 (гидростатическое), г – 1,6 (по данным: Руководство по геодинамическому районированию шахтных полей. СПб., 2012)

Fig. 4 Results of modelling the stress-and-strain state of the rock mass, mine drifts and the drift pillar at various lateral reaction pressure coefficients: а – 0.3 (by Prof. A.N. Dinnik), б – 0.6 (following recommendations in PRESS 3D URAL), в – 1.0 (hydrostatic), г – 1.6 (based on data from Guidance on geodynamic zoning of mine fields. St. Petersburg, 2012. (In Russ.))

Моделировалась отработка очистной камеры на глубине 500–550 м с углом падения 45 град и выемочной мощностью 2 м. Результаты расчета представлены в табл. 1. Максимальные сжимающие напряжения оценивались по ядру надштрекового целика.

Таблица 1 Результаты расчета НДС массива с различными λ_т
Table 1 Results of calculating the stress-and-strain state of the rock mass with various values of λ_т

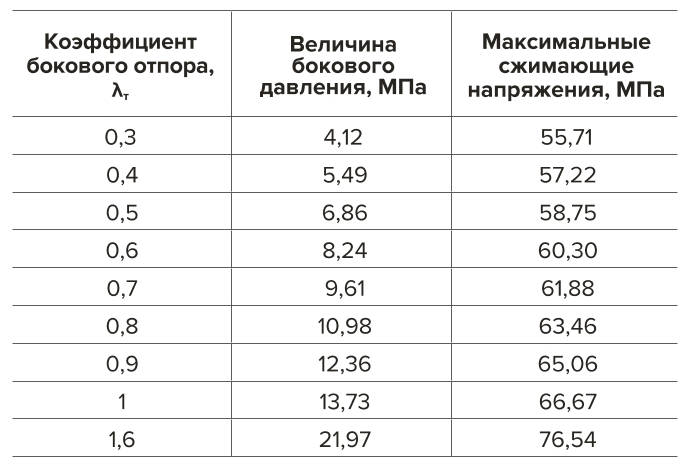
Стоит отметить, что при большем угле падения рудных тел – разница величин максимальных сжимающих напряжений будет больше, при меньшем угле падения – соответственно меньше, так как влияние вертикальной и горизонтальной составляющих напряжения значительно зависит от геометрии исследуемых рудных тел, жил, пластов и пр.

Оценка удароопасности рудного целика

Согласно п. 902 Правил безопасности склонными к горным ударам являются месторождения или их части, в пределах которых имеются горные породы и руды с высокими упругими свойствами, способные к хрупкому разрушению под нагрузкой. Такие месторождения относятся к склонным по горным ударам при достижении глубин, на которых действующие напряжения превышают 80% от предела прочности на сжатие горных пород месторождения.

В этой связи использование завышенного значения коэффициента бокового отпора приводит к ситуации, когда месторождение либо целиком ошибочно относится к склонным по горным ударам, либо критическая глубина удароопасности месторождения располагается значительно выше действительно напряженных глубин.

Таблица 2 Результаты оценки склонности массива к горным ударам

Table 2 Results of assessing the rock mass susceptibility to rock bumps

На примере хрупкого рудопородного массива с пределом прочности на одноосное сжатие, равном 90 МПа, в табл. 2 приведен результат оценки склонности массива к горным ударам. Значения максимальных сжимающих напряжений взяты из табл. 1.

Таким образом, демонстрируется ситуация, которая может привести к сложностям для нормальной работы горнодобывающего предприятия. Сложности будут связаны с учреждением комиссий по горным ударам, проведением дополнительных натурных измерений, увеличением параметров целиков и, как следствие, увеличением потерь в них [14].

Заключение

На основании выполненного комплекса оценки напряженного состояния массива горных пород предлагается новое решение актуальной научной задачи по прогнозированию естественного и техногенного геомеханического состояния массива горных пород.

На примере расчёта НДС целика демонстрируется необходимость корректного определения горизонтальной составляющей исходного поля напряжений. Завышенные значения коэффициента бокового отпора будут способствовать завышенным фактическим значениям коэффициента запаса при расчете параметров целиков, что, свою очередь, критично при разработке золоторудных месторождений. Заниженные значения коэффициента бокового отпора могут допустить непредсказуемое проявление горного давления в динамической форме.

Результаты, изложенные в статье, отражают опыт института ВНИМИ в области геомеханического обоснования конструктивных элементов систем разработки, параметров крепления горных выработок, размеров надштрековых целиков, а также при оценке склонности месторождений к горным ударам.

1 Правила безопасности при ведении горных работ и переработке твердых полезных ископаемых: федеральные нормы и правила в области промышленной безопасности, утв. приказом № 505 Федеральной службы по экологическому, технологическому и атомному надзору 08.12.2020 г. Режим доступа: http://www.gosnadzor.ru/industrial/mining/acts/general/ (дата обращения: 8 декабря 2020 г.)

Список литературы

1. Ливинский И.С., Митрофанов А.Ф., Макаров А.Б. Комплексное геомеханическое моделирование: структура, геология, разумная достаточность. Горный журнал. 2017;(8):51–55. https://doi.org/10.17580/gzh.2017.08.09

2. Рассказов И.Ю., Курсакин Г.А., Потапчук М.И., Мирошников В.И., Фрейдин А.М., Осадчий С.П. Геомеханическая оценка условий разработки глубоких горизонтов полиметаллического месторождения «Южное». Физико-технические проблемы разработки полезных ископаемых. 2012;(5):125–134.

3. Сосновская Е.Л., Авдеев А.Н. Прогноз потенциальной удароопасности нижних горизонтов Холбинского рудника. Известия вузов. Горный журнал. 2019;(8):30–37. https://doi.org/10.21440/0536-1028-2019-8-30-37

4. Еременко А.А., Гахова Л.Н., Еременко В.А. Влияние порядка отработки рудных залежей и технологических блоков на напряженно-деформированное состояние вмещающего массива в условиях полиметаллического месторождения. Горный информационно-аналитический бюллетень. 2015;(8):5–16. Режим доступа: https://giab-online.ru/files/Data/2015/08/5-16_8_2015.pdf?ysclid=l4n8zvis7365641289

5. Małkowski P., Niedbalski Z. A comprehensive geomechanical method for the as-sessment of rockburst hazards in underground mining. International Journal of Mining Science and Technology. 2020;30(3):345–355. https://doi.org/10.1016/j.ijmst.2020.04.009

6. Сидоров Д.В., Пономаренко Т.В. Методология оценки геодинамического состояния природно-техногенных систем при реализации проектов освоения месторождений. Горный журнал. 2020;(1):49–52. https://doi.org/10.17580/gzh.2020.01.09

7. Вершинин А.В., Левин В.А., Морозов Е.М. Прочностной анализ: Фидесис в руках инженера. М.: ЛЕНАНД; 2015. 408 с.

8. Соннов М.А., Котиков Д.А., Куранов А.Л. Применение CAE Fidesys в решении геомеханических задач. Горная промышленность. 2018;(5):90–92. https://doi.org/10.30686/1609-9192-2018-5-141-90-92

9. Мороз Н.Е., Белова М.В., Рукавишников Г.Д. Прогнозирование напряженных зон на различных этапах отработки золоторудного месторождения. Известия вузов. Горный журнал. 2021;(8):72–81. https://doi.org/10.21440/0536-1028-2021-8-72-81

10. Струков К.И., Рыльникова М.В. Проблемы и перспективы развития «Южуралзолото Группа компаний» в условиях проявления глобальных вызовов. Горная промышленность. 2021;(1):54–60. https://doi.org/10.30686/1609-9192-2021-1-54-60

11. Zhou Q., Liu D., Lin X. Pre-evaluation of fault stability for underground mining based on geomechanical fault-slip analysis. Geomatics, Natural Hazards and Risk. 2022;13(1):400–413. https://doi.org/10.1080/19475705.2022.2032401

12. Bewick R.P., Kaiser P.K., Amann F., Strength of massive to moderately jointed hard rock masses. Journal of Rock Mechanics and Geotechnical Engineering. 2019;11(3):562–575. https://doi.org/10.1016/j.jrmge.2018.10.003

13. Xu Wei, Jianping Zuo, Yue Shi, Haiyan Liu, Yunqian Jiang, Chang Liu, Experimental verification of parameter m in Hoek–Brown failure criterion considering the effects of natural fractures. Journal of Rock Mechanics and Geotechnical Engineering. 2020;12(5):1036–1045. https://doi.org/10.1016/j.jrmge.2020.01.006

14. Ponomarenko, T.; Nevskaya, M.; Jonek-Kowalska, I. Mineral Resource Depletion Assessment: Alternatives, Problems, Results. Sustainability 2021, 13, 862. https://doi.org/10.3390/su13020862