Геотехническое обоснование первоочередной разрезки залежей богатых руд шахты «Глубокая» методами пошагового численного моделирования в условиях гравитационно-тектонического поля напряжений

А.А. Давыдов¹, М.А. Соннов², А.Е. Румянцев³, Ю.Ю. Головченко³, А.В. Трофимов^3
1 ЗФ ПАО «ГМК «Норильский никель», г. Москва, Российская Федерация
² ООО «Фидесис», г. Москва, Российская Федерация
³ ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация
Горная Промышленность №5 / 2022 стр. 83-91

Резюме: В связи с разработкой месторождений на больших глубинах особую актуальность приобретают проблемы обеспечения устойчивости камер, выбор их ориентации и подбор крепи ещё на стадии проектирования объекта. На больших глубинах вблизи крупных тектонических нарушений фактор природного горного давления начинает играть определяющую роль в устойчивости подземных сооружений, а постоянный рост требований к повышению безопасности подземных сооружений предопределяет необходимость применения современных подходов по определению напряженно-деформированного состояния с применением численного моделирования. Принятие проектных решений без проведения моделирования может приводить к снижению экономической эффективности и безопасности производства, а иногда невозможности полноценного извлечения запасов. В исследовании конечно-элементное моделирование было использовано как один из основных методов определения оптимального варианта разрезки и отработки рудного тела богатых руд, расположенного в непосредственной близости от крупномасштабного тектонического нарушения, что провоцирует сложное напряженное состояние самого рудного тела. На практике метод конечных элементов может быть дискредитирован, а потому требуется описание последовательности методики построения и калибровки конечно-элементных моделей разрезок (вариантов отработки) для верного определения наиболее подходящего варианта отработки, что и сделано в настоящей работе. Комплексный подход включает в себя: формирование сложной пространственной геометрической модели рудных тел с учётом морфологических особенностей залегания; разделение модели на этапы отработки и формирование разных вариантов отработки; определение граничных условий для верного задания тензора Коши; определение модели деформирования и присвоение физико-механических параметров; проведение верификационных расчётов; расчёт всех вариантов моделей, их анализ и выбор наиболее оптимального способа отработки рудной залежи; интерполяцию данных в геомеханическую блочную модель для возможности выбора и обоснования параметров крепей и расчёта устойчивости камер по аналитическим методикам.

Ключевые слова: горные породы, литология, тектоника, целики, опорное давление, богатые руды, вкрапленные руды, закладочный массив, запас прочности, тензор

Для цитирования: Давыдов А.А., Соннов М.А., Румянцев А.Е., Головченко Ю.Ю., Трофимов А.В. Геотехническое обоснование первоочередной разрезки залежей богатых руд шахты «Глубокая» методами пошагового численного моделирования в условиях гравитационно-тектонического поля напряжений. Горная промышленность. 2022;(5):83–91. https://doi.org/10.30686/1609-9192-2022-5-83-91

Информация о статье

Поступила в редакцию: 11.09.2022

Поступила после рецензирования: 28.09.2022

Принята к публикации: 29.09.2022

Информация об авторах

Давыдов Андрей Александрович – руководитель проектного офиса комплексного развития рудника «Скалистый», ЗФ ПАО «ГМК «Норильский никель», г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Соннов Максим Александрович – действительный член Академии горных наук, заместитель генерального директора по продажам, ООО «Фидесис», г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Румянцев Александр Евгеньевич – кандидат технических наук, главный специалист лаборатории геотехники, ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация; ORCID: 0000-0002-2204-961X; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Головченко Юрий Юрьевич – младший научный сотрудник лаборатории геотехники, ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация; ORCID: 0000-00032980-2173; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Трофимов Андрей Викторович – действительный член Академии горных наук, кандидат технических наук, заведующий лабораторией геотехники, ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация; ORCID: 0000-0001-7557-9801; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

При разработке полезных ископаемых на большой глубине особое внимание следует уделять проблеме устойчивости камер, выбору их ориентации и подбору крепи еще на стадии проектирования. Подобные работы заведомо сопряжены с достаточно большими рисками ввиду значительного горного давления. Однако при отработке залежей вблизи крупных тектонических нарушений данный фактор начинает играть решающую роль [1; 2]. Сложное напряженно-деформированное состояние (НДС) массива в подобных зонах должно быть обязательно учтено при проектировании подземных сооружений и ведении очистных работ. Использование моделирования методом конечных элементов помогает получить НДС массива с учетом тектонических нарушений, литологии и даже предварительно заданного природного поля напряжений.

Численное моделирование само по себе не является чем-то новым в сфере решения подобных задач, однако его постоянное развитие помогает учитывать различные особенности поведения скальных массивов, что нашло отражение в работе [3], где приведена разработка новой упруго-пластической модели материала, или же в статье [4], где приводится методология численного моделирования с учетом напряжений, которые возникают в процессе очистных работ.

Ввиду своей универсальности метод конечных элементов в численном моделировании используется сегодня для решения разнообразных задач. Так, в работе [5] рассматривается методика определения НДС трещиноватого массива методом конечных элементов. В статье [6] приводится методика прогноза физико-механических характеристик блочного скального массива при помощи численного моделирования. В исследовании [7] приведена нетривиальная методика оценки сжимаемости порового объёма пористых горных пород, для чего была использована конечно-элементная модель на основе данных компьютерной томографии.

Использование численного моделирования дает возможность получить представление о различных процессах, протекающих в скальных массивах, и выяснить взаимосвязь между ними, что нашло отражение в работе [8]. При разработке численных конечно-элементных моделей особое внимание следует уделять построению сеток [9], поскольку от качества и количества конечных элементов напрямую зависит точность результатов проводимого моделирования. Использование адаптивных сеток позволяет решить проблему перегруженности модели и сохранить точность получаемого решения для интересующих областей [10].

Однако, стоит отметить, что численные методы – это в первую очередь инструмент, использование которого сопряжено с рядом допущений и проблем, что всегда должно учитываться при анализе полученных результатов и моделировании в целом [11]. При расчете скальных массивов это особенно актуально ввиду большой сложности моделируемых структур и широкого спектра моделируемых задач [12].

Моделирование

Для отработки части месторождения, залегающего в непосредственной близости к крупномасштабному тектоническому нарушению, необходимо выполнить предварительное геомеханическое обоснование вариантов разрезки и отработки руд месторождения с применением конечно-элементного моделирования.

Численная модель разработана в программном обеспечении CAE Fidesys с целью оценки напряженно-деформированного состояния массива Октябрьского месторождения в поле шахты «Глубокая» рудника «Скалистый».

Для корректного моделирования напряженно-деформируемого состояния массива необходимо воссоздать историю его нагружения. Иными словами, массив перед началом отработки находится в преднапряженном состоянии, которое вызвано по большей мере действием горного давления от веса породной толщи и тектоническими нарушениями. Для получения корректного распределения напряжений принципиально важными являются следующие аспекты:

1. Задание в геометрии модели сложного пространственного залегания;
2. Учет сложной геометрии интрузии;
3. Введение в модель тектонических нарушений, являющихся зонами ослаблений, по которым происходит смещение блоков пород друг относительно друга.

На первом этапе для формирования объёмной твердотельной модели залежей богатых руд шахты «Глубокая» рудника «Скалистый» литологические разности в виде каркасов импортированы из блочной геомеханической модели, созданной в программе ГГИС Micromine. Ввиду особых требований программ конечно-элементного моделирования к качеству триангуляции и по причине того, что при импорте из ГГИС систем частыми являются различные артефакты геометрии в виде разрывов полигональной сети, взаимного наложения поверхностей или их пересечения, для создания сложной морфологии геологических структур на основе импортированных каркасов проводилась их регуляризация и упрощение топологии, а для определения пересечения поверхностей создан авторский скрипт, написанный на языке программирования Python с использованием библиотек ezdxf, pandas, scipy.

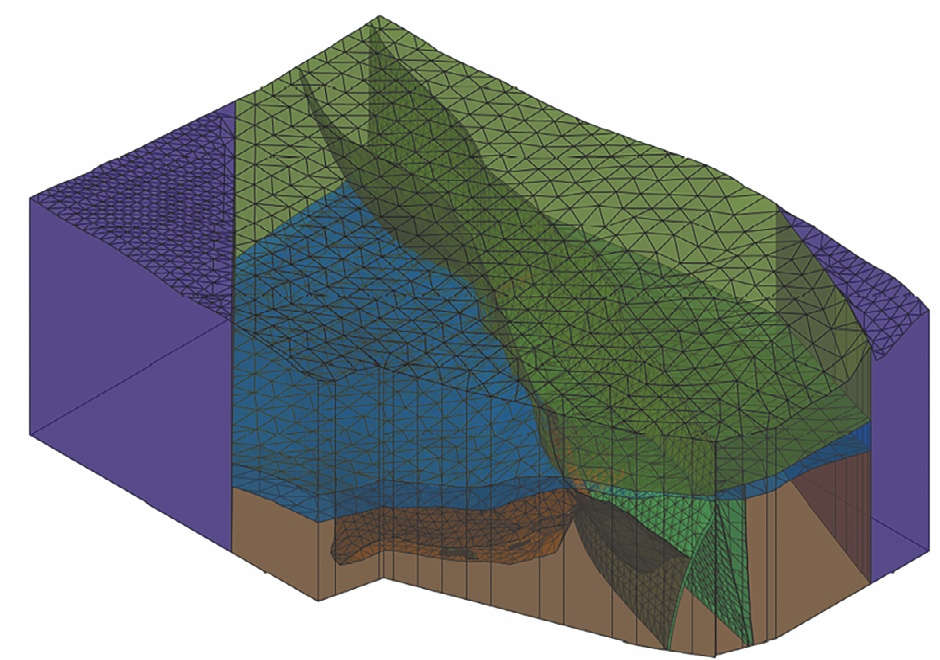Рис. 1 Общий вид модели каркасов в программе AutoCad после обработки каркасов

Fig. 1 General view of an AutoCad wireframe model after processing the wireframes

После перестроения геометрии рудные тела имеют равномерную триангуляцию (рис. 1), при этом полностью повторяют морфологию первоначальных каркасов и имеют значительно меньшее количество треугольников. Моделирование геометрии производилось с рядом допущений. В частности:

1) из опыта эксплуатации моделируемый массив должен иметь минимальную толщину в 5 м;

2) тела, находящиеся достаточно близко (менее метра) друг к другу, объединены в единые;

3) тектоническим нарушениям, заданным в виде плоскости, придавалась мощность 10 м.

На втором этапе геотехниками совместно с технологами сформированы 5 различных вариантов отработки рассматриваемых рудных тел, представлены на рис. 2.

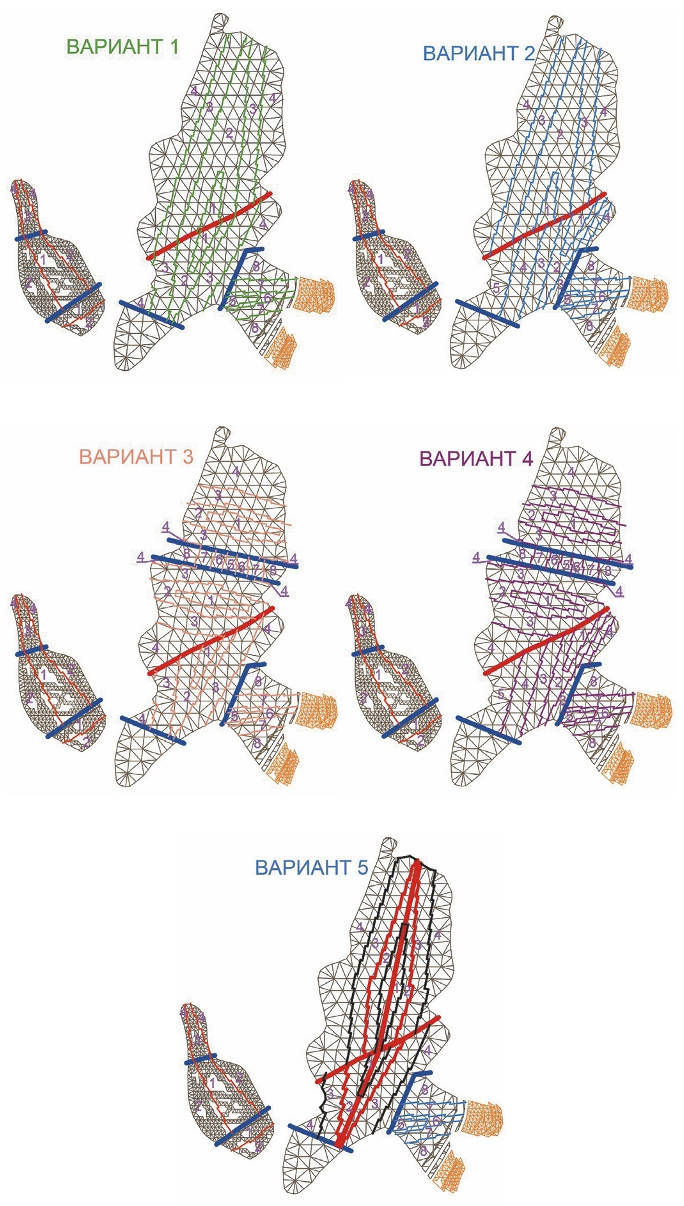Рис. 2 Варианты отработки при различной ориентации очистных камер: вариант 1 и 2 – субмеридиональная разрезка от тектонического нарушения с субширотным направлением движения фронтов, отличаются друг от друга только южной частью в залежи С-6; вариант 3 и 4 – субширотная разрезка с оставлением разделительного массива с субмеридиональным направлением движения фронтов, отличаются друг от друга только южной частью в залежи С-6; вариант 5 – субмеридиональная разрезка от центра запасов

Fig. 2 Mining options with different stope orientations: Options 1 and 2: submeridional splitting from a tectonic disturbance with sublatitudinal front advancement; the two options are only different in the southern part in the C-6 deposit; Options 3 and 4: sublatitudinal splitting while keeping a separating rock mass with submeridional front advancement; the two options are only different in the southern part in the C-6 deposit; Option 5: submeridional splitting from the centre of the deposits

На третьем этапе в программе Autocad производилась разрезка модели в соответствии с вариантами отработки. Пример разрезки богатых руд представлен на рис. 3.

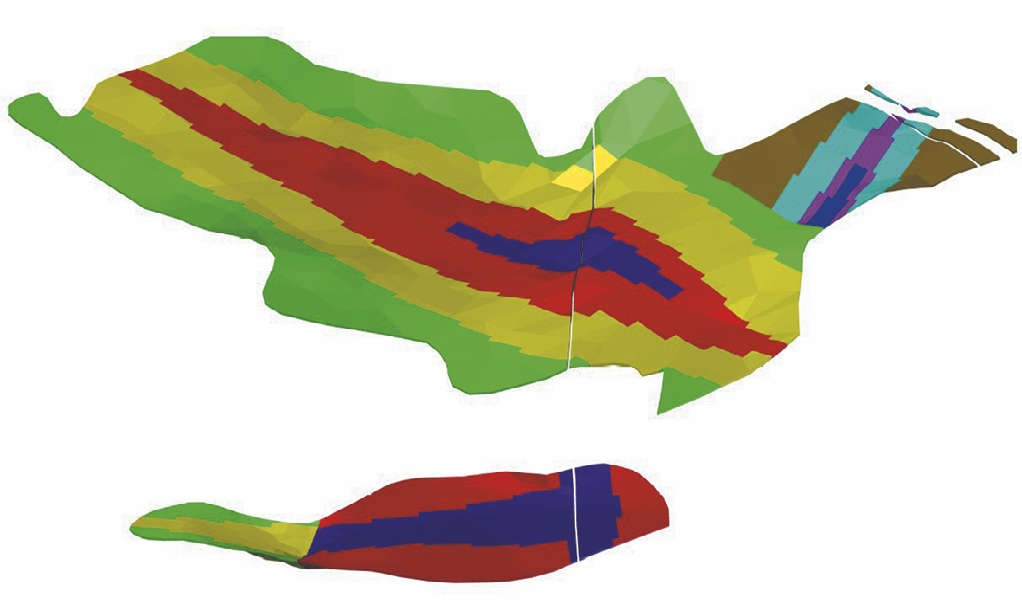Рис. 3 Разрезка рудного тела богатых руд (вариант 1)

Fig. 3 Splitting of a rich ore body (Option 1)

В дальнейшем полученные тела были последовательно импортированы в CAE Fidesys и разнесены по отдельным группам. Далее были импортированы тектонические нарушения. После импорта всех необходимых тел были произведены булевы операции вычитания.

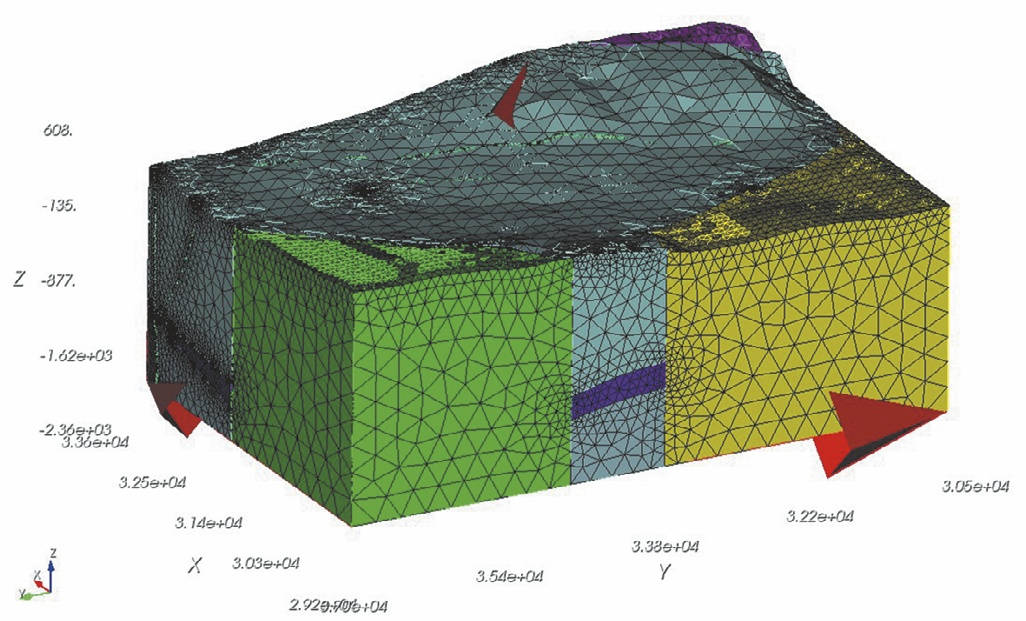Рис. 4 Общее представление моделей

Fig. 4 General representation of the models

Модель строилась до земной поверхности с повторением рельефа. Для исключения влияния краевых эффектов и выполнения принципа Сен-Венана рудные тела помещались в объём большого размера (рис. 4), размер объёма с юга на север (ось Y) – 6200 м, с запада на восток (ось X) – 4000 м, по абсолютному значению глубины (ось Z) – 2500 м. Модель строилась в координатах блочной модели с целью возможности дальнейшего экспорта результатов моделирования в блочную геомеханическую модель.

На четвёртом этапе задавалась логика пошагового расчёта с присвоением физико-механических свойств всем литологическим разностям.

Физико-механические параметры для численной модели приняты на основе распределения показателей в блочной геомеханической модели Октябрьского месторождения в поле рудника «Скалистый» и представлены в табл. 1.

Таблица 1 Физико-механические параметры, принятые для расчёта модели
Table 1 Physical and mechanical parameters adopted for the model calculations

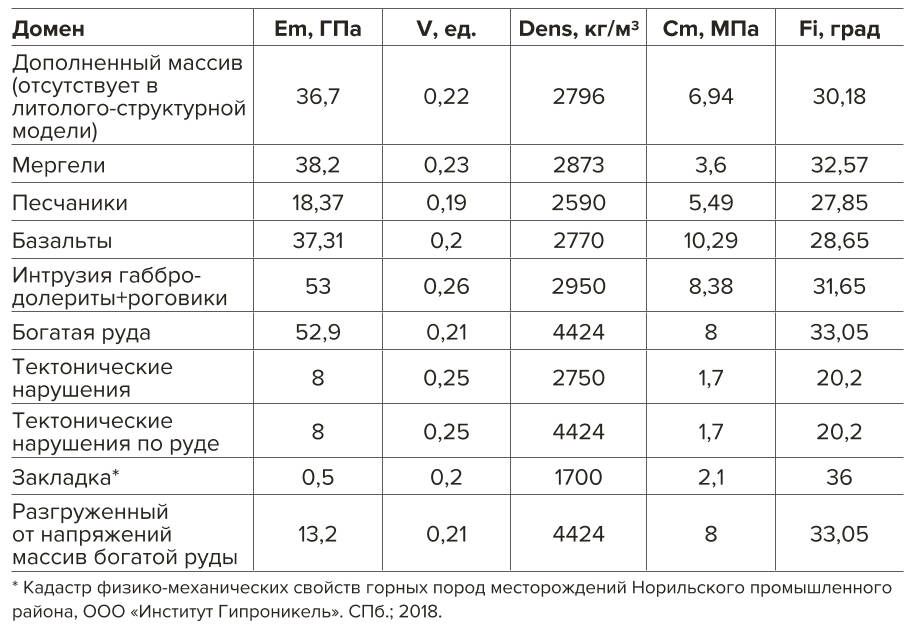
Следует отметить, что применена идеально-упругопластическая модель грунта с критерием Друкера-Прагера с пересчётом на промежуточный конус относительно пирамиды Кулона-Мора (среднее между вписанным и описанным конусом).

Промежуточный конус Друкера-Прагера:

, (1)

где A_п и B_п – параметры Друкера-Прагера (для промежуточного конуса).

Моделирование подразумевает последовательное ведение отработки путём замены физико-механических свойств в блоках с обнулением полученных на предыдущих шагах расчёта напряжений путём присвоения нулевого тензора физико-механическим характеристикам закладочного массива. Пример задания физико-механическим характеристикам нулевого тензора приведён на рис. 5.

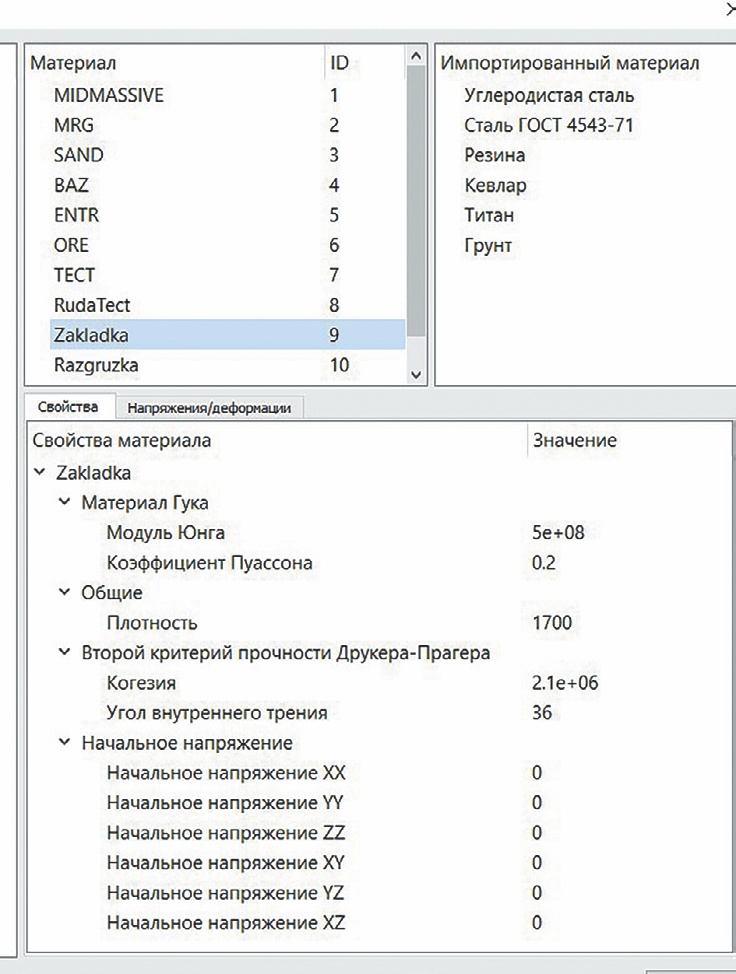Рис. 5 Задание начального нулевого тензора закладочному массиву

Fig. 5 Setting the initial zero tensor to the backfill mass

Пошаговое моделирование осуществляется за 10 шагов:

1. Шаг 1: моделируется исходное состояние массива до отработки (природное напряжённо-деформированное состояние);

2. Шаг 2: моделируется разгрузка массива от повышенных напряжений;

3. Шаг 3: моделируются выемка и закладка богатых руд, и разгрузка массива, подлежащего отработке, от повышенных напряжений;

4. Шаги 4–10: осуществляются последовательная отработка, закладка и разгрузка массива богатых руд в соответствии с вариантами разрезок (всего 5 вариантов, см. рис. 2).

На пятом этапе для моделирования напряженно-деформированного состояния массива заданы граничные условия, которые включали в себя:

‒ исключение перемещений: по вертикальной оси Z для нижней плоскости модели и для двух боковых граней по нормалям к поверхностям (рис. 6);

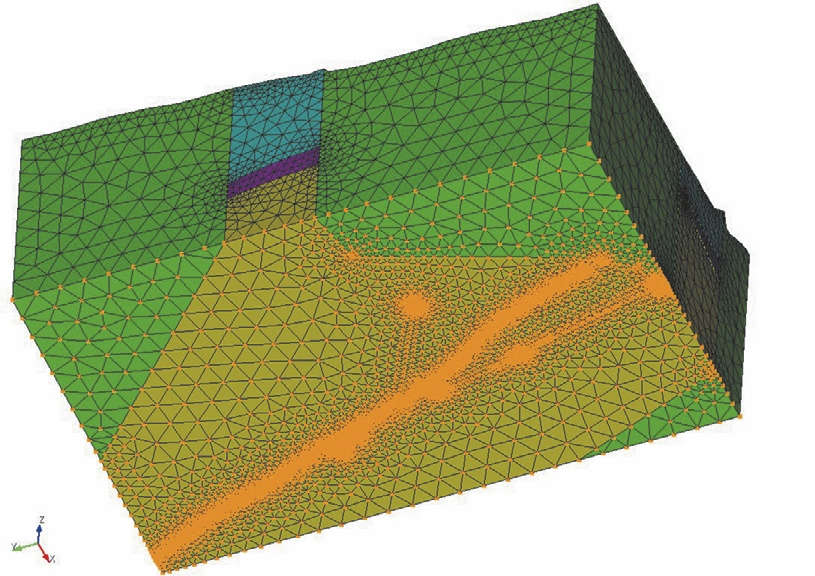
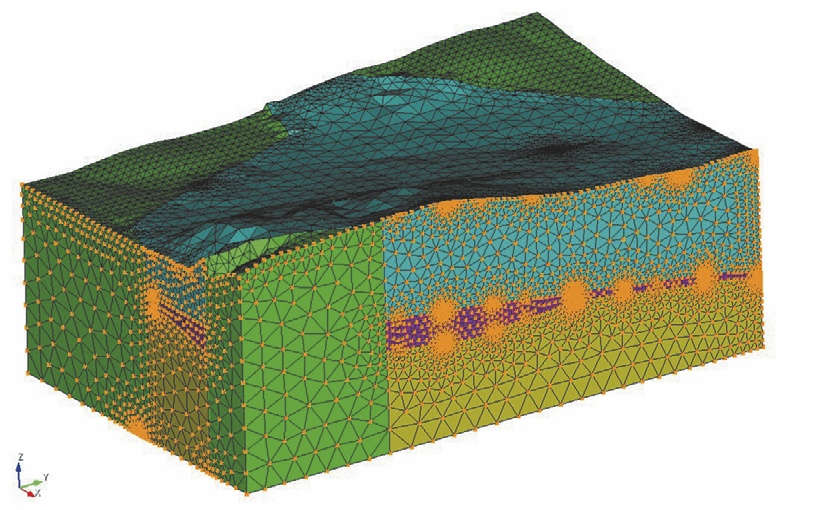Рис. 6 Исключение перемещений: по оси Z для нижней грани модели и для двух боковых граней в модели

Fig. 6 Displacement exclusion: along the Z-axis for the lower boundary of the model and for the two lateral boundaries in the model

‒ оценка природного тензора напряжений по дискованию керна, пример представлен на рис. 7;

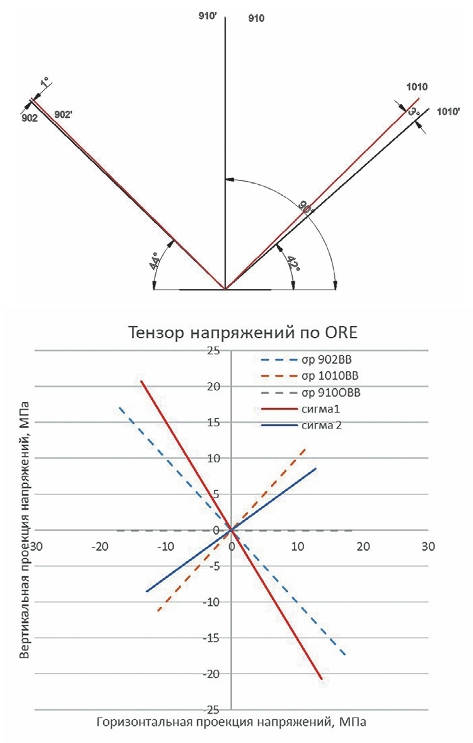Рис. 7 Распределение напряжений относительно радиальных напряжений, вызывающих дискование керна

Fig. 7 Stress distribution in relation to radial stresses that cause the rock core slicing

‒ поворот тензора напряжений в координаты модели;

‒ нагрузками в модели является собственный вес пород до поверхности, который реализован через присвоение гравитации всем узлам модели и задание компонент тензора напряжений для оставшихся двух боковых граней, а именно XX, YY, XY (рис. 8), соответствующих направлениям X и Y.

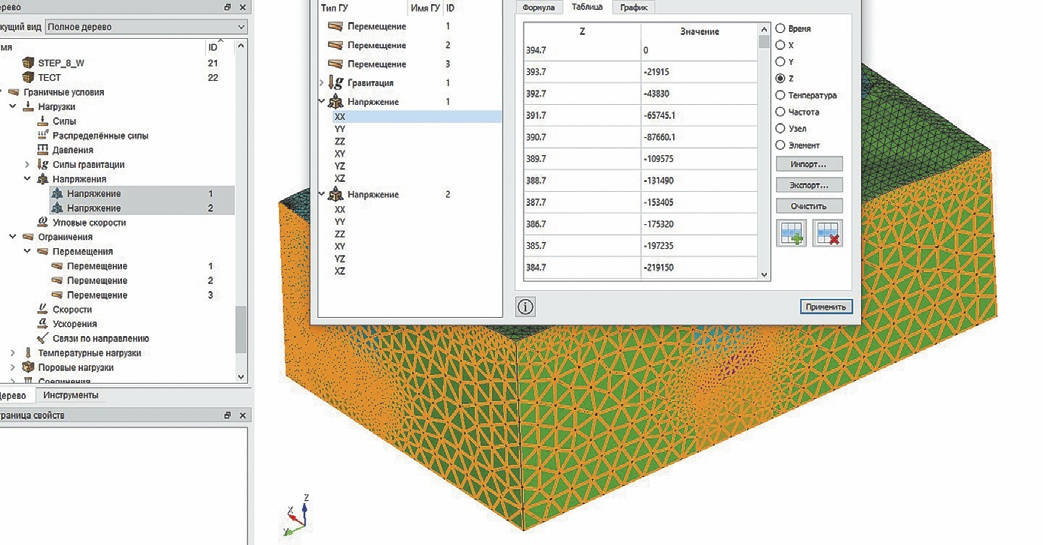Рис. 8 Задание напряжений на боковые грани модели по оставшимся плоскостям X и Y

Fig. 8 Stress assignment to the lateral faces of the model in the remaining X and Y planes

Поворот природного тензора напряжений в координаты моделей

Ориентация природного тензора напряжений в модели представлена на рис. 9. Необходимо повернуть тензор в плоскости модели для задания напряжений на границы модели.

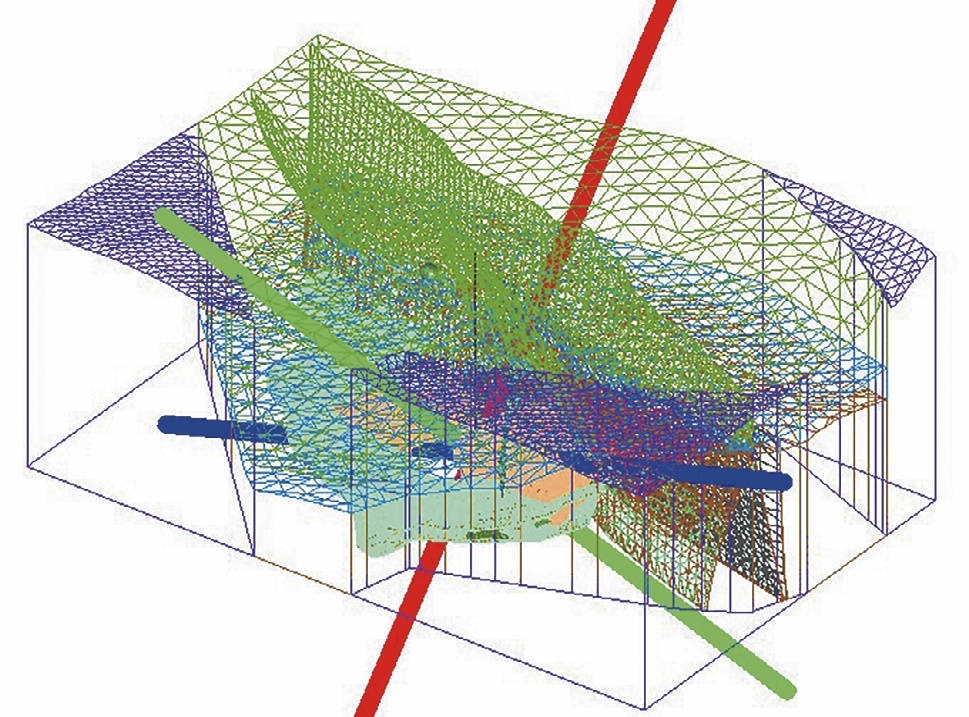Рис. 9 Ориентация тензора главных напряжений в модели

Fig. 9 Orientation of the principal stress tensor in the model

На рис. 9 красным цветом указаны главные максимальные напряжения, зелёным –промежуточные главные напряжения, синим – минимальные главные напряжения. По результатам дискования керна установлено, что максимальные главные напряжения по значениям соответствуют давлению от высоты столба горных пород, поэтому поворот тензора происходит следующим образом:

σ₃ – максимальное напряжение означает вертикальное напряжение в массиве;

σ₂ – минимальное горизонтальное напряжение равно 0,45 · σ₃ (по результатам дискования керна);

σ₁ – максимальное горизонтальное напряжение равно 0,7 · σ₃ (по результатам дискования керна).

Вычислим тензор для заданных начальных условий:

– глубина h = 2144 м;

– приведенная плотность (вес) породы γ = 2744,3 кг/м³ (определялась как среднее для базальтов, песчаников и мергелей).

Тогда:

σ₃ = –g · γ · h = –9,81 · 2744,3 · 2144 = –57719874 Па;

σ₂ = 0,45 · σ₁ = 0,45 · (–57719874) = –25973943 Па;

σ₁ = 0,68 · σ₁ = 0,7 · (–57719874) = –40403912 Па.

Запишем полученный тензор:

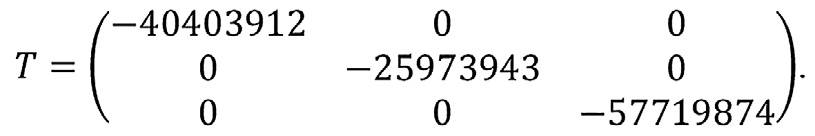
Получим углы из тензора в AutoCAD. Общий вид тензора и необходимых осей показан на рис. 10.

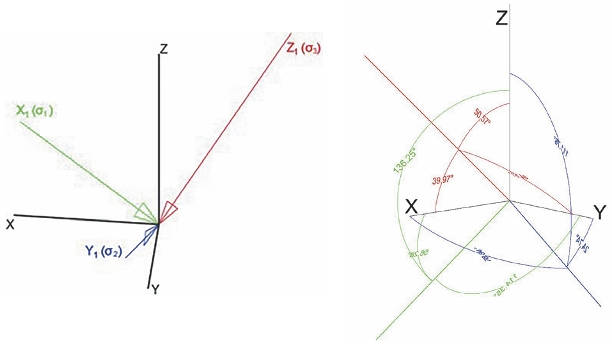Рис. 10 Тензор напряжений

Fig. 10 Stress tensor

Поворот тензора выполняется в соответствии со следующей формулой:

T₁ = C · T · C^T.

Запишем матрицу C для данной задачи:

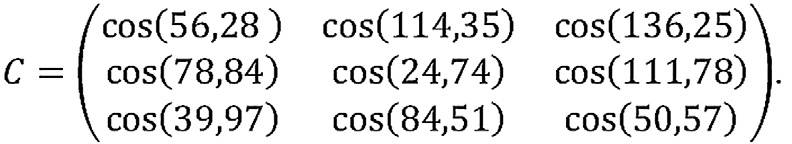
Тогда тензор T1 будет равен:

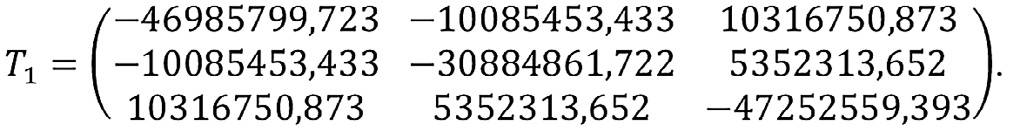
На шестом шаге после предварительного расчёта происходит верификация модели путём сравнения напряжений в модели и ориентации тензора напряжений.

Верификация природного поля напряжений в рудном теле и направление векторов представлены на рис. 11 (красным, зелёным и синим цветами, что соответствует максимальному, промежуточному и минимальному векторам напряжений).

Рис. 11 Природное поле напряжений в виде векторов главных напряжений

Fig. 11 Natural stress field represented by principal stress vectors

На седьмом шаге осуществлён расчёт всех моделей, проведён их анализ и выбран наиболее безопасный с точки зрения геомеханических рисков.

В качестве критерия обеспечения прочности массива принят критерий удароопасности¹: σ_1(max) ≥ 0,7 · σ_сж. При таком уровне напряжённости необходим инструментальный контроль удароопасности.

Запас прочности оценивался по критерию Кулона–Мора по следующей зависимости:

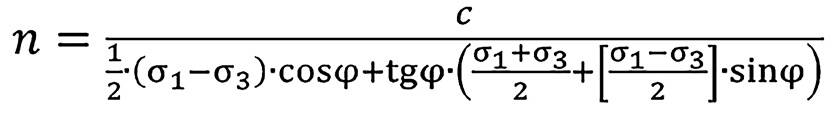, (2)

где c – сцепление, МПа; σ₁ и σ₃ – первое и третье главные напряжения, МПа; φ – угол внутреннего трения, град. При n < 1 фиксируется неустойчивое состояние.

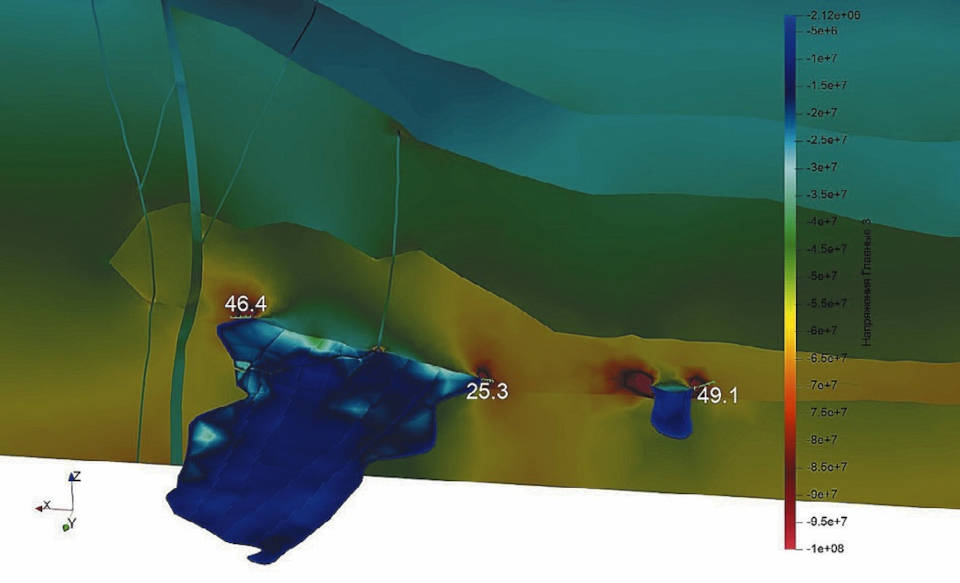Рис. 12 Расстояния, на которых рекомендуется строить оконтуривающие выработки

Fig. 12 Recommended distances to drive the contour drifts

На рис. 12 представлены расстояния, на которых рекомендуется строить оконтуривающие выработки, чтобы минимизировать влияние горного давления на них. При этом минимальное расстояние не должно быть ближе 26 м к контурам рудных тел, так как на указанном расстоянии максимальные главные напряжения находятся на границе величин, которые способны приводить к разрушению выработок. Рекомендуемое расстояние размещения оконтуривающих выработок 50 м, так как на указанном расстоянии напряжения снижаются до безопасных величин, но, необходимо отметить, что величины напряжений не достигают природных и превышают их на 15–30%.

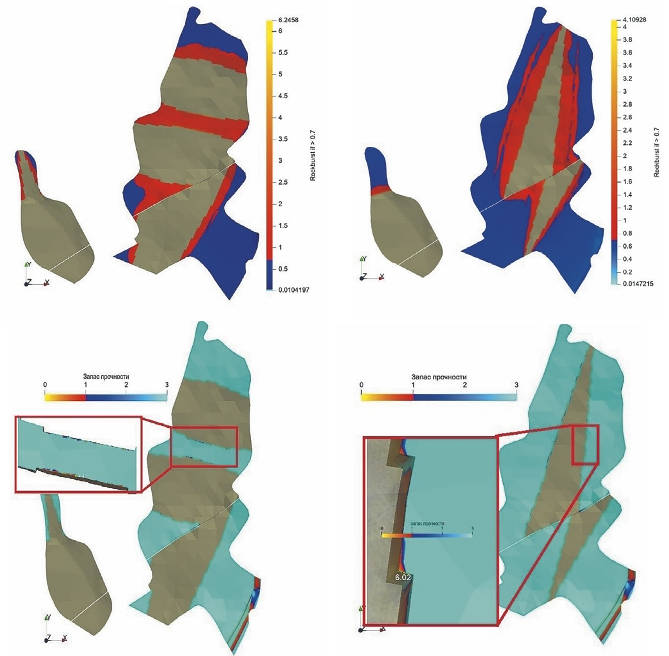Рис. 13 Анализ одного из шагов расчёта модели с субмеридиональной разрезкой и субширотной разрезкой

Fig. 13 Analysis of one of the calculation steps for the models with submeridional splitting and with sublatitudinal splitting

Пример анализа одного из шагов расчёта модели с субмеридиональной разрезкой и субширотной разрезкой представлен на рис. 13. Как видно, при субширотной разрезке формируется целик, напряжения в котором превышают 0,7σсж, т.е. целик находится в удароопасном состоянии, отработка такого массива будет весьма затруднительна, субмеридиональная разрезка на этом фоне выглядит значительно предпочтительнее ввиду отсутствия необходимости формировать разделительные массивы для поддержания интенсивности отработки руды. Ввиду большой глубины ведения работ и высоких компонент напряжений разгрузочные мероприятия необходимо проводить во всех вариантах разрезок. Негативное влияние компонент горизонтальных напряжений для субмеридиональных разрезок не так велико из-за компенсации деформаций тектоническими нарушениями.

На восьмом шаге значения полей напряжений в каждом расчётном узле экспортируются в csv файл для импорта значений в блочную геомеханическую модель в ГГИС Micromine, в которой осуществлён расчёт рейтинга Q-Бартона с учётом действующих напряжений. Результатом такой интерполяции является возможность подбора крепления с высокой точностью ещё на стадии проектирования выработок. На рис. 14 представлен пример процесса оценки напряжений и построения гистограмм в ГГСИ Micromine.

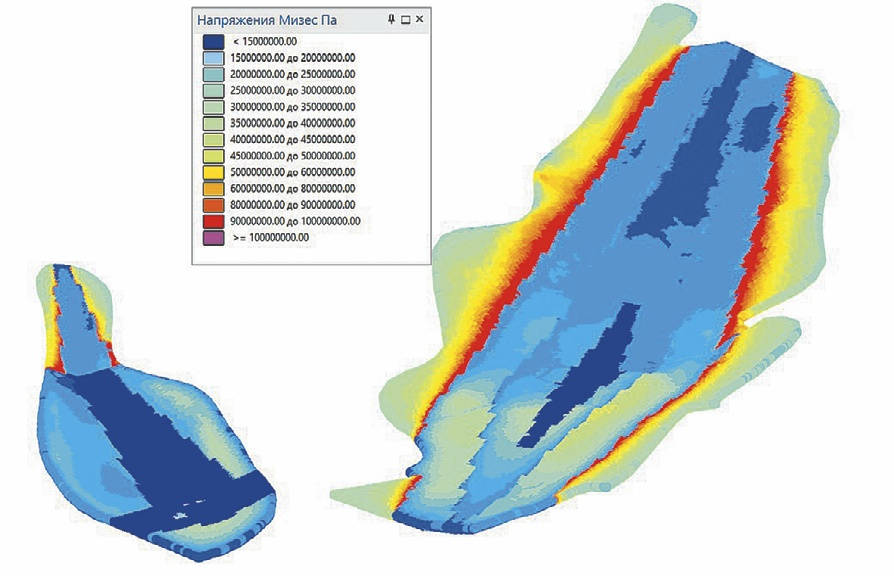
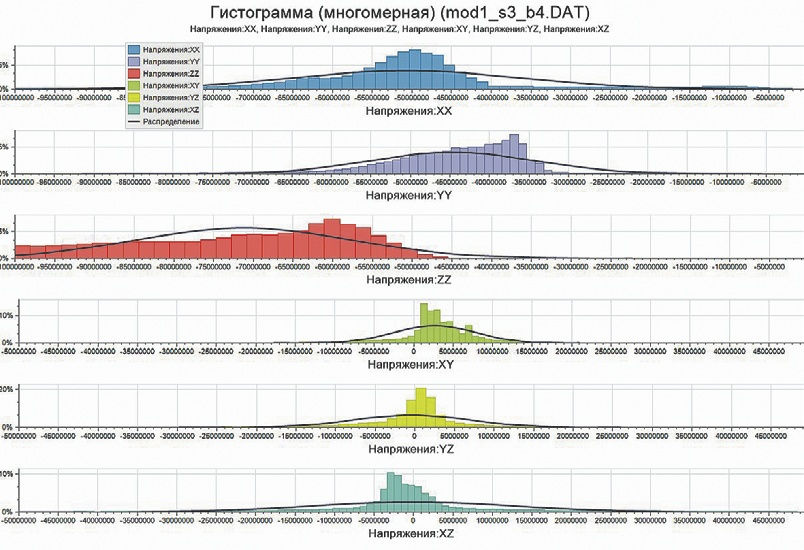Рис. 14 Пример процесса оценки напряжений и построения гистограмм в ГГСИ Micromine

Fig. 14 An example of the stress assessment process and bar chart plotting in the Micromine Mining Software

Заключение

1. В статье представлена методология формирования и расчёта глобальной численной модели в CAE Fidesys с использованием дополнительных инструментов в виде специальной авторской программы написанной на языке Python, программы ГГИС Micromine, CAD AutoCad;

2. До начала ведения работ максимальные главные напряжения достигают 56 МПа в центральной части залежи С-6 (как раз в области возможного целика). Минимальные главные напряжения сконцентрированы в зонах тектонических нарушений, приуроченных к НХР, и составляют 15 МПа. Это связано с тем, что физико-механические характеристики рудного массива, пересекаемого тектоникой, значительно ниже, чем у основной части рудного массива. Однако именно в тектонически нарушенных рудных зонах коэффициент запаса даже до начала ведения очистных работ ниже 1. До начала ведения работ массив не склонен к горным ударам;

3. Расстояния, на которых рекомендуется строить оконтуривающие выработки, чтобы минимизировать влияние горного давления на них: минимальное расстояние не должно быть ближе 26 м к контурам рудных тел, так как на указанном расстоянии максимальные главные напряжения находятся на границе величин, которые способны приводить к разрушению выработок. Рекомендуемое расстояние размещения оконтуривающих выработок – 50 м, так как на указанном расстоянии напряжения снижаются до безопасных величин, но, необходимо отметить, что величины напряжений не достигают природных и превышают их на 15–30%;

4. Наилучшим вариантом разрезки с точки зрения возникающих геомеханических рисков является вариант 1, поскольку являет собой равномерную отработку в северном и южном направлениях. При этом вариант 5 тоже может применяться, однако необходимо соблюдение непревышения опережения фронта работ в южной части залежи С-6, что обусловливает более позднее введение его в работу. Вариант субмеридиональной разрезки со смещенным южным фронтом менее предпочтительный. Следует отметить, что необходимо формировать равномерные фронты отработки с учётом потребности бизнеса в объёмах добычи руды;

5. Варианты с субширотной разрезкой равнозначны между собой. В них особое внимание следует уделить последовательности отработки, чтобы не формировались зоны опорного давления в виде клина. Формирующийся целик в северной части залежи С-6 в обоих вариантах идентичен и на данном этапе изученности массива не рекомендуется к применению с точки зрения геомеханических рисков;

6. По результатам моделирования установлено, что ориентация тензора напряжений не оказывает значительного влияния на устойчивость камер, что подтверждается коэффициентом запаса устойчивости, так как разрушению подвержены сугубо угловые части модели вне зависимости от ориентации камер. Однако при формировании целика в северной части залежи С-6 зоны с коэффициентом запаса ниже 1 формируются на всей его протяжённости вглубь до 4 м;

7. Разрезка юго-восточной части залежи С6 в субширотном направлении является верным решением, так как работы приближаются к тектоническим нарушениям, оперяющим НХР. Видно, что из-за перераспределения напряжений от заложенного пространства осложнения могут возникать в северной части рассматриваемой области, что и подтверждается увеличенной зоной, склонной к потенциальным горным ударам;

8. Следует отметить, что нельзя в полной мере по указанным моделям говорить об объёмах разрушений, поскольку модели глобальные и отражают лишь качественную картину поведения массива. Результаты, полученные при их расчёте, являются отправной точкой для формирования локальных моделей. Несмотря на предполагаемую ориентацию тензора напряжений, где максимальное горизонтальное напряжение направлено в субширотном направлении, вариант разрезки в субширотном направлении двумя фронтами с оставлением разделительного массива считать наиболее опасным по сравнению с разрезками в субмеридиональном направлении;

9. Если указать последовательность вариантов от наилучшего к наихудшему, то будет 1, 5(2), 3(4). Субмеридиональная разрезка наиболее предпочтительна;

10. Отработку необходимо начинать после приведения массива в неудароопасное состояние, а сами работы вести в защищённых зонах в соответствии с действующими нормативными документами. Отработку вблизи тектонических нарушений необходимо вести в соответствии с указаниями;

11. Использование единой системы координат при создании геомеханической блочной модели и пошаговой численной модели позволило оценить изменение напряженно-деформированного состояния при отработке всех запасов богатых руд с применением ГГИС Micromine, в которой осуществлён расчёт рейтинга Q-Бартона с учётом действующих напряжений. Результатом такой интерполяции является возможность подбора крепления с высокой точностью ещё на стадии проектирования выработок. А полученные компоненты тензора напряжений могут применяться в качестве граничных условий при решении локальных численных задач.

Список литературы

1. Соннов М.А., Румянцев А.Е., Трофимов А.В., Вильчинский В.Б. Геотехническое обоснование отработки залежей, ограниченных тектоническими нарушениями на основе применения конечно-элементного моделирования. Горная промышленность. 2018;(5):107–110. https://doi.org/10.30686/1609-9192-2018-5-141-107-110

2. Федотова Ю.В., Каспарьян Э.В., Кузнецов Н.Н. Влияние активных разломов на напряженное состояние неоднородных массивов скальных пород. В кн.: Адушкин В.В., Кочарян Г.Г. (ред.) Триггерные эффекты в геосистемах: материалы IV Всероссийской конференции с международным участием, г. Москва, 6–9 июня 2017 г. М.: ГЕОС; 2017. С. 318–326.

3. Zhou X.-P., Zhang T., Qian Q.-H. A two-dimensional ordinary state-based peridynamic model for plastic deformation based on DruckerPrager criteria with non-associated flow rule. International Journal of Rock Mechanics and Mining Sciences. 2021;146:104857. https://doi.org/10.1016/j.ijrmms.2021.104857

4. Wang Y., Huang J., Wang G. Numerical analysis for mining-induced stress and plastic evolution involving influencing factors: high in situ stress, excavation rate and multilayered heterogeneity. Engineering Computations. 2022;39(8):2928–2957. https://doi.org/10.1108/EC-10-2021-0614

5. Конурин А.И., Неверов С.А., Неверов А.А., Щукин С.А. К проблеме численного моделирования напряженно-деформированного состояния и устойчивости трещиноватого массива. Фундаментальные и прикладные вопросы горных наук. 2019;6(2):144–150. https://doi.org/10.15372/FPVGN2019060225

6. Вербило П.Э. Численное моделирование блочного горного массива при различных схемах нагрузки. Процессы в геосредах. 2015;4(4):5–11.

7. Moosavi S.A., Goshtasbi K., Kazemzadeh E. An evaluation method of rock pore volume compressibility determination using a computed tomography scanned-based finite element model. Acta Geophysica. 2022. https://doi.org/10.1007/s11600-022-00874-9

8. Feng F., Chen S., Zhao X., Li D., Wang X., Cui J. Effects of external dynamic disturbances and structural plane on rock fracturing around deep underground cavern. International Journal of Coal Science and Technology. 2022;9(1):15. https://doi.org/10.1007/s40789-022-00487-z

9. Нестеров И.В., Мерзлякова А.Д. Особенности формирования адаптивных сеток МКЭ для решения задач геотехники. В кн.: Власов А.Н., Карнет Ю.Н., Муковникова И.И. (ред.). Механика композиционных материалов и конструкций, сложных и гетерогенных сред: сборник трудов 11-й Всероссийской научной конференции с международным участием, г. Москва, 23–25 ноября 2021 г. М.; 2021. С. 356–361. https://doi.org/10.33113/conf.mkmk.ras.2021.356_361.42

10. Zhang Z., Mei G., Xu N. A geometrically and locally adaptive remeshing method for finite difference modeling of mining-induced surface subsidence. Journal of Rock Mechanics and Geotechnical Engineering. 2022;14(1):219–231. https://doi.org/10.1016/j.jrmge.2021.11.001

11. Сеттиев Ш.Р. Численный расчет: проблемы и методы их решения. Потенциал современной науки. 2016;(6):6–10.

12. Конурин А.И., Неверов С.А., Неверов А.А. Особенности построения параметрической модели геосреды для численного моделирования напряженного состояния массива пород. Интерэкспо Гео-Сибирь. 2018;6:89–99.