Обоснование применимости мозаичной системы целиков в безрудных блоках при отработке жильных месторождений золота

Д.Н. Ермошкин¹, К.З. Курманалиев², В.А. Мансуров³, В.И. Межеловский⁴, Е.А. Бабкин^3
1 Global Asia Management, г. Бишкек, Кыргызская Республика
² Геолэкспертпроект, г. Бишкек, Кыргызская Республика
³ Vertex Gold Co, г. Бишкек, Кыргызская Республика
⁴ Глобал Ширальджин Майнинг, г. Бишкек, Кыргызская Республика
Горная Промышленность №3 / 2023 стр. 108-114

Резюме: Рассмотрены вопросы формирования самоподобных, иерархически масштабированных, фрактальных свойств рудных и безрудных подсистем блоков в контуре оруденения. Безрудные инвариантные блоки предусматривается выделять для организации целиков в укрупненных контурах эксплуатационных блоков, размерностью до 160 м по простиранию и до 120 м по падению тонких жильных тел, для механизированной слоевой из подэтажных штреков системы очистных работ. Подсистемы рудных и безрудных блоков обладают сходной фрактальной размерностью и степенной иерархией, близкой к коэффициенту 2. Применение метода оставления в целиках безрудных интервалов за счет снижения затрат на буровзрывные работы и откатку объема целиков (до 14%) на горно-подготовительные и очистные работы в значительной мере сокращает удельные эксплуатационные затраты – с 28–34 долл/т руды до 16,64 долл/т. Метод оставления целиков из безрудных интервалов позволяет: 1 – отказаться от породной и твердеющей закладки со снижением удельных затрат до 5,18 долл/т руды; 2 – управлять горным давлением при разработке жильных тел на вертикальный размах каскадами до 120 м, при ожидаемых глубинах вскрытия оруденения до 1000 м; 3 – повысить качество эксплуатационной руды за счет минимизации первичного разубоживания от безрудных интервалов с 14 до 25%.

Ключевые слова: жильное месторождение, инвариантность блоков, создание геотехнических условий рудных интервалов, создание геотехнических условий безрудных интервалов, породные целики, удельные затраты

Для цитирования: Ермошкин Д.Н., Курманалиев К.З., Мансуров В.А., Межеловский В.И., Бабкин Е.А. Обоснование применимости мозаичной системы целиков в безрудных блоках при отработке жильных месторождений золота. Горная промышленность. 2023;(3):108–114. https://doi.org/10.30686/1609-9192-2023-3-108-114

Информация о статье

Поступила в редакцию: 11.04.2023

Поступила после рецензирования: 05.05.2023

Принята к публикации: 10.05.2023

Информация об авторах

Ермошкин Денис Николаевич – генеральный директор, Global Asia Management, г. Бишкек, Кыргызская Республика

Курманалиев Капар Зарлыкович – горный инженер-геолог, Геолэкспертпроект, г. Бишкек, Кыргызская Республика; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Мансуров Владимир Аглеевич – доктор физико-математических наук, профессор, советник по геотехнике, Vertex Gold Co, г. Бишкек, Кыргызская Республика

Межеловский Виктор Игоревич – генеральный директор, Глобал Ширальджин Майнинг, г. Бишкек, Кыргызская Республика

Бабкин Евгений Анатольевич – руководитель геотехнического департамента, Vertex Gold Co, г. Бишкек, Кыргызская Республика

Введение

Размерности безрудных и некондиционных перерывов внутри контура оруденения, измеренные на различном уровне по фрактальности и линейной степенной иерархии безрудных блоков, позволяют прогнозировать и выделять подобные образования для создания системы целиков.

Актуальность задачи определяется внедрением системы разработки месторождения укрупненными эксплуатационными блоками до 120х120 м. В первую очередь это связано с поддержанием параметров очистных пространств породными целиками без потерь руды. Предлагаемая геотехнология нуждается в детализации и внедрении в связи с геологическими прогнозами развития оруденения по вертикали до 1000 м и наличием открытых очистных пространств при применяемой в настоящее время системе очистных работ с открытым пространством и магазинированием руды.

Цель работы – рассмотрение геомеханических условий возможности формирования целиков в укрупненных эксплуатационных блоках. Для этого необходимо определить параметры напряженно-деформационного состояния целиков и очистного контура и обосновать методику выделения безрудных и некондиционных интервалов (блоков) под целики.

Дискретность оруденения и ячеистой структуры контуров запасов

Развитие структурно-динамических систем эндогенных месторождений, отличается от процессов формирования обычных структур, не связанных с процессами гидротермального рудообразования. В настоящее время все больше данных указывает на то, что структуры рудных полей не возникают задолго до отложения в них руд, как считали ранее, а формируются почти одновременно с процессами рудообразования и активно контролируют как перенос, так и отложение рудного вещества [1]. Такой режим обусловлен сейсмическими процессами, происходящими во флюидизированных средах. Результаты влияния сейсмодинамических эффектов на миграцию флюидов, проницаемость тектонических проводников получены [2–7] при изучении орогенных золоторудных месторождений Австралии и Канады.

Согласно геотехнике при развитии ячеистой с инвариантными блоками системы геологической среды выделяются два момента:v Дезинтеграция и разуплотнение / дилатансия среды / массива горных пород определяются составляющими системы, в которой по подсистемам развиваются различающиеся условия нагружения (напряжение и деформация) по включениям жестких или мягких / податливых блоков (stiff and rigid inclusions). В массиве горных пород, включающем податливые / мягкие блоки, при их нагружении со стороны более жесткого массива горных пород преобладает разрушение без динамической составляющей в момент достижения ими предела прочности, что обусловлено накоплением в них трещин. Эти блоки представляют собой трещиноватую среду. В этом случае нагрузка на такие блоки распределяется таким образом, что их нагружение происходит в режиме задаваемых деформаций. А при мягком нагружении, реализуемом в горном массиве, включающем в себя жесткие блоки, вся нагрузка концентрируется на них. А при достижении внешней нагрузкой величины их прочности вся накопленная в окружающем массиве энергия резко разгружается в возникающие трещины или в подготовленный/существующий очаг разрушения с предельной концентрацией в нем трещин или в имеющуюся в структуре трещину Гриффитсовского размера [8], и разрушение протекает хрупко с динамическими проявлениями – выделением энергии. В этом случае нагружение происходит в режиме задаваемых напряжений.

В мягких и жестких включениях / блоках, составляющих некую систему в массиве горных пород, при их нагружении за счет разрушений, происходящих в податливых / мягких блоках, нагрузка перераспределяется на жесткие блоки за счет возникшей новой трещиноватой структуры породы в податливых блоках. Эта нарушенная порода представляет собой систему, которая еще несет нагрузку, но податливо деформируется за пределом ее прочности, расходуя подводящуюся энергию/нагрузку на деформации за счет развития структуры и ее дальнейшего перехода на низший иерархический уровень [9; 10].

Развитие оруденения по зонам трещиноватости формируется как подсистемы линз, гнезд, малых рудных столбов и соответствующих по размерности безрудных интервалов (инвариантность включений жестких и мягких блоков) – по подсистемам трещиноватости, которые, в свою очередь, формируют барьер (давление–температура) разгрузки флюидов, схематически это представлено на рис. 1.

Рис. 1 Теневые структуры напряжений Источник: [7]

Fig. 1 Shadow stress structures Source: [7]

Размерность иерархических блоков оруденения по простиранию в целом подчиняется степенной функции с включениями подсистем крупных, средних, мелких рудных столбов; иерархии от крупных, средних, мелких линз до гнезд оруденения, в том числе безрудные и не кондиционные интервалы, пережимы. Фрактальная размерность блоков и оруденения иерахически подобны. Системы блоков по простиранию от участка рудного тела (морфологический рудный столб – крупный – до 111 (слева) и 94 м (справа), рис. 2) – состоят из перечисленных рудных и безрудных подсистем и по размерности выражаются степенным коэффициентом, рис. 2, по Садовскому: i – целые числа [11].

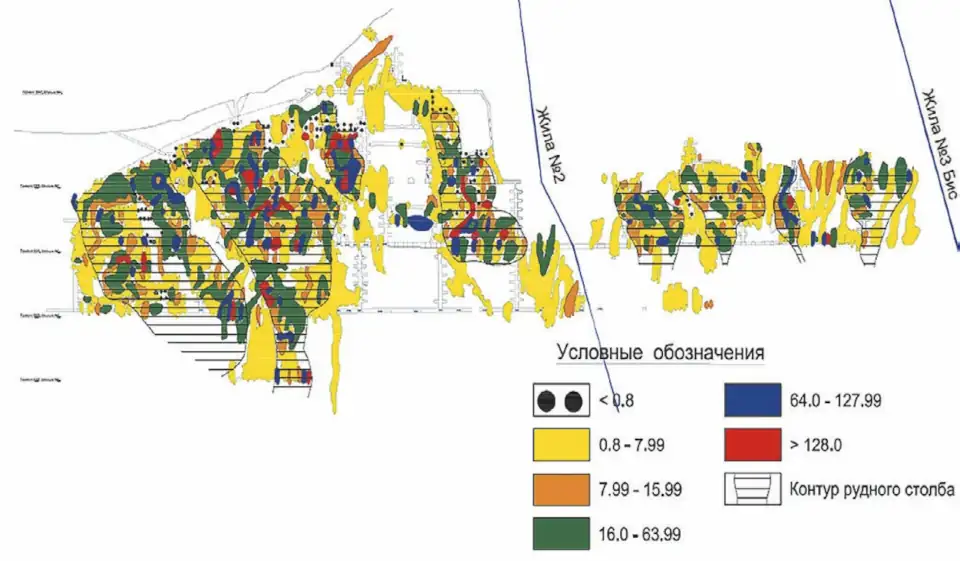Рис. 2 Подсистемы оруденения рудного тела №2бис. Слева участок ЮЗ, справа СВ. Штриховкой и цветовым крапом выделены средние рудные столбы, цветовым крапом – мелкие рудные столбы, линзы и гнезда изоконцентрат оруденения

Fig. 2 Mineralization subsystems of No.2bis ore body. The southwest section is on the left, the northeast section is on the right. Hatching and color speckles indicate medium-size ore pillars; color speckles indicate small-size ore pillars, lenses and pockets of mineralization

Линейные размеры определены как L = √Lh · Ll, линейные размеры в метрах по простиранию Ll и падению Lh блоков по подсистемам [12]. Таким же образом исчислены и безрудные перерывы по блокам. Отношения между подсистемами по степени Li / Li + 1 безрудных блоков, табл. 1, рис. 3. Распространение и размерность безрудных перерывов подчеркивается соотношением фрактальных размеров рудных образований и измеренных безрудных перерывов в контуре оруденения (морфологический рудный столб, рис. 2) [5], соответственно, фрактальная размерность составляет: Dруд = 1,11; Dбезруд = 1,04. Расхождение может объясняться некоторым искажением при прорисовке рудных концентраций содержаний золота.

Таблица 1 Линейные размеры подсистем оруденения и безрудных, некондиционных перерывов

Table 1 Linear dimensions of the ore and ore-free subsystems and substandard ore intervals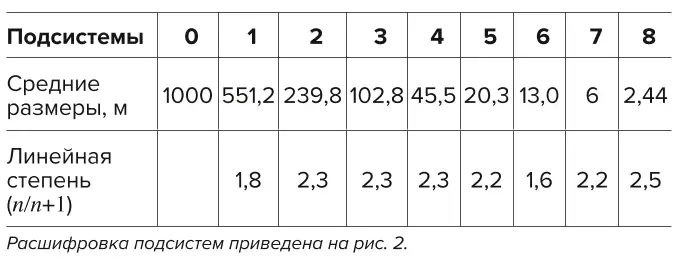

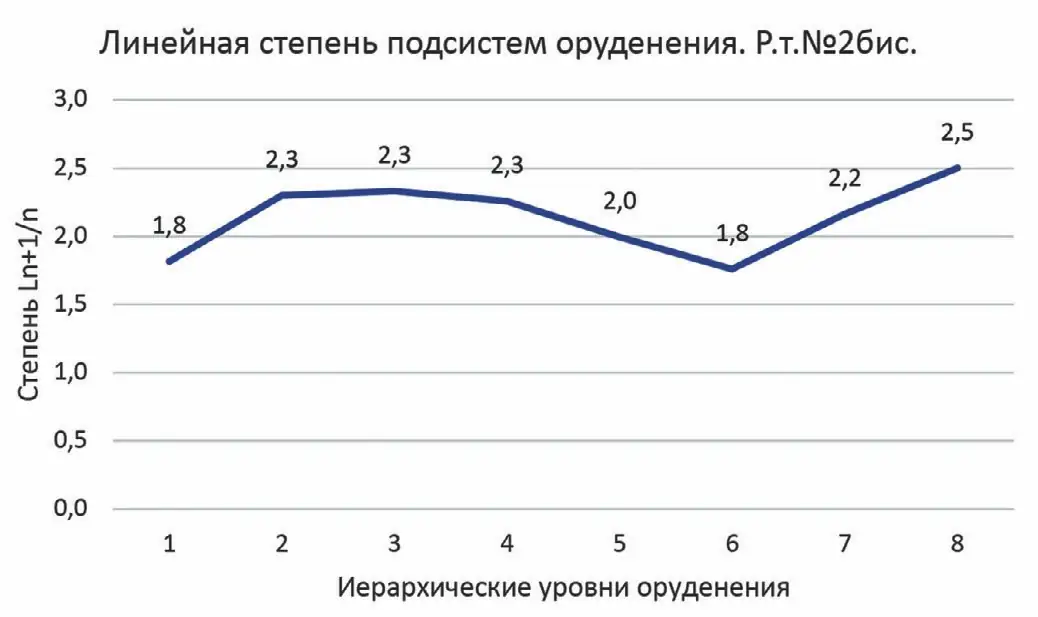Рис. 3 График линейной степени отношения рудных подсистем по иерархии: от жильной зоны №2бис, 1 – рудное тело №2бис; 2 – морфологические рудные столбы (участки); 3 – средние рудные столбы (концентрационные); 4 – мелкие рудные столбы; 5 – крупные линзы; 6 – мелкие линзы; 7 – крупные гнезда; 8 – мелкие гнезда

Fig. 3 A hierarchy chart of the linear extent of ore subsystems ratio from No. 2bis vein zone: 1 – No. 2bis ore body; 2 – morphological ore pillars (sections); 3 – medium-size ore pillars (concentration); 4 – small-size ore pillars; 5 – large-size lenses; 6 – small-size lenses; 7 – large-size pockets; 8 – small-size pockets

Геомеханические условия очистного пространства

Действующая система очистных работ с открытым очистным пространством и магазинированием руды, приняты параметры: высота блока принята равной высоте этажа и равна в среднем 40 м (до 60 м). По простиранию рудное тело разделяется на выемочные блоки вентиляционно-ходовыми восстающими через 40 м.

Управление горным давлением осуществляется с помощью целиков, параметры которых приняты по данным расчета. В процессе производства работ применяются целики [13; 14]: межкамерные по высоте 4–6 м, по ширине 5–6 м. Потолочины 6 м на всю длину эксплуатационного блока. После отработки смежных блоков межкамерные целики отрабатываются полностью, потолочины сокращаются до 3,1 м. Параметры целиков рассчитаны исходя из традиционного допущения по критерию – нагрузка не превышает несущую способность целиков при сжатии:

. (1)

Действующие напряжения в целиках определяются из выражения

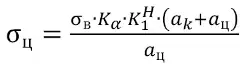. (2)

Несущая способность целиков зависит от прочности пород на сжатие, их трещиноватости, формы целика:

, (3)

где σсж – прочность пород на сжатие, МПа; Kтр – коэффициент трещиноватости;

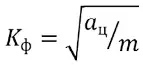– коэффициент формы;  (4)

aц – ширина целика, м; m – мощность жилы, м. Исходя из условия прочности ширину междукамерных целиков определяют по формуле:

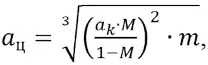(5)

где

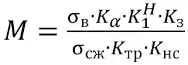, (6)

где σ_сж – прочность пород на сжатие, МПа; K₁^H– коэффициент нагрузки на междукамерный целик; K_тр – коэффициент трещиноватости; K_нс – коэффициент изменения несущей способности целика за счет проходки восстающего и смотровых окон.

Коэффициент нагрузки учитывает распределение давления от вмещающих пород на междукамерные целики и зависит от формы и размеров камер. Его значение

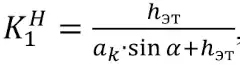, (7)

где h_эт – высота этажа, м. Коэффициент K_нс учитывает уменьшение несущей способности целика за счет проходки восстающего и смотровых окон. Коэффициент трещиноватости K_тр зависит от направления трещин в целике.

Действующие напряжения в потолочинах определяют из выражения

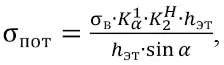(8)

ее толщину исходя из условий прочности

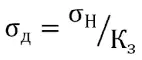(9)

по формуле

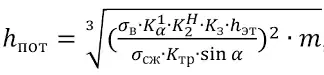, (10)

где – K₂^H коэффициент нагрузки на потолочину; K_a¹– коэффициент влияния угла падения залежи на загруженность потолочины; h_эт – высота этажа, м. Коэффициент учитывает распределение давления от вмещающих пород на потолочину, его находят из:

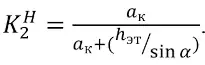. (11)

Полученные данные в соответствии с геотехническими условиями месторождения приведены выше. Устойчивые параметры обнажений определены по формуле:

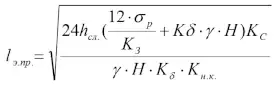, (12)

где h_cл. – мощность несущего слоя пород, слагающих висячий бок, м; σ_p – прочность пород кровли на разрыв, т/м²; К₃ – коэффициент запаса прочности; γ – объемный вес пород, т/м³; Н – глубина, м; К_н.к. – коэффициент пригрузки на висячий бок; К_c – коэффициент структурного ослабления; К_Б – коэффициент бокового давления.

При характеристиках вмещающих гранитов устойчивость пролетов и высота камеры определена в 54,3 м при 60 м высоты. За 12 лет эксплуатации рудника (более 200 эксплуатационных блоков) катастрофических сдвижек не отмечалось.

Внедряемая система очистных работ: слоевая из подэтажных штреков через 13 м, с механизированным бурением и откаткой до и по участковому рудоспуску, доступом на подэтажи из транспортных уклонов через орты, размеры эксплуатационного блока h = 80–120 м х до l = 120–160 м, рис. 3.

Для отдельных крупных линз с бонанцево-рудностолбовым (> 32 г/т) и бонанцевыми (> 64) содержаниями золота предусмотрена селективная отработка с системой слоевой, почво-, потолкоуступной.

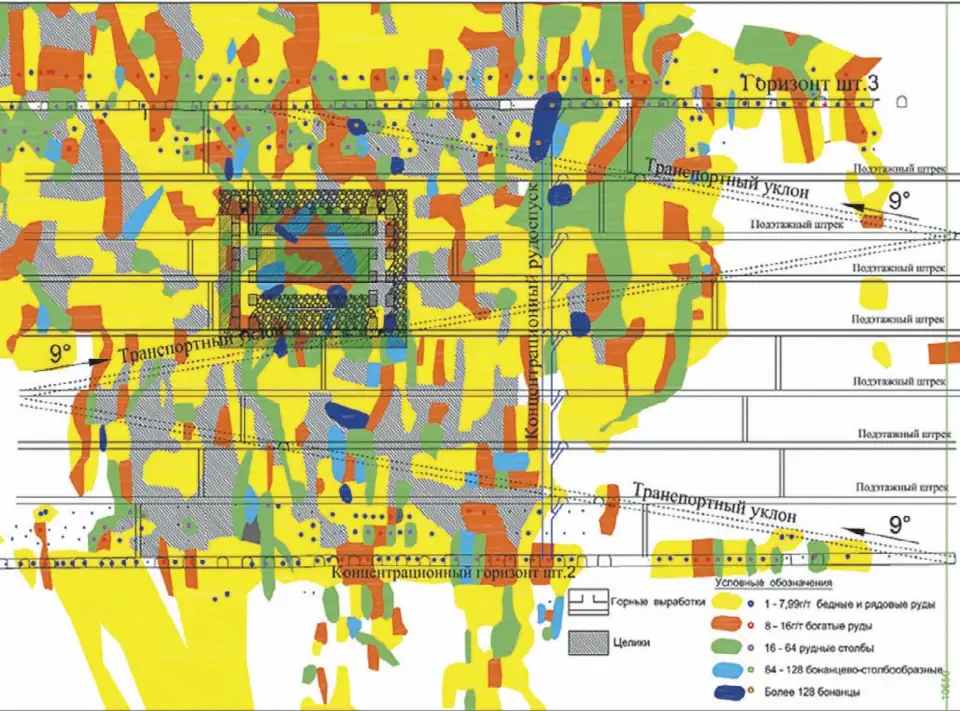Рис. 4 Схематический продольный план комбинированной системы очистных работ – слоевая, из подэтажных штреков, с механизированными бурением и откаткой

Fig. 4 A schematic longitudinal map of a combined longwall system: cut-and-fill sublevel stoping with mechanized drilling and haulage

При рассматриваемой системе очистных работ предусматривается выделение на основе вышеприведенных критериев безрудных и некондиционных интервалов в целики. Параметры последних составляют от 5–6 до 8–10 м по простиранию и до 13–26 м по высоте, без пересечения подэтажного штрека. Для межэтажного перекрытия предусматривается устройство целиков потолочин, над- или под- этажным штреком в виде цепочек толщиной до 3 м, длиной до 10–20 м. Расстояние между этажными потолочинами пропорционально расположению подэтажных штреков до 26–52 м – для исключения вывалов руды и породы на нижние этажи. Формирование Т-образных целиков на сочленении с потолочиной предусматривается исходя из однородности целика с потолочиной, которые при нагрузках деформируются как в продольном, так и поперечных направлениях. Сдвиг в поперечном направлении сдерживается потолочиной. В результате у контакта с потолочиной образуется клиновидная область всестороннего сжатия, являющаяся наиболее устойчивой частью целика [5; 15–18].

Расчетный объем безрудных перерывов в контуре оруденения и эксплуатационного блока составляет от 14 до 25% по площади на вертикальную проекцию. Локализация ячеистая, близка к равномерной по площади блока. Для действующей системы очистных работ объем оставляемых целиков потолочин до 7,5% от объема блока.

Для укрупненного эксплуатационного блока в качестве основы при вычислении устойчивости междуэтажных целиков и обнажений очистных камер принята зависимость напряжений вокруг выработок [6; 13; 15; 19]:

σ_i = σ_Y, + σ_X= σ_в k_yi + σ_г k_xi, (13)

где σ i – полное напряжение в i-й точке контура выработки, МПа; σ_Y, σ_X – соответственно вертикальные (ось Y) и горизонтальные (ось X) напряжения на контуре выработки; σ в, σг – вертикальное и горизонтальное первоначальные (природные) напряжения горного массива, МПа; k_yi, k_xi – коэффициенты концентрации соответственно вертикального и горизонтального напряжений от единичных нагрузок в i-й точке контура выработки. На основе этого составлена модель по 54 месторождениям золота в тонких жилах с расчетом коэффициента техногенных напряжений вокруг очистных камер К_х и К_у соответственно горизонтальных и вертикальных (стенки камер), по мощностям жильных тел и углам падения 60, 75, 90° (рис. 5) [10].

Рис. 5 Коэффициенты K_x и K_u: а – в стенке и б – в кровле очистной камеры при угле наклона жилы к горизонту 75⁰ при различной выемочной мощности в условиях отработки одного этажа; 1, 2, 3 – выемочные мощности рудного тела, м Источник:[10]

Fig. 5 The K_x and K_u factors: а – in the side wall and б – in the roof of the stope at the lode dip angle of 75⁰ at different mined thickness for single-level mining; 1, 2, 3 – mined thickness of the ore body, m Source:[10]

Коэффициенты концентраций напряжений в кровле (потолочинах) камер и междукамерном целике по знаку положительные, т.е. полученные по ним напряжения носят сжимающий характер. В стенках же камер они отрицательные. При увеличении мощности растягивающие напряжения в стенках падают, а в кровле напряжения увеличиваются. Метод применим как физико-механическая модель расчета устойчивости целиков и обнажений камер для оценки устойчивости элементов системы разработки [10; 20]. Представленная модель используется для оценки управления геомеханическими процессами в очистном пространстве в целиках и межцеликовых пространствах выработок (системы целик–очистная камера).

Обсуждения

Вероятно, безрудные интервалы, предусмотренные для формирования целиков, происходят из первоначальных условий образования, по инвариантным включениям, жестких и мягких блоков с различающейся компетентностью физико-механических свойств по отношению к системе напряжение–деформации (НДС). Образование «теневых структур напряжений» с пониженным развитием трещиноватости создавало отрицательные области для разгрузки рудного вещества из флюидов, т.е. напряжения как бы обтекали эти своеобразные области в блочной системе на синрудном этапе. По этому критерию подобные области могут выражаться и как подсистемы блоков инвариантности НДС, и на последующих этапах тектогенеза (альпийского). И их можно оценить как оптимальные блоки для создания устойчивых целиков.

Для изучения этого процесса планируются исследования устойчивости и трещиноватости по существующим целикам и деформациям за период 1–3–5–10 лет.

Это позволит для системы предложенных целиков в дальнейшем использовать моделирование их геомеханических свойств, в том числе с оценкой концентраций напряжений в укрупненном очистном пространстве по локализации, размерам, единству с потолочинами и форме целиков.

Заключение

Удельные эксплуатационные затраты за счет снижения затрат на буровзрывные работы, откатку объема целиков (до 14%) на горно-подготовительные и очистные работы составляют – 16,64 долл/т, против существующей 28–34 долл/т руды.

• Метод оставления целиков из безрудных интервалов позволяет отказаться от породной и твердеющей закладки со снижением удельных затрат до 5,18 долл/т руды.

• Метод позволяет управлять горным давлением при разработке жильных тел на вертикальный размах каскадами до 120 м, при ожидаемых глубинах вскрытия оруденения до 1000 м.

• Метод позволяет повысить качество эксплуатационной руды за счет минимизации первичного разубоживания от безрудных интервалов с 14 до 25%.

Список литературы

1. Старостин В.И., Дергачев А.Л., Семинский Ж.В. Структуры рудных полей и месторождений. M.: Изд-во МГУ; 2002. 352 с.

2. Cox S.F. Coupling between deformation, fluid pressure and fluid flow in ore-producing hydrothermal systems at depth in the crust. Economic Geology: Bulletin of the Society of Economic Geologists. 2005;100:39–75. Available at: https://www.eoas.ubc.ca/sites/default/files/user/khickey/Week02/Cox_100_Econ_Geol_2005.pdf

3. Huang Z., Dai X., Dong L. Buckling failures of reserved thin pillars under the combined action of in-plane and lateral hydrostatic compressive forces. Computers and Geotechnics. 2017;87:128–138. https://doi.org/10.1016/j.compgeo.2017.02.013

4. Кузин А.М. Месторождения полезных ископаемых, землетрясения и методология интерпретации сейсмических данных. Труды Ферсмановской научной сессии ГИ КНЦ РАН. 2019;(16):323–327. https://doi.org/10.31241/FNS.2019.16.065

5. Nguyen P.T., Harris L.B., Powell C.McA., Cox S.F. Fault-valve behaviour in optimally oriented shear zones: an example at the Revenge gold mine, Kambalda, Western Australia. Journal of Structural Geology. 1998;20(12):1625–1640. https://doi.org/10.1016/S0191-8141(98)00054-6

6. Sibson R.H. Earthquake rupturing as a mineralizing agent in hydrothermal systems. Geology. 1987;15 (8):701–704. https://doi.org/10.1130/0091-7613(1987)15<701:ERAAMA>2.0.CO;2

7. Sibson R.H., Skott J. Stress/fault controls on the containment and release of overpressured fluids: Examples from gold-quartz vein systems in Juneau, Alaska; Victoria, Australia and Otago, New Zealand. Ore Geology Reviews. 1998;13(1-5):293–306. https://doi.org/10.1016/S0169-1368(97)00023-1

8. Нотт Дж.Ф. Основы механики разрушения. [пер. с англ. Д.В. Лаптева, под ред. В.Г. Кудряшова]. М.: Металлургия; 1978. 256 с.

9. Brady B.T. The nonlinear mechanical behavior of brittle rock Part II — Stress-strain behavior during regions III and IV. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1969;6(3):301–310. https://doi.org/10.1016/0148-9062(69)90007-2

10. Сосновская Е.Л. Оценка техногенных напряжений на контуре очистных камер при разработке крутопадающих золоторудных жил малой мощности. Вестник Иркутского государственного технического университета. 2014;(12):82–88. Режим доступа: http://journals.istu.edu/vestnik_irgtu/journals/2014/12/articles/13

11. Садовский М.А., Балховитинов Л.Г., Писаренко В.Ф. Деформирование геофизической среды и сейсмический процесс. М.: Наука; 1987. 100 с.

12. Садовский М.А. Естественная кусковатость горной породы. Доклады Академии наук СССР. 1979;247(4):829–831. Режим доступа: https://www.mathnet.ru/rus/dan42895

13. Влох Н.П. Управление горным давлением на подземных рудниках. М.: Недра; 1994. 208 с. Режим доступа: https://www.geokniga.org/bookfiles/geokniga-vloh-np-upravlenie-gornym-davleniem-na-podzemnyh-rudnikah-1994.pdf

14. Макаров П.В. Эволюционная природа блочной организации геоматериалов и геосред. Универсальный критерий фрактальной делимости. Геология и геофизика. 2007;48(7):724–746. Режим доступа: https://www.sibran.ru/upload/iblock/42a/42ae76275048d558a33a8596897ef667.pdf

15. Ведмедев А.В. Коэффициент формы в расчетах подземных сооружений. В кн.: Геотехническая механика [межведомств. сб. науч. тр.]. Днепропетровск; 2004. Вып. 51. С. 250–257.

16. Бутаков Л.И., Зайцев Б.М., Казаченко Ю.А., Коваленко В.И., Кокташев А.Ф., Меринов М.А. и др. Технология разработки золоторудных месторождений. М.: Недра; 1995. 336 с. Режим доступа: https://www.geokniga.org/books/9011

17. Балек А.Е., Панжин А.А., Коновалова Ю.П., Мельник Д.Е. Особенности напряженного состояния горного массива Соколовского железорудного месторождения. В кн.: Валиев Н.Г. (ред.) Инновационные геотехнологии при разработке рудных и нерудных месторождений: сб. докладов 7-й Междунар. науч.-техн. конф., Екатеринбург, 10–11 апреля 2018 г. Екатеринбург: Уральский государственный горный университет; 2018. С. 256–264.

18. Харисов Т.Ф., Харисова О.Д. Геомеханическое обоснование параметров устойчивых камер и целиков в сложных горно-геологических условиях. Известия Томского политехнического университета. Инжиниринг георесурсов. 2019;330(7):25–33. https://doi.org/10.18799/24131830/2019/7/2173

19. Ребецкий Ю.Л. Современное состояние теорий прогноза землетрясений. Результаты оценки природных напряжений и новая модель очага землетрясений. В кн.: Яковлев Ф.Л., Арефьева Т.П. (ред.) Проблемы тектонофизики. К сорокалетию создания М.В. Гзовским лаборатории тектонофизики в ИФЗ РАН. М.: Институт физики Земли им. О.Ю. Шмидта РАН; 2008. С. 359–395. Режим доступа: https://www.geokniga.org/books/6034

20. Sepehri M., Apel D., Liu W. Stope stability assessment and effect of horizontal to vertical stress ratio on the yielding and relaxation zones around underground open stopes using empirical and finite element methods. Archives of Mining Sciences. 2017;62(3):653–669. https://doi.org/10.1515/amsc-2017-0047