Анализ напряженно-деформированного состояния моделей разрывных нарушений

Д.Ж. Акматов, А.М. Кулешов, В.Н. Чадин, А.Г. Богачук, К.А. Колесников
Национальный исследовательский технологический университет «МИСИС», г. Москва, Российская Федерация
Горная Промышленность №5 / 2023 стр. 119-123

Резюме: В статье представлен анализ процедуры создания трехмерных моделей разрывных нарушений и тектонических разломов для задач численного моделирования методом конечных элементов. При геомеханическом анализе напряженно-деформированного состояния разломов возникает ряд неопределенностей, связанных с выбором их типа расчетно-геологической модели (дислокационной, доменной, зоны динамического влияния). Выполнен сравнительный анализ напряженно-деформированного состояния указанных расчетно-геологических моделей. Геологическая и структурная модели формируются на основе данных геологического опробования исследуемого участка. Особое внимание уделяется построению структурно-тектонической модели с учетом разрывных нарушений и тектонических разломов, оказывающих влияние на деформации и напряжения породного массива. В результате из трех приведенных вариантов наиболее предпочтительной является расчетно-геологическая модель с зоной динамического влияния. Домен зоны динамического влияния с пониженными физико-механическими свойствами позволяет охватить весь потенциальный объем зоны разрывного нарушения.

Ключевые слова: трехмерные модели, численное моделирование, напряженно-деформированное состояние, разрывные нарушения, разломы, геологическая модель, структурная модель, тектонические блоки, влияние разломов

Для цитирования: Акматов Д.Ж., Кулешов А.М., Чадин В.Н., Богачук А.Г., Колесников К.А. Анализ напряженнодеформированного состояния моделей разрывных нарушений. Горная промышленность. 2023;(5):119–123. https://doi.org/10.30686/1609-9192-2023-5-119-123

Информация о статье

Поступила в редакцию: 26.07.2023

Поступила после рецензирования: 06.09.2023

Принята к публикации: 18.09.2023

Информация об авторах

Акматов Дастан Женишбекович – аспирант кафедры геологии и маркшейдерского дела, Горного института НИТУ МИСИС, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Кулешов Артем Михайлович – аспирант кафедры геологии и маркшейдерского дела, Горного института НИТУ МИСИС, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Чадин Владимир Николаевич – аспирант кафедры геологии и маркшейдерского дела, Горного института НИТУ МИСИС, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Богачук Анатолий Григорьевич – аспирант кафедры геологии и маркшейдерского дела, Горного института НИТУ МИСИС, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Колесников Константин Александрович – аспирант кафедры геологии и маркшейдерского дела, Горного института НИТУ МИСИС, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

При выполнении численного моделирования напряженно-деформированного состояния (НДС) в сложных геологических структурах подготовка геометрических данных для модели и определение зон с различными физико-механическими характеристиками являются наиболее трудоемким этапом [1–5]. Особенно важной частью этого процесса является подготовка расчетно-геологических и каркасных моделей для численного моделирования, включая описание геометрических параметров объектов и структур [1; 5]. Также значительное внимание уделяется определению доменов с различными физико-механическими свойствами, так как различные геологические образования могут обладать разной прочностью, текучестью и другими характеристиками [2; 6].

В данном контексте тектонические нарушения представляют собой объемные зоны с определенной мощностью, которая зависит от масштаба данного нарушения. Они могут включать в себя разнообразные структуры и формы структурных деформаций, которые могут значительно влиять на поведение геологической среды в условиях нагрузок и деформаций [7–11].

Исходя из этого качественная подготовка геометрических данных и учет физико-механических свойств различных зон играют решающую роль в точности и достоверности численных моделей сложных геологических структур при анализе их поведения в условиях динамических и статических нагрузок.

Расчетно-геологические модели разрывных нарушений

Разработка расчетно-геологической модели выполняется в два этапа. Во-первых, создается каркасная геологическая модель, которая представляет подповерхностную структуру в районе модели. Данная геологическая модель создается на основе геолого-геофизических данных [6]. На втором этапе создается модель со структурными особенностями в виде разрывных нарушений и их зон влияния (рис. 1).

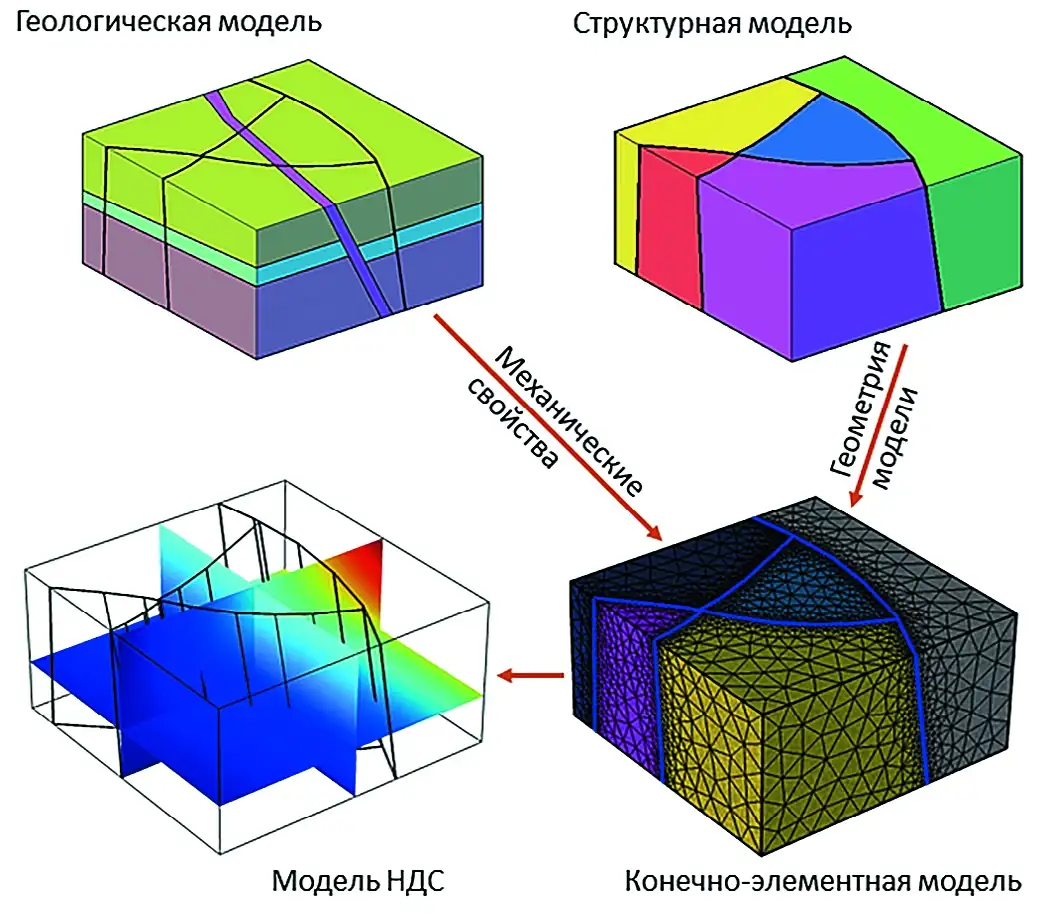Рис. 1 Алгоритм построения трехмерной геомеханической модели

Fig. 1 Algorithm for building a 3D geomechanical model

Для разработки дизайна объемной геомеханической модели необходимо обосновать метод построения каркасной расчетно-геологической модели [5–6]. Для этого были созданы три тестовые модели каркасов расчетно-геологических элементов (рис. 2), включающих в себя тектонические разломы, блоки и зоны динамического влияния. Представленные тестовые модели показывают три основных подхода к каркасному моделированию расчетно-геологических элементов (РГЭ):

1. Использование структурно-тектонической модели: В этом подходе структурно-тектоническая модель принимается в качестве РГЭ без ее предварительного изменения. Это означает, что элементы структурно-тектонической модели нумеруются как расчетно-геологические элементы и им присваиваются соответствующие физико-механические свойства (рис. 2, а).

2. Использование структурно-тектонических блоков: В этом подходе в качестве РГЭ используются структурно-тектонические блоки, границы которых являются дислокациями, а не объемными телами. Такой подход также предполагает решение задачи взаимодействия между структурно-тектоническими блоками (рис. 2, б).

3. Использование укрупненных инженерно-геологических тел: В этом подходе РГЭ представляют собой укрупненные инженерно-геологические тела, которые имеют однородные физико-механические свойства. В данном случае разломы интерпретируются как зоны динамического воздействия, в соответствии с зависимостями, описанными для тектонических нарушений (рис. 2, в) [6].

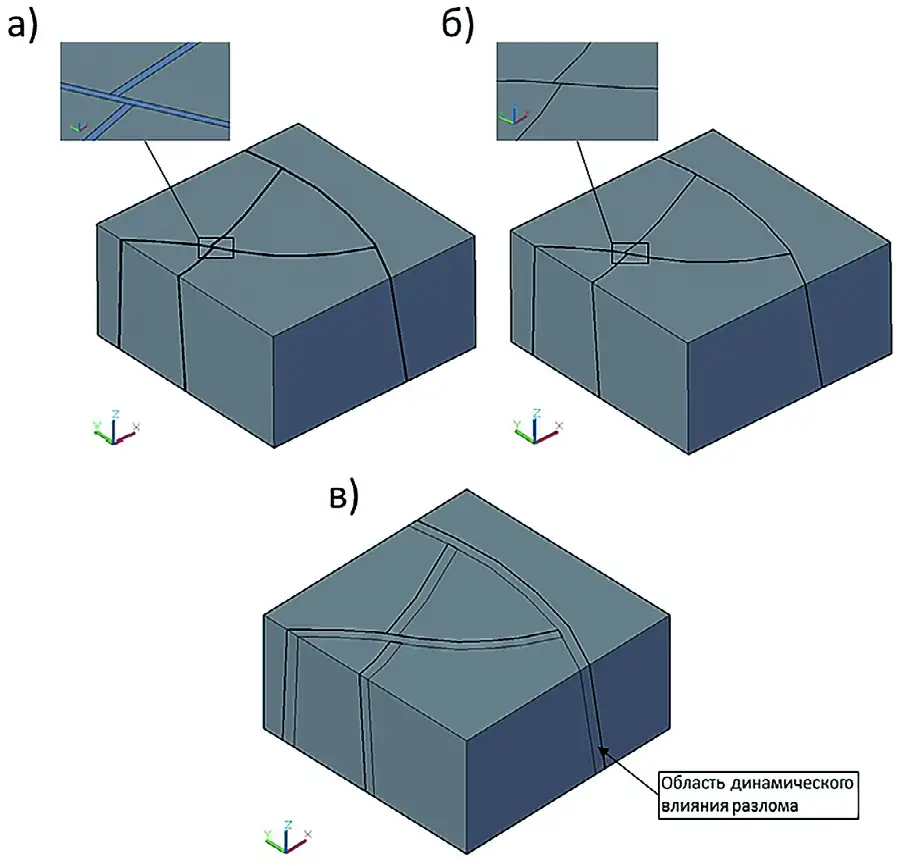Рис. 2 Тестовые каркасные модели расчетно-геологических элементов при геомеханическом моделировании в ГГИС: а – все структуры заданы в виде блоков по геологическим данным; б – тектонические блоки по линии разломов (домены по блокам разлома); в – тектонические блоки и область динамического влияние разломов

Fig. 2 Test wire-frame models of computational geological elements in geomechanical modeling in the mining-andgeological information system: а – all structures are defined as blocks according to geological data; б – tectonic blocks along the fault line (domains according to the fault blocks); в – tectonic blocks and the area of the fault dynamic impact

Представленные тестовые расчетно-геологические модели иллюстрируют различные методы представления тектонических разломов и блоков в объемной модели. Эти методы включают использование объемных тел разломов с физико-механическими свойствами, представление разломов в виде дислокаций в рамках тектонических блоков и расчет динамического влияния разломов для определения ослабленных областей. Каждый из этих подходов имеет свои особенности и позволяет учесть разные аспекты влияния тектонических структур на поведение геологической среды при численном моделировании [9–10].

Численное моделирование напряженно-деформированного состояния

Методом конечных элементов выполнено многовариантное моделирование НДС для всех трех типов расчетно-геологических моделей разрывных нарушений. Размеры и компоновка конструкции показаны на рис. 3. Размеры модели 2000×2000×1000 м. Граничные условия задавались идентично для всех вариантов моделей с одинаковыми показателями внешнего давления. В качестве нагрузок задавалось гравитационное давление, боковой распор по А.Н. Диннику и дополнительное тектоническое давление по бокам модели: σH = 10 МПа, σh = 7 МПа. На рис. 3 представлена ориентация действующих главных напряжений.

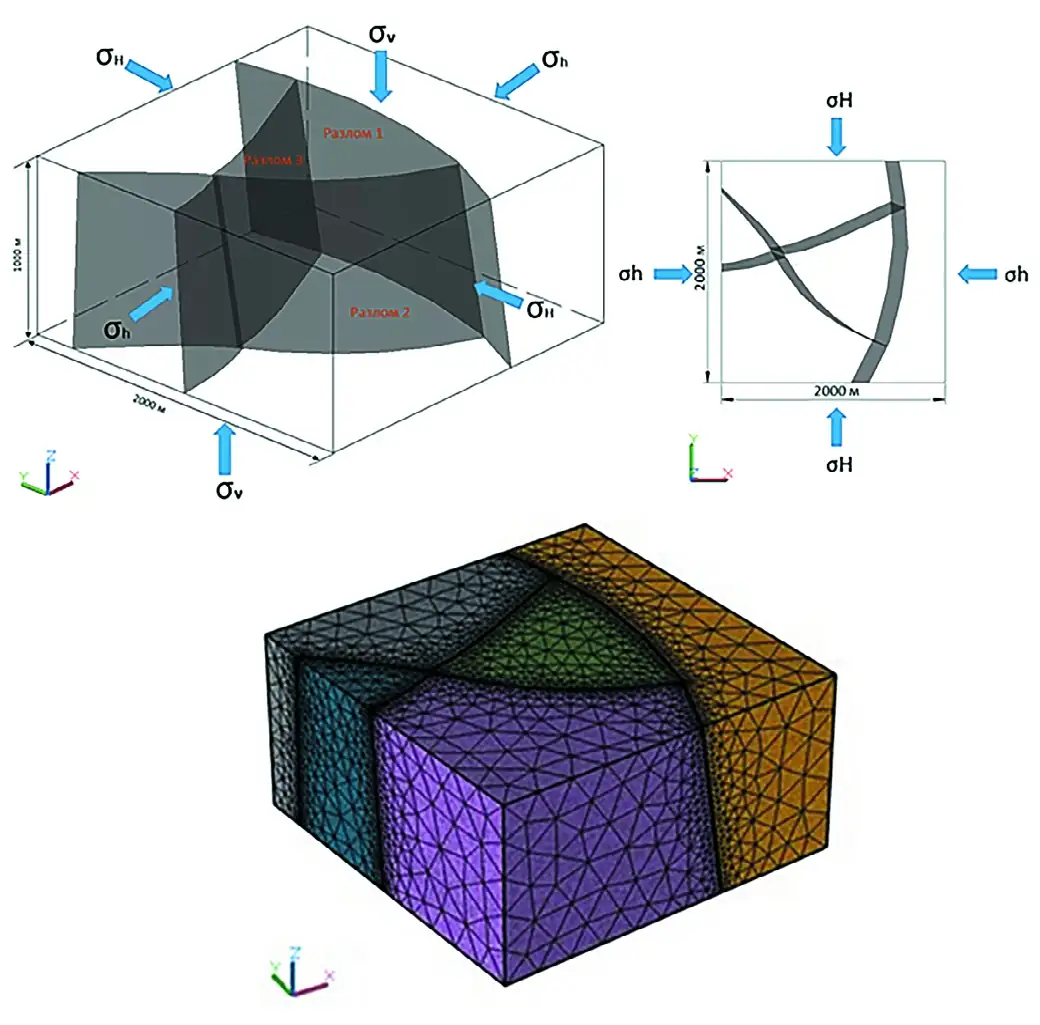Рис. 3 Граничные условия расчетно-геологической модели

Fig. 3 Boundary conditions of the computational geological model

Создание численной модели с использованием метода конечных элементов реализовано в программном обеспечении COMSOL Multiphysics 6.0. При определении геометрии и параметров разбиения сетки конечных элементов контролировалась плотность конечных элементов (см. рис. 3) для сохранения вычислительной эффективности, при условии вычислительной сходимости модели. На рис. 3 показана модель сетки конечных элементов, которая включает в себя около 250 000 элементов. Это количество элементов представляет собой компромисс между точностью расчетов и вычислительной эффективностью.

Получены результаты по трем вариантам модели (рис. 4). На рис. 4, а видно, что аномалии напряжений проявляются в результате разрывных нарушений, связанных с тектоническими блоками. В зоне контакта двух доменов наблюдается переходная зона с высокими значениями напряжений, в то время как в зонах разрывных нарушений напряжения резко снижаются до нулевых значений.

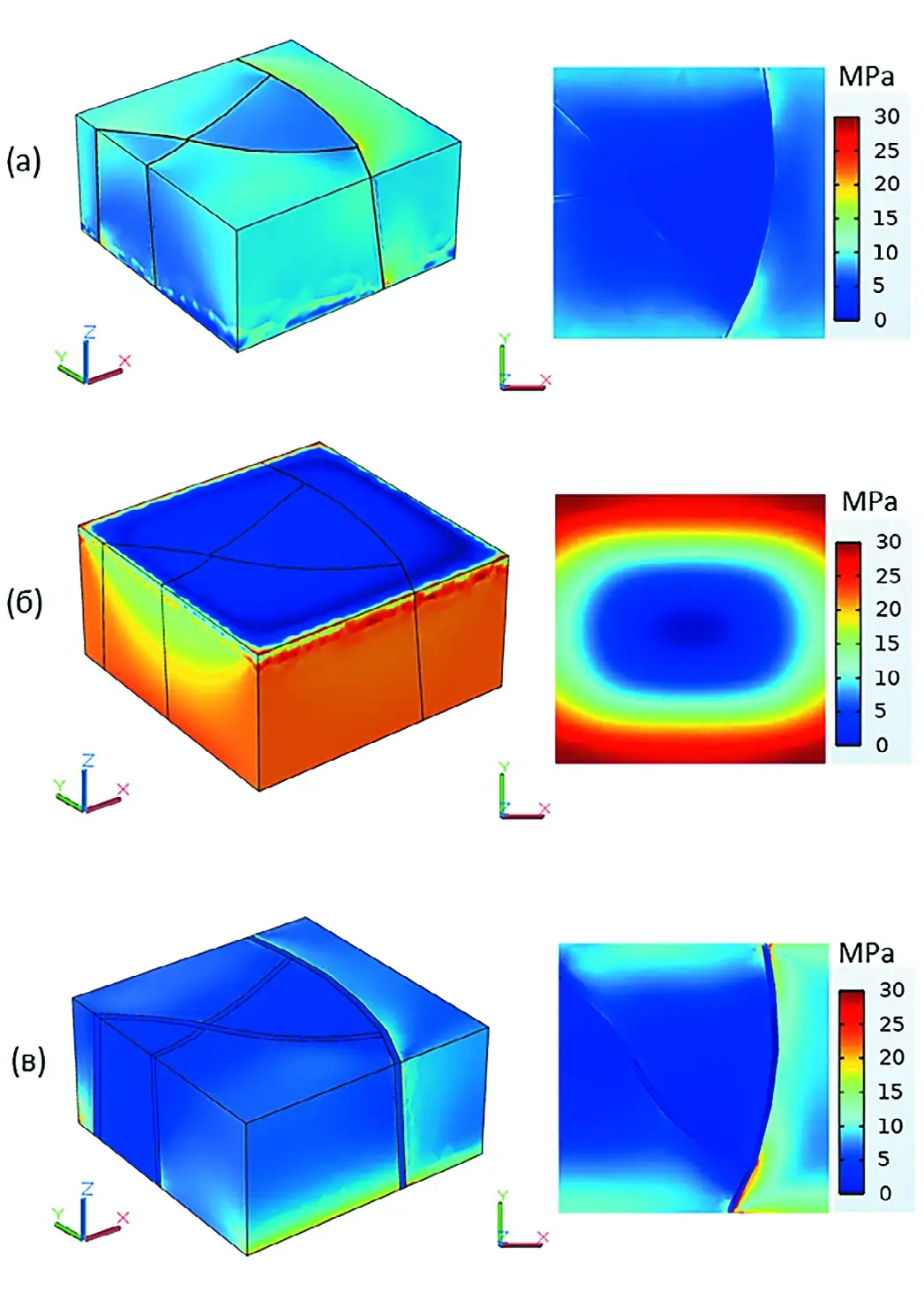Рис. 4 Распределение интенсивности напряжений для тестовых каркасных моделей: а – тектонические блоки по линии разломов (домены по блокам разлома); б – все структуры заданы в виде блоков по геологическим данным; в – тектонические блоки и область динамического влияния разломов

Fig. 4 Distribution of the stress intensity for the test wire-frame models: а – tectonic blocks along the fault line (domains according to the fault blocks); б – all structures are defined as blocks according to geological data; в – tectonic blocks and the area of the fault dynamic impact

Это явление при анализе данных может свидетельствовать о том, что в зонах разломов происходят интенсивные деформационные процессы. На рис. 4, б видно, что между тектоническими блоками отсутствует переход напряжений. Это происходит потому, что разрывные зоны, представленные в виде дислокаций, не имеют объема и, как следствие, не вносят изменения в баланс напряженнодеформированного состояния. Отсутствие перехода напряжений между блоками указывает на то, что деформационные процессы не проникают внутрь разрывных зон, так как эти зоны не имеют объемных характеристик, способных изменять напряженно-деформационное состояние в соседних блоках. Изображение на рис. 4, в показывает перераспределение напряжений, аналогичное первому варианту (см. рис. 4, а), однако с учетом зон влияния разломов и опасных деформационных зон.

Эта модель является более оптимальным вариантом, так как она учитывает нестабильные зоны влияния разломов. Учет зон влияния разломов и опасных зон наведенной трещиноватости позволяет более точно оценить воздействие тектонических структур на распределение напряжений в геологической среде. Это важно для определения зон потенциальных деформаций, где интенсивные деформационные процессы могут привести к нестабильности горных массивов.

Такие наблюдения подчеркивают значимость учета физико-механических свойств разрывных зон при моделировании и анализе деформационных процессов, так как они могут оказывать существенное влияние на взаимодействие между горными блоками и формирование напряженно-деформационных полей в геологической среде.

Выводы

В результате анализа трех вариантов расчетно-геологических моделей получены различные распределения напряженно-деформированного состояния по линиям разломов и стыков тектонических блоков. Результаты показывают, что зоны разрывных нарушений в моделях, представленных в виде зон динамического влияния, могут иметь существенное влияние на распределение напряжений и деформационное состояние в соседних блоках. Учет зон влияния разломов и опасных деформационных зон позволяет более точно определить потенциальные зоны деформаций и прогнозировать нестабильность массивов горных пород. В целом анализ этих результатов подчеркивает важность учета зон влияния разломов при моделировании и анализе напряженно-деформационного состояния горных массивов, так как эти факторы могут существенно влиять на их стабильность и поведение.

Список литературы

1. Акматов Д.Ж., Евлоев Х.Ю., Меллер А.Д., Манукян Т.А., Чадин В.Н. Методика численного моделирования полей напряжений в районе размещения угольных шахт. Горная промышленность. 2023;(1):39–44. https://doi.org/10.30686/1609-9192-2023-1-39-44

2. Акматов Д.Ж., Тихонов А.А. Каппушев Д.З. Численное моделирование геомеханических процессов при строительстве перегонных тоннелей Московского метрополитена. Горная промышленность. 2022;(1):133–137. https://doi.org/10.30686/1609-9192-2022-1-133-137

3. Быстрова И.В., Смирнова Т.С. Геологическое моделирование усовершенствования процессов поиска, разведки, разработки залежей. Геология, география и глобальная энергия. 2020;(3):9–16. Режим доступа: https://geo.asu.edu.ru/files/3(78)/9-16.pdf

4. Сухинов А.И., Проценко С.В., Проценко Е.А. Численное моделирование трехмерных турбулентных течений на основе математической модели волновых процессов. Вычислительная механика сплошных сред. 2023;16(2):159–170. https://doi.org/10.7242/1999-6691/2023.16.2.13

5. Головченко Ю.Ю., Лепехин И.С., Румянцев А.Е., Соннов М.А., Трофимов А.В. Разработка численных геомеханических моделей с различной степенью детализации на примере шахты «Ангидрит» рудника «Кайерканский». Горная промышленность. 2023;(4):79–88. https://doi.org/10.30686/1609-9192-2023-4-79-88

6. Акматов Д.Ж., Маневич А.И., Татаринов В.Н., Шевчук Р.В., Морозов О.А. Трёхмерная структурно-тектоническая модель участка «Енисейский» (Нижнеканский массив). Горный журнал. 2023;(1):69–74. https://doi.org/10.17580/gzh.2023.01.11

7. Морозов В.Н., Маневич А.И., Татаринов В.Н. Ретроспективный прогноз места и интенсивности двух сильных коровых землетрясений в Иране и Индии. Вулканология и сейсмология. 2023;(3):69–78. https://doi.org/10.31857/S020303062370013X

8. Шевчук Р.В., Маневич А.И., Акматов Д.Ж., Урманов Д.И., Шакиров А.И. Современные методы, методики и технические средства мониторинга движений земной коры. Горная промышленность. 2022;(5):99–104. https://doi.org/10.30686/1609-9192-2022-5-99-104

9. Гвишиани А.Д., Татаринов В.Н., Кафтан В.И., Маневич А.И., Минаев В.А., Устинов С.А., Шевчук Р.В. Геодинамическая модель северной части Нижнеканского массива: разломная тектоника, деформации, изоляционные свойства пород. Доклады Российской академии наук. Науки о Земле. 2022;507(1):67–74. https://doi.org/10.31857/S2686739722601399

10. Морозов В.Н., Маневич А.И. Механизм формирования разрыва землетрясения Хансин-Авадзи (г. Кобе, Япония) 17.01.1995 М 6.9. Доклады Российской академии наук. Науки о Земле. 2021;499(2):151–158. https://doi.org/10.31857/S2686739721080089

11. Gvishiani A.D., Tatarinov V.N., Manevich A.I., Kaftan V.I. Geodynamic interpretation of modern movements in the southern part of the Yenisei Ridge (in application to the problems of underground isolation of radioactive waste). Eurasian Mining. 2021;(2):7–11. https://doi.org/10.17580/em.2021.02.0