Уточнение методов расчета грузопотоков конвейерных транспортных систем угольных шахт

О.А. Агафонов¹, Н.Б. Афонина^2
1 ООО «Южная угольная компания», г. Москва, Российская Федерация
² Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова, г. Новочеркасск, Российская Федерация
Горная Промышленность №6 / 2023 стр. 89-94

Резюме: Производительность горного предприятия ограничивается возможностью транспортной подсистемы, повышение эффективности которой является актуальной научно-практической задачей. Изучение процессов формирования и преобразования грузопотоков позволяет уточнить методику проектирования систем непрерывного транспорта. Нормативная методика выбора ленточных конвейеров базируется на представлении о грузопотоках как о нормально распределенных случайных величинах, при этом в качестве основного показателя используется точечная величина – коэффициент неравномерности. Возникают сомнения в методической оправданности такого подхода. Нормальный закон распределения в классическом варианте адекватно описывает случайную величину, изменяющуюся в бесконечных пределах, а реальные шахтные грузопотоки конвейерных линий представляют собой случайные величины с двусторонними ограничениями. Большинство задач по установлению расчетных диапазонов грузопотоков может быть решено на основе использования опытно установленных функций распределения (или плотности вероятностей) случайных величин грузопотоков. Опираясь на публикации последних лет, а также на собственные экспериментальные исследования, предлагаем описывать грузопотоки кусочно-линейными функциями плотности вероятностей, в частности треугольными, а суммирование грузопотоков производить на основе общих теоретических положений классической теории вероятностей. В статье решена частная задача нахождения аналитического решения суммы двух случайных грузопотоков, заданных треугольными законами распределения, выполнено сравнение результатов численного интегрирования плотностей вероятностей грузопотоков.

Ключевые слова: шахтный грузопоток, методы прогнозирования, ленточный конвейер, плотность распределения грузопотока, функция распределения грузопотока, суммирование случайных грузопотоков

Для цитирования: Агафонов О.А., Афонина Н.Б. Уточнение методов расчета грузопотоков конвейерных транспортных систем угольных шахт. Горная промышленность. 2023;(6):89–94. https://doi.org/10.30686/1609-9192-2023-6-89-94

Информация о статье

Поступила в редакцию: 21.09.2023

Поступила после рецензирования: 24.10.2023

Принята к публикации: 24.10.2023

Информация об авторах

Агафонов Олег Анатольевич – технический директор, ООО «Южная угольная компания», г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Афонина Наталия Борисовна – кандидат технических наук, доцент кафедры горного дела, Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова, г. Новочеркасск, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

Удаление горной массы, состоящее из погрузки и транспортирования, – одна из важнейших составляющих технологического процесса горного предприятия, ведущего добычу полезных ископаемых подземным способом, или при строительстве подземных сооружений. Для построения высокоэффективных конвейерных систем необходимы научно обоснованные методы решения частных задач, описывающих формирование и технологическую трансформацию случайных грузопотоков:

– описание статистических закономерностей возникновения и развития грузопотоков в первичных звеньях – в очистных и подготовительных забоях;

– распределение грузопотока по протяжённости конвейерной установки и расчёт его вероятностных характеристик;

– суммирование грузопотоков с известными вероятностными характеристиками и получение результирующих показателей на выходе;

– трансформация вероятностных характеристик грузопотока при прохождении через аккумулирующую ёмкость.

Транспортные системы современных шахт часто имеют высокую разветвленность, протяжённость и работают с высокой нагрузкой. При этом надёжность конвейерной системы как системы с последовательно включёнными элементами чрезвычайно сильно зависит от надёжности каждого элемента (конвейер, бункер, перегрузочные устройства), которая, в свою очередь, определяется правильным учётом и прогнозированием изменения характеристик шахтных грузопотоков.

Теоретическими и экспериментальными исследованиями процессов формирования грузопотоков и вопросами проектирования конвейерных установок занимались многие учёные на протяжении последних десятилетий. Установлено, что забойные грузопотоки являются случайными несимметричными функциями времени и существенно отличаются от нормального закона распределения. При расчёте возможной нагрузки на очистной забой, как правило, принимаются средние значения влияющих факторов. Но в современных длинных и высокопроизводительных лавах близкий к максимальному грузопоток формируется в течение длительного времени. В этом случае выбор принимающего подлавного конвейера по стандартной методике не гарантирует от аварийных перегрузов.

Используемые в настоящее время подходы к проектированию конвейерных транспортных систем [1–5] не в полной мере учитывают изменившиеся условия работы, необходим учёт фактических вероятностных параметров шахтных грузопотоков в современных шахтах.

Анализ существующих методик проектирования шахтных конвейерных систем

Современная теория формирования и преобразования грузопотоков базируется на представлении о том, что исходные случайные грузопотоки за чистое время работы добычных и проходческих машин имеют нормальное распределение. Для таких грузопотоков разработаны методы расчёта при их различных преобразованиях.

Основные задачи оценки величины грузопотоков при их перемещении по объектам конвейерной транспортной системы сводятся к частным вариантам: группировки, разгруппировки потоков, осреднения в период перемещения груза по длине конвейера и в промежуточных ёмкостях. Перечисленные задачи в отраслевой методике [3] решаются путём введения и преобразования коэффициентов неравномерности отдельных грузопотоков. Коэффициент неравномерности грузопотока в течение 1 мин чистого машинного времени определён следующим образом:

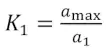, (1)

где a_max – максимальный минутный грузопоток, поступающий на конвейер, т/мин; a₁ – средний минутный грузопоток, поступающий на конвейер, т/мин.

Рассмотрим общие подходы, используемые в отраслевой методике при формировании значения суммарного грузопотока.

При слиянии n грузопотоков, поступающих на сборную транспортную систему, суммарный минутный грузопоток за все время его формирования a_{max Σ} предлагается определять по формуле [5]:

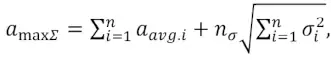(2)

где a_avg.i – средний грузопоток, поступающий из i-й магистрали; n_σ – вероятностный параметр; σ_i – среднее квадратическое отклонение минутного грузопотока за время поступления из каждого забоя, подающего груз на сборный конвейер.

Значение n_σ рекомендовано принимать в функции числа забоев, подающих груз на сборную выработку. Для n ϵ [2–4]:

(3)

Значение σ для каждого входного грузопотока рекомендуется рассчитывать по формуле:

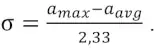(4)

Рассматриваемая методика приводится в исходных документах по проектированию конвейерных транспортных систем [3] без ссылок на источники формирования этой информации. Судя по использованию в отраслевой методике параметров распределения a_avg и σ, за основу принимается нормальное распределение случайных величин входящих грузопотоков. В соответствии со свойствами нормального распределения максимальное значение случайной величины amax определяется «правилом трёх сигм», т.е. может быть вычислено по (2) при значении n_σ = 3. При этом вероятность достижения такого значения составляет около 0,001. Что же касается принятого в отраслевой методике значения n_σ =2,1, то вероятность его реализации составит около 0,013. В доступной литературе отсутствует доказательная база выбора значения nσ. Другим ограничением, введённым без должных обоснований, является расчётное значение среднего квадратического отклонения для каждого из суммируемых потоков, вычисляемое по (4).

Введённая в расчёт величина квантиля нормального распределения n_σ = 2,33 также не имеет обоснования. Частным случаем рассматриваемой методики является слияние n одинаковых потоков, имеющих одинаковую среднюю производительность и одинаковую неравномерность k₀. Неравномерность k_Σ суммарного потока при измерении его в том же мерном интервале будет равна:

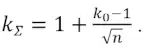(5)

Таким образом, согласно существующим представлениям, положенным в основу современной теории выбора параметров конвейерных установок, чем больше потоков объединяется, тем меньше неравномерность суммарного потока.

Выбор конвейерной установки для конкретных условий эксплуатации согласно существующей методике производится в два этапа: на первом этапе по максимальному грузопотоку выбираются ширина конвейерной ленты и скорость ее движения, т.е. приёмная способность конвейерной установки; а на втором этапе – по расчётному грузопотоку определяется максимально допустимая длина конвейерной установки.

Расчётный грузопоток, т/ч, определяется следующим образом:

(6)

где K_L – коэффициент неравномерности грузопотока за время прохождения груза по всей длине конвейера:

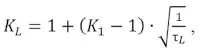(7)

где τ_L – время прохождения груза по всей длине конвейера, мин:

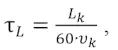(8)

где L_k – длина конвейерной установки, м; υ_k – скорость движения конвейерной ленты, м/с.

С учетом (7) и (8),

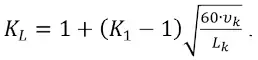(9)

Таким образом, расчётный грузопоток для тягового расчёта конвейерной установки можно определить по формуле:

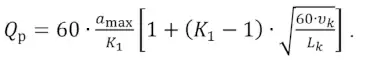(10)

Данная формула имеет неявное ограничение сверху в виде приёмной способности, и если его не учитывать, то возможны варианты, при которых величина расчётной производительности превысит максимально возможный поступающий на конвейер грузопоток (рис. 1), что не имеет физического смысла.

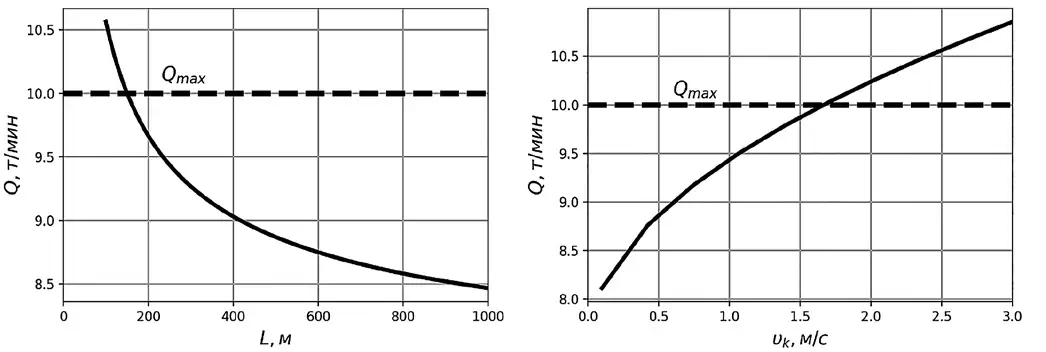Рис. 1 Зависимость эксплуатационной производительности от длины и скорости конвейера (например, Q_max = 10 т/мин; K_n = 1,33; υ_к = 2,5 м/с)

Fig. 1 Dependence of operating capacity on conveyor length and speed (e.g., Q_max = 10 t/min; K_n = 1.33; υ_к = 2.5 m/s)

В последнее десятилетие разными исследователями [6–11] установлено, что важнейшее значение для обоснованного выбора типоразмера конвейера и эксплуатационного проверочного расчёта имеют характеристики грузопотоков с вероятностными характеристиками, существенно отличающимися от нормального закона распределения.

Возможность обоснованного применения изложенного выше «классического» подхода к описанию современных грузопотоков из энерговооруженных угольных забоев вызывает существенные возражения.

Экспериментальные исследования

С целью получения интегральных характеристик формирования грузопотоков на шахте «Садкинская» были проведены производственные замеры грузопотока из очистного забоя длиной 300 м и вынимаемой мощностью пласта 2,08 м, оснащенного комбайном КДК-500. Методика и результаты данных экспериментов приведены в [12].

В результате проведённых опытов были построены функциональные характеристики грузопотока от комбайна в лаве (рис. 2) и установлено, что закон распределения грузопотоков значительно отличается от нормального. В первом приближении возможна их аппроксимация до треугольного закона распределения [12].

Аналитическое решение плотности суммарного грузопотока

Для получения аналитического решения [13] суммирования шахтных грузопотоков с треугольными функциями распределения был рассмотрен упрощённый вариант: суммирование двух одинаковых случайных величин с плотностями вероятностей, представленными на рис. 2.

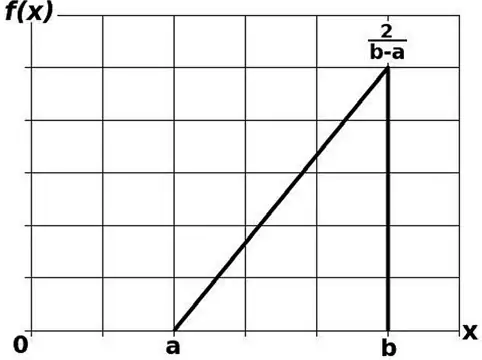Рис. 2 Функция плотности распределения грузопотока треугольной формы

Fig. 2 Density distribution function in the material flow of triangular shape

Плотность вероятностей:

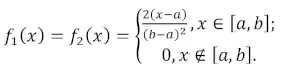(11)

Тогда плотность вероятностей суммы двух «треугольных» грузопотоков можно определить через интеграл свёртки [13; 14]:

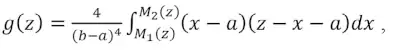(12)

где M₁ (z) и M₂ (z) – область определения подынтегральных функций, за пределами которых функция равна нулю.

Полученное решение [13] не зависит от формы функции плотности распределения и его можно использовать для суммирования двух грузопотоков, описываемых одинаковыми кусочно-линейными функциями (необязательно треугольными). Однако данное решение довольно громоздко и зависит от интервала определения суммарной функции:

– на интервале z ϵ [2a,a + b]:

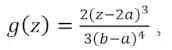(13)

– и на интервале z ϵ [a + b, 2b]:

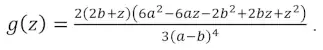(14)

На рис. 3 приведены результаты применения аналитического и численного решения задачи суммирования двух грузопотоков, распределенных по треугольному закону распределения.

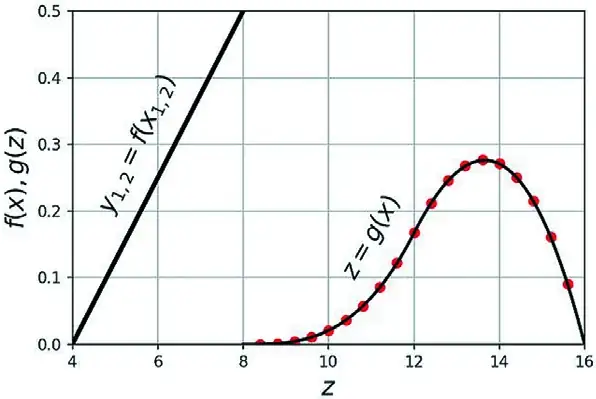Рис. 3 Функция плотности исходных грузопотоков y1,2 и суммарная функция плотности z, точками отмечено численное решение

Fig. 3 The density function of the original material flows y1,2 and the total density function z, the dots indicate the numerical solution

Интересно сравнить дискретные случайные величины, распределенные нормально и по треугольному закону (данные взяты из производственных наблюдений). При одинаковом математическом ожидании в 7,5 т/мин треугольное распределение имеет максимум вероятности грузопотока на большем значении на 8 т/мин. Также отличаются максимальные значения и их вероятности.

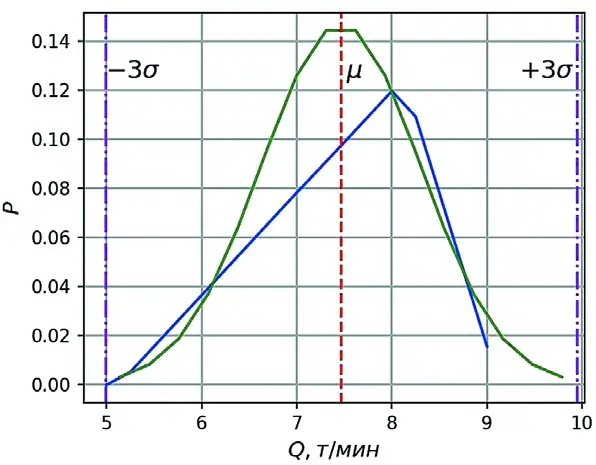Рис. 4 Функции плотности смоделированных «нормального» и «треугольного» грузопотоков

Fig. 4 Density functions of the modeled “normal” and “triangular” material flows

В существующих методиках математическое ожидание в качестве среднего грузопотока используется при определении коэффициента неравномерности. Там же используется максимальный грузопоток. Для реальных грузопотоков более правдоподобным может быть использование наиболее вероятного грузопотока, т.е. моды распределения, что приводит к уменьшению коэффициента неравномерности и предъявляет повышенные требования к пропускной способности проектируемой конвейерной системы (рис. 5).

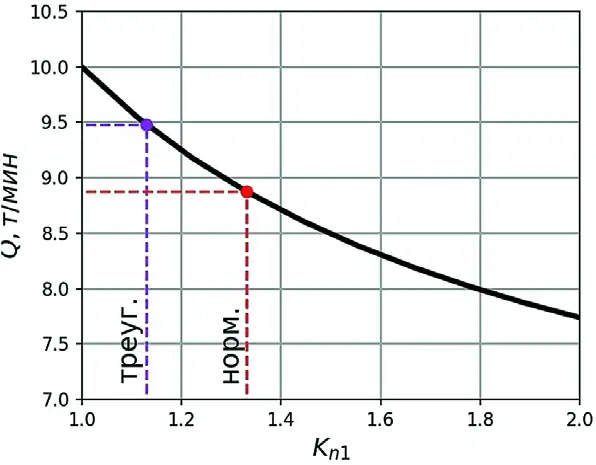Рис. 5 Выбор скорости движения ленты (приемной способности) в зависимости от коэффициента неравномерности при разных законах распределения грузопотоков

Fig. 5 Selection of belt speed (receiving capacity) depending on the nonuniformity coefficient at different laws of the material flow distribution

Численное решение имеет неоспоримое преимущество перед аналитическим в том, что позволяет получать результат суммирования функций, описывающих грузопотоки с любыми законами распределения [14].

Численное имитационное моделирование

Для получения множества решений, описывающих поведение грузопотока с течением времени при транспортировании его по конвейеру, выполнено имитационное численное моделирование с параметрами распределения грузопотока, полученными в производственных замерах. Средняя погонная нагрузка конвейера в течение времени Δt:

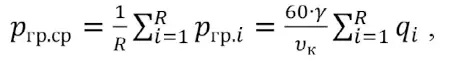(15)

где R – количество порций груза на конвейере:

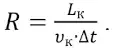(16)

Из результатов моделирования (рис. 6) видно, что средний грузопоток по длине конвейера практически не зависит от длины транспортирования, а определяется только средним значением поступающего грузопотока, что противоречит соотношению (10).

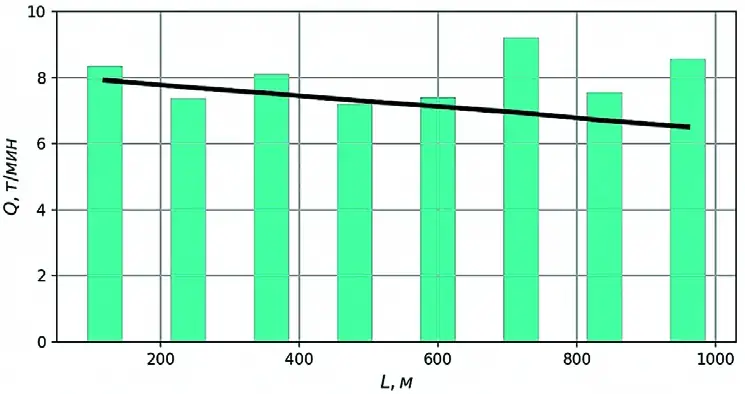Рис. 6 Результат имитационного моделирования загрузки конвейера по длине

Fig. 6 Result of simulation modeling of conveyor loading lengthwise

При этом распределение порций груза на конвейере за период имитационного моделирования существенно отличается от нормального (рис. 7). Действительно, если рассматривать ленточный конвейер с загрузкой в начале и разгрузкой в конце установки, отсутствием промежуточных погрузочно-разгрузочных операций, то порции груза, поступающие на конвейер с задержкой, равной времени транспортирования их до разгрузки, не изменяются (за исключением незначительного естественного осыпания с уменьшением угла откоса).

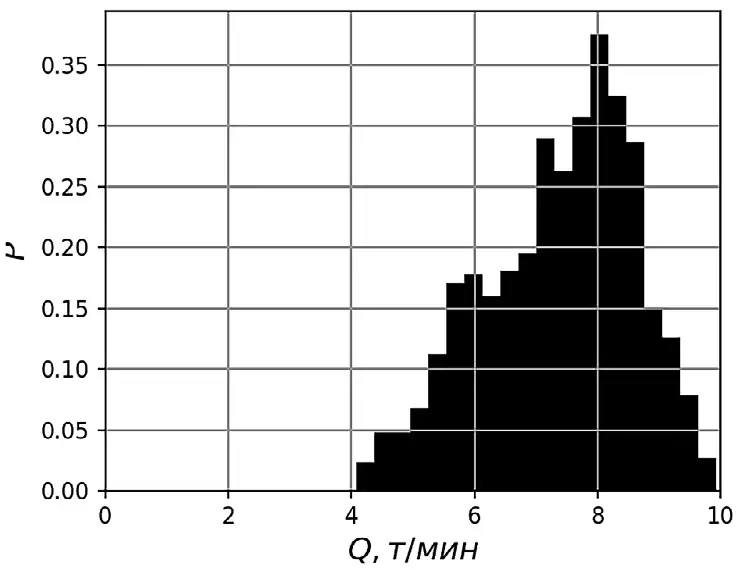Рис. 7 Распределение значений порций груза, поступающего на конвейер по результатам имитационного моделирования

Fig. 7 Value distribution of material portions entering the conveyor based on the simulation modeling results

При этом большую роль играет согласование приемной скорости конвейера и питающего этот конвейер устройства (лавный конвейер, ковш погрузчика и т. д.). Возможны следующие варианты соотношений:

1) υ_к = υ_п – скорости совпадают, грузопоток на выходе конвейера совпадает с грузопотоком на выходе питающего конвейер устройства;

2) υ_к > υ_п – скорость ленты конвейера выше, значит поступающий груз «растягивается» по ленте на любом рассматриваемом отрезке времени, и грузопоток на выходе конвейера уменьшается;

3) υ_к < υ_п – скорость ленты конвейера ниже, значит поступающие новые порции груза в каждый момент времени будут частично суммироваться с порцией груза с предыдущего момента времени, и грузопоток на выходе конвейера возрастает.

Выводы

Применяемые в отраслевой методике проектирования конвейерных транспортных систем положения о нормальном распределении случайных величин грузопотоков и точечном значении максимальных грузопотоков, вычисляемых с использованием коэффициента неравномерности, не имеют достаточных обоснований в известной литературе.

Для решения всей совокупности задач, необходимых для обоснованного выбора конвейеров по их пропускной способности и проверки их тяговых возможностей, необходима достоверно установленная информация о функциях распределения (или плотности вероятностей) исходных грузопотоков, формируемых в очистных и подготовительных забоях; эта информация позволит установить аналогичные функциональные показатели при слиянии потоков, распределении массы груза вдоль става конвейера и при прохождении потока через бункер.

Впервые грузопотоки, формирующиеся в очистных и подготовительных забоях шахты, описаны с помощью кусочно-линейной треугольной функции, что позволяет адекватно отобразить реальные транспортные конвейерные процессы. Такое представление грузопотоков дает возможность с принципиально новых позиций рассмотреть все базовые вопросы выбора и проверочного расчета линейных (одиночных) и сборных конвейеров. Дальнейшие исследования закономерностей формирования случайных грузопотоков конвейерной системы требуют на новой методической основе решения актуальных задач распределения транспортируемого материала по протяженности конвейера и прохождения грузопотока через аккумулирующие емкости.

Список литературы

1. Мерцалов Р.В. Исследования подземных грузопотоков и установление способов повышения эффективности использования шахтных конвейеров: дисс. … канд. техн. наук. М.; 1968. 167 с.

2. Шахмейстер Л.Г., Дмитриев В.Г., Лобачева А.К. Динамика грузопотоков и регулирование скорости ленточного конвейера. М.; 1972. 163 с.

3. Основные положения по проектированию подземного транспорта для новых и действующих угольных шахт. М.: ИГД им. А.А. Скочинского; 1986. 356 с. Режим доступа: https://meganorm.ru/Data2/1/4293726/4293726136.pdf

4. Пейсахович Г.Я. (ред.) Методики расчета и выбора оборудования подземного транспорта угольных шахт на стадии ТЭО. М.: ЦентроГипроШахт; 1980. 47 с. Режим доступа: https://meganorm.ru/Data2/1/4293736/4293736806.pdf

5. Пейсахович Г.Я., Романов И.П. (ред.). Подземный транспорт шахт и рудников. Справочник. М.: Недра; 1985. 565 с.

6. Дьяченко В.П. Влияние параметров случайного грузопотока на выбор типоразмера конвейерной ленты. Горный информационно-аналитический бюллетень. 2005;(1):272–274.

7. Дьяченко В.П. Прогнозирование величины случайных забойных грузопотоков угольных шахт. Горный информационно-аналитический бюллетень. 2009;(S16):199–208.

8. Кондрахин В.П., Стадник Н.И, Белицкий П.В. Статистический анализ эксплуатационных параметров шахтного ленточного конвейера. Науковi працi донецького нацiонального технiчного унiверситету. Серiя: Гiрничо-електромеханiчна. 2013;(2):140–150.

9. Semenchenko A., Stadnik M., Belitsky P., Semenchenko D., Stepanenko O. The impact of an uneven loading of a belt conveyor on the loading of drive motors and energy consumption in transportation. Eastern-European Journal of Enterprise Technologies. 2016;4(1):42–51.

10. Реутов А.А. Имитационное моделирование ступенчатого регулирования скорости конвейера. Проблемы недропользования. 2017;(2):26–32. https://doi.org/10.18454/2313-1586.2017.02.026

11. Дмитриева В.В., Сизин П.Е. Корреляционный анализ и методы моделирования случайного грузопотока, поступающего на сборный конвейер. Горный информационно-аналитический бюллетень. 2018;(10):145–155. https://doi.org/10.25018/0236-1493-2018-10-0-145-155

12. Агафонов О.А. Экспериментальные исследования грузопотока в очистном забое ООО «Шахтоуправление «Садкинское». В кн.: Современные прикладные исследования: Материалы третьей национальной науч.-практ. конф., г. Шахты, 16–19 апреля 2019 г. Новочеркасск: Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова; 2019. С. 71–76.

13. Agafonov O.A., Khazanovich G.S., Otrokov A.V. An analytical solution to the problem of summing two freight flows given by triangular distributions. In: 2020 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), October 6–9, 2020. Vladivostok; 2020, pp. 1–5. https://doi.org/10.1109/FarEastCon50210.2020.9271499

14. Агафонов О.А., Отроков А.В. Численное решение проблемы суммирования непрерывных грузопотоков с произвольным распределением. В кн.: Емельянов Н.В., Кетова К.В. (ред.) Научные исследования и инновации: сборник статей 10-й Междунар. науч.-практ. конф., г. Саратов, 27 июля 2021 г. Саратов: НОО «Цифровая наука»; 2021. С. 87–95.