Создание трехмерной геомеханической модели для оценки устойчивости породного массива
Д.Ж. Акматов1,2, Р.В. Шевчук1,2, Е.А. Тухель2, В.В. Николайчук2, Р.Р. Галиева2
1 Геофизический центр Российской академии наук, г. Москва, Российская Федерация
2 Национальный исследовательский технологический университет «МИСИС», г. Москва, Российская Федерация
Горная Промышленность №1 / 2024 стр. 145-148
Резюме: В современных исследованиях распространено использование трехмерных геомеханических моделей для оценки устойчивости горных пород. Создание трехмерной геомеханической модели представляет собой ключевой этап в исследованиях напряженно-деформированного состояния горных пород. В статье представлен теоретический обзор расчета напряженно-деформированного состояния горных пород. Основная цель работы заключается в создании геомеханической численной модели, направленной на описание напряженно-деформированного состояния горных пород. В ходе моделирования напряженно-деформированного состояния определяется распределение компонент тензора напряжений для различных направлений силового воздействия и других граничных условий с целью определения пределов их изменений. Моделирование напряженно-деформированного состояния в трехмерной постановке осуществляется с использованием метода конечных элементов в программном комплексе COMSOL Multiphysics, что является широко распространенным подходом среди исследователей.
Ключевые слова: геомеханическое моделирование, трехмерная модель, напряженно-деформированное состояние, метод конечных элементов, прочность горных пород, устойчивость массива
Благодарности: Работа выполнена в рамках государственного задания Геофизического центра Российской академии наук, утвержденного Минобрнауки России.
Для цитирования: Акматов Д.Ж., Шевчук Р.В., Тухель Е.А., Николайчук В.В., Галиева Р.Р. Создание трехмерной геомеханической модели для оценки устойчивости породного массива. Горная промышленность. 2024;(1):145–148. https://doi.org/10.30686/1609-9192-2024-1-145-148
Информация о статье
Поступила в редакцию: 29.11.2023
Поступила после рецензирования: 26.12.2023
Принята к публикации: 10.01.2024
Информация об авторах
Акматов Дастан Женишбекович – младший научный сотрудник, Геофизический центр Российской академии наук, г. Москва, Российская Федерация; аспирант кафедры геологии и маркшейдерского дела, Горный институт НИТУ МИСИС, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Шевчук Роман Васильевич – младший научный сотрудник, Геофизический центр Российской академии наук, г. Москва, Российская Федерация; аспирант кафедры геологии и маркшейдерского дела, Горный институт НИТУ МИСИС, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Тухель Екатерина Андреевна – кандидат технических наук, доцент кафедры геологии и маркшейдерского дела, Горный институт НИТУ МИСИС, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Николайчук Виктор Вадимович – аспирант кафедры геологии и маркшейдерского дела, Горный институт НИТУ МИСИС, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Галиева Рита Ришатовна – аспирант кафедры энергоэффективных и ресурсосберегающих промышленных технологий, Институт технологий НИТУ МИСИС г. Москва, Российская Федерация; e- mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Введение
Геомеханическое моделирование представляет собой вариационный процесс определения реакции породного массива на внешние природные и техногенные воздействия [1–3] в виде изменения первоначального поля напряжений.
Разработка геомеханических моделей базируется на ряде дисциплин из области наук о Земле, каждая из которых имеет свой предмет исследований, методические подходы к его изучению, способы получения, интерпретации и представления данных и т.д. Геомеханика – это наука о механических состояниях породных массивов и процессах, развивающихся в них вследствие различных естественных и техногенных физических воздействий, включая внедрение в массив самого подземного объекта. Отсюда геомеханическая модель – это упрощенное отражение наиболее существенных признаков, свойств и процессов в породном массиве и оценка его реакции на внешние воздействия.
Она несет информацию о структуре среды, о физикомеханических свойствах пород, НДС оценку устойчивости в виде численных параметров.
Для оценки механического состояния породного массива, в т.ч. в математических моделях, широко используется термин «устойчивость геологической среды», определение которого приводится в работах [4–8]. Устойчивость геологической среды – это неизменность или изменение свойств, процессов и состояния в таких пределах, которые не приведут к опасным деформациям, напряжениям и структурным нарушениям во вмещающем горные выработки породном массиве в заданном интервале времени [4; 5].
Для определения величин и направлений напряжений имеется большое количество методов и их модификаций, со своими свои преимуществами и недостатками. Их можно условно разделить на три группы: геологические, геомеханическое, геофизические.
Современные программно-аппаратные средства позволяют в рамках создаваемой 3D-модели насыщать и объединять огромные информационные массивы разнородных данных, в том числе физико-механических параметров, в результате чего появляется возможность объемного твердотельного моделирования. В универсальных системах проектирования (AutoCAD, SolidWorks и др.) хорошо реализуется ядро геометрической обработки и твердотельного моделирования. Программные комплексы инженерного анализа методом конечных элементов (COMSOL Multiphysics, PLAXIS, CAE Fidesys, Abaqus, RFEM, SigmaGT, ANSYS, NASTRAN и др.) предоставляют достаточно полный функциональный набор для инженерных расчетов, включая моделирование напряженно-деформированного состояния, НДС собственных частот и форм колебаний, механики деформируемого твердого тела, но ограничены в инструментах интерактивного построения или изменения модели.
Методология
Математическое моделирование НДС определяется решением краевой задачи упругости, вязко-упругости, упругопластичности и т.п. В условиях, когда константы, определяющие деформации и прочность горной породы, либо неизвестны, либо заданы приближенно, упругие модели позволяют получить качественную картину распределения полей напряжений с учетом его структурных неоднородностей. Для расчетов применяют точные аналитические методы и приближенные численные методы. Приближенные численные методы расчетов обладают большой универсальностью, кроме того, они могут быть выполнены с любой заданной точностью [9].
Для большого количества разломов и наличия локальных неоднородностей, а также анизотропии свойств оптимальным с точки зрения точности расчетов является метод конечных элементов (МКЭ). По нему имеется весьма обширный список публикаций, где описаны примеры приложения МКЭ для различных задач [9–11].
МКЭ основан на вариационном исчислении и механике деформированного твердого тела. Краевая задача для упругого потенциала пород, находящегося под действием сил гравитации и тектонических сил, рассматривается как функционал Лагранжа. Расчетная область разбивается на большое количество малых элементов, внутри которых потенциал изменяется линейно. Решается система линейных алгебраических уравнений с большим количеством неизвестных – узловых перемещений, после чего вычисляются деформации и из обобщенного закона Гука напряжения в узлах элементов. При этом в качестве исходных данных используются геометрия модели, упругие свойства и плотность пород, кинематические связи и силовые воздействия [9].
Результатом моделирования является пространственное распределение тензора напряжений, деформаций и параметров, характеризующих устойчивость массива. При этом набор (как исходных, так и на выходе) параметров модели может быть достаточно разнообразным в зависимости от наличия исходных данных и поставленной задачи.
Расчет НДС проводился с МКЭ в трёхмерной постановке:
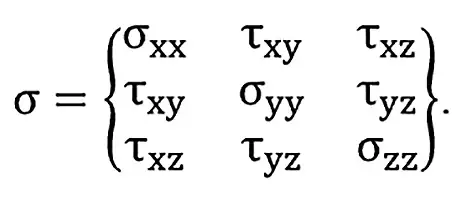
Напряжение бокового отпора принимается по А.Н. Диннику как:
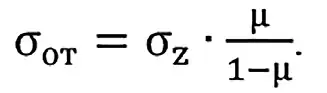
Расчет интенсивности напряжений производился по формуле:
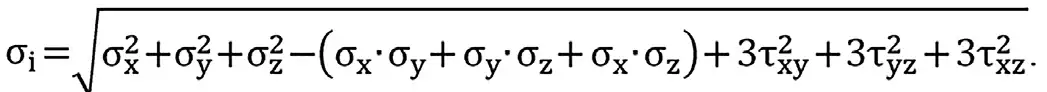
Таблица 1 Исходные данные для трехмерного моделирования
Table 1 Input data for 3D modeling
Результаты
Основной задачей на данном этапе является создание каркасной трехмерной модели (рис. 1, а), включающей литологическую компоненту, разрывные зоны и физико-механические характеристики исследуемого массива [12]. На последующем этапе определяются граничные условия, где вертикальное напряжение соответствует объемному весу горных пород , а горизонтальные напряжения и определяются как произведение коэффициента бокового давления .. на объемный вес и глубину . Модель разбивается на четырехугольные конечные элементы (пирамиды) с использованием метода триангуляции Делоне. Размер конечного элемента постепенно увеличивался к границам каркасной модели, где геометрия модели принимала прямоугольные формы, и ее структура становилась более однородной. Общий вид конечно-элементной модели, наложенной на каркасную модель, представлен на рис. 1, б.
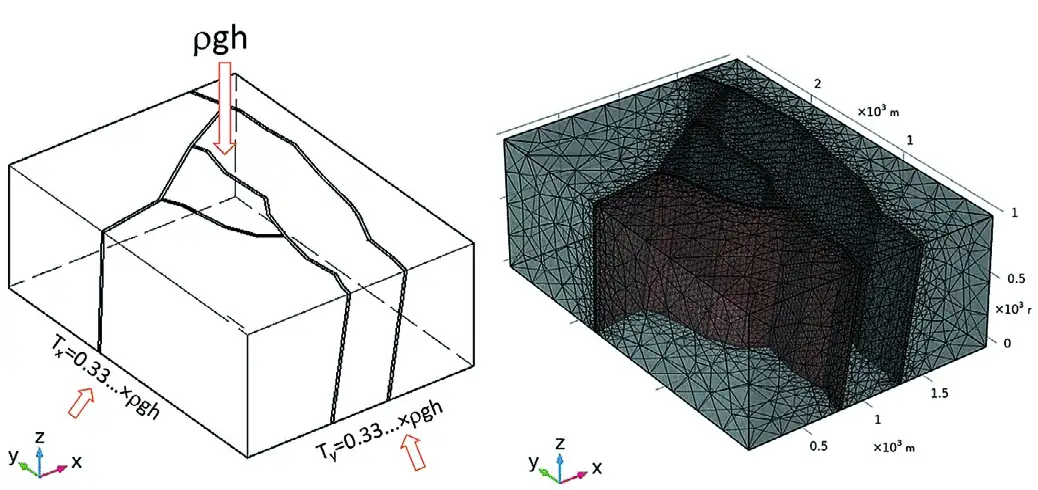Рис. 1 Расчетно-геологическая модель: а – трёхмерная структурная модель; б – трехмерная конечно- элементная модель
Fig. 1 A computational geological model: а – a 3D structural model; б – a 3D finite element model
На рис. 2 приведен расчет интенсивности напряжений . В реальных условиях поле тектонических напряжений существенно осложняет приведенную картину распределения напряжений. Нами было показано, что наличие тектонических разломов в массиве под действием тектонических напряжений приводит к локальной концентрации напряжений, создающей области высоких градиентов тектонических напряжений [13–16]. Учет этих факторов должен быть включен в прогнозирование и оценку устойчивости породного массива.
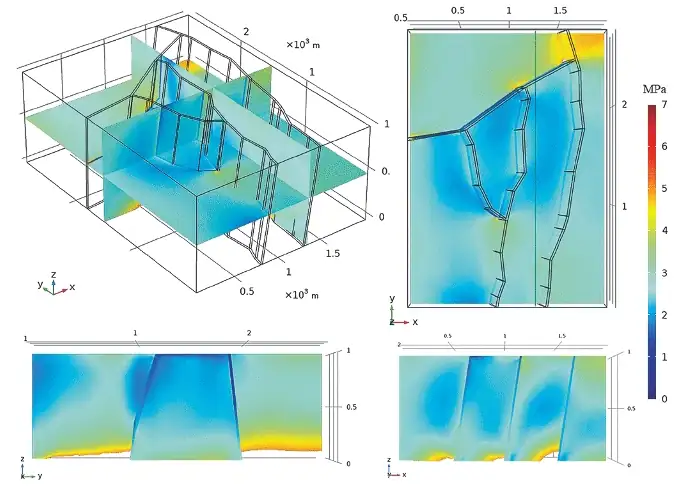Рис. 2 Пример модели интенсивности напряжений σi
Fig. 2 Example of the stress intensity model σi
Выводы
Из результатов анализа опыта проведения геомеханических исследований и построения моделей для оценки устойчивости породных массивов можно сделать следующие выводы:
1. Геомеханические исследования играют принципиально важную роль в обеспечении безопасности при эксплуатации подземного сооружения. Современная концепция геомеханических исследований включает в себя следующие компоненты:
– выбор контролируемых параметров;
– разработку математических моделей НДС;
– оценку и прогноз устойчивости породного массива.
2. Необходимым условием решения этой задачи является обеспечение максимальной достоверности оценки напряженно-деформированного состояния породного массива, которая может быть повышена: а) путем учета влияния структурных элементов породного массива; б) использования геомеханических 3D-моделей.
Существующие методические подходы и современные программно-аппаратные средства создания 3D-моделей позволяют объединять огромные массивы разнородных данных, в том числе физико-механических параметров, в результате чего появляется возможность трехмерного моделирования распределения полей напряжений и параметров, характеризующих устойчивость пород. Программный комплекс инженерного анализа методом конечных элементов (COMSOL Multiphysics) предоставляет достаточно полный функциональный набор для инженерных расчетов.
Список литературы
1. Ляпин И.Н., Королев Д.О., Коровин И.Ю., Корнев А.Ю., Коваль М.Е., Попов А.А. Опыт применения геомеханического моделирования на этапе проектирования скважин. Нефть. Газ. Новации. 2019;(10):17–20.
2. Павлов В.А., Поляков Д.А., Субботин М.Д., Меликов Р.Ф., Павлюков Н.А., Поспелова Т.А. К вопросу импортозамещения в геомеханическом моделировании. Технологии нефти и газа. 2019;(2):3–9.
3. Хлопцова М.В. Задачи геомеханического моделирования при разработке месторождений и эксплуатаций. Горный информационно-аналитический бюллетень. 2017;(4):107–116. Режим доступа: https://giab-online.ru/files/Data/2017/4/107_116_4_2017.pdf (дата обращения: 09.01.2024).
4. Гвишиани А.Д., Кафтан В.И., Красноперов Р.И., Татаринов В.Н. Геоинформатика и системный анализ в геофизике и геодинамике. Физика Земли. 2019;(1):42–60. https://doi.org/10.31857/S0002-33372019142-60
5. Гвишиани А.Д., Татаринов В.Н., Кафтан В.И., Лосев И.О., Маневич А.И. ГИС-ориентированная база данных для системного анализа и прогноза геодинамической устойчивости Нижне-Канского массива. Исследования Земли из космоса. 2021;(1):53– 66. https://doi.org/10.31857/S020596142101005X
6. Морозов В.Н., Маневич А. И., Татаринов В.Н. Моделирование напряженно-деформированного состояния и геодинамическое районирование в сейсмически активных районах. Горный информационно-аналитический бюллетень. 2018;(8):123– 132. https://doi.org/10.25018/0236-1493-2018-8-0-123-132
7. Manevich A.I., Kolikov K.S., Egorova E.A., Geoecological aspects of stress-strain state modeling results of Leninsky coal deposit (Kuzbass, Russia). Russian Journal of Earth Science. 2019;(19):ES4002. https://doi.org/10.2205/2019ES000663
8. Коваленко А.А., Захаров Н.Е., Пул Е.К., Золотин В.Г. Геомеханические аспекты разработки кимберлитового месторождения трубки «Интернациональная». Горный журнал. 2019;(2):27–31. https://doi.org/10.17580/gzh.2019.02.05
9. Морозов В.Н., Татаринов В.Н., Колесников И.Ю., Маневич А.И. Моделирование напряженно-деформированного состояния эпицентральной зоны сильного землетрясения в Иране (26 декабря 2003 г. Mw = 6.6). Физика Земли. 2018;(4):68–78. https://doi.org/10.1134/S0002333718040087
10. Акматов Д.Ж., Евлоев Х.Ю., Меллер А.Д., Манукян Т.А., Чадин В.Н. Методика численного моделирования полей напряжений в районе размещения угольных шахт. Горная промышленность. 2023;(1):39–44. https://doi.org/10.30686/1609-9192-2023-1-39-44
11. Акматов Д.Ж., Кулешов А.М., Чадин В.Н. Богачук А.Г., Колесников К.А. Анализ напряженно-деформированного состояния моделей разрывных нарушений. Горная промышленность. 2023;(5):119–123. https://doi.org/10.30686/1609-9192-2023-5-119-123
12. Акматов Д.Ж., Маневич А.И., Татаринов В.Н., Шевчук Р.В., Морозов О.А. Трёхмерная структурно-тектоническая модель участка «Енисейский» (Нижнеканский массив). Горный журнал. 2023;(1):69–74. https://doi.org/10.17580/gzh.2023.01.11
13. Manevich A.I., Tatarinov V.N., Kolikov K.S. Detection of crustal deformation anomalies with regard to spatial scale effect. Eurasian Mining. 2019;(2):19–22. https://doi.org/10.17580/em.2019.02.04
14. Тарасов Б.Г. Веерный механизм динамических трещин сдвига как источник парадоксов прочности и хрупкости горных пород. Горный журнал. 2020;(1):18–23. https://doi.org/10.17580/gzh.2020.01.03
15. Бирючев И.В., Макаров А.Б., Усов А.А. Геомеханическая модель рудника. Часть 1. Создание. Горный журнал. 2020;(1):42–48. https://doi.org/10.17580/gzh.2020.01.08
16. Съедина С.А., Балтиева А.А., Шамганова Л.С. Разработка 3D геомеханических моделей для подземных рудников и карьеров. Проблемы недропользования. 2018;(1):60–65. https://doi.org/10.25635/2313-1586.2018.01.060
