Численное моделирование процесса копания ковшом экскаватора методом дискретных элементов
В.А. Плащинский, Е.И. Шешукова, А.Э. Салимов, Д.А. Шибанов, С.Л. Иванов
Санкт-Петербургский горный университет императрицы Екатерины II, г. Санкт-Петербург, Российская Федерация
Горная Промышленность №4 / 2025 стр. 144-150
Резюме: В работе исследуется процесс экскавации породы ковшом экскаватора. Проведены численные моделирования процесса копания с варьируемой величиной стружки, крупности и насыпной плотности породы с целью установления данных параметров на усилие при копании и на мощность. В результате численных экспериментов подтверждена адекватность и точность численной модели по критерию соответствия с физической моделью величин усилия копания и массы зачерпнутой породы. Определены функциональные зависимости для вычисления величины усилия копания и мощности в зависимости от данных параметров. Установлено, что, основываясь на энергетическом подходе, можно в зависимости от интенсивности расходования ресурса изменять межремонтный период, мероприятия технического обслуживания и ремонта для горной машины. Численное моделирование рабочих процессов, происходящих в данных машинах, является эффективным инструментом, позволяющим с высокой точностью оценивать вклад различных факторов в интенсивность расходования их ресурса.
Ключевые слова: карьерный экскаватор, DEM, численное моделирование, параметры взаимодействия материалов, сыпучая среда
Для цитирования: Плащинский В.А., Шешукова Е.И., Салимов А.Э., Шибанов Д.А., Иванов С.Л. Численное моделирование процесса копания ковшом экскаватора методом дискретных элементов. Горная промышленность. 2025;(4):144–150. https://doi.org/10.30686/1609-9192-2025-4-144-150
Информация о статье
Поступила в редакцию: 17.05.2025
Поступила после рецензирования: 18.06.2025
Принята к публикации: 20.06.2025
Информация об авторах
Плащинский Вячеслав Алексеевич – кандидат технических наук, ассистент кафедры машиностроения, СанктПетербургский горный университет императрицы Екатерины II, г. Санкт-Петербург, Российская Федерация; https://orcid.org/0000-0003-0326-4514; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Шешукова Екатерина Игоревна – аспирант кафедры машиностроения, Санкт-Петербургский горный университет императрицы Екатерины II, г. Санкт-Петербург, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Салимов Аббос Эркин угли – аспирант кафедры машиностроения, Санкт-Петербургский горный университет императрицы Екатерины II, г. Санкт-Петербург, Российская Федерация
Шибанов Даниил Александрович – кандидат технических наук, доцент кафедры машиностроения, СанктПетербургский горный университет императрицы Екатерины II, г. Санкт-Петербург, Российская Федерация; https://orcid.org/0000-0002-6203-0219
Иванов Сергей Леонидович – доктор технических наук, профессор кафедры машиностроения, Санкт-Петербургский горный университет императрицы Екатерины II, г. Санкт-Петербург, Российская Федерация; https://orcid.org/0000-0002-7014-2464; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Введение
Машины и оборудование, используемые при проведении горных работ подвержены влиянию деградационных процессов, степень этого влияния определяется нагрузками как на всю машину, так и на конкретные узлы [1–3]. Величина нагрузок зависит от условий эксплуатации. Определив изменение величины нагрузки от конкретного параметра, определяющего это нагружение, можно, используя энергетический подход, оценить вклад исследуемого фактора на интенсивность и величину изменения наработки машины [4–6]. Это позволяет корректировать периодичность работ по техническому обслуживанию и ремонту [7–9]. Произвести оценку этого вклада возможно посредством численного моделирования, например, методом дискретных элементов DEM (Discrete elements method), позволяющим исследовать различные объекты и явления без проведения натурных экспериментов, которые часто являются дорогостоящими и труднореализуемыми [10–12].
В горном деле численные методы компьютерного моделирования нашли свое широкое применение [13–15], например, для проверки разработанных теоретических моделей различных процессов в горном производстве [16–18]. Подобные исследования [19–21] также посвящены установлению влияния рабочих параметров на эффективность функционирования горных машин.
Методология
Следует констатировать, что численное моделирование без привязки к реальным физическим процессам само по себе малоинтересно, поскольку отсутствует база для сравнения и оценки адекватности реалиям. С учетом этого факта авторами предварительно было проведено физическое моделирование процесса копания ковшом экскаватора модельной породы в лабораторных условиях [22].
Применительно к исследованию были определены критерии подобия физической модели: линейный коэффициент kt – 20, масштабный коэффициент объемного веса kr – 4, масштабный коэффициент сцепления kc – 80 и масштабный коэффициент усилия kp – 32000. Модель включала в свой состав ковш экскаватора ЭКГ-18Р, прямолинейный участок траектории движения ковша, гранулометрический состав модельной породы и ее насыпную плотность [23–25].
В результате проведенных шести серий лабораторных экспериментов были установлены максимальные усилия копания Fм на ковше экскаватора, возникающие в процессе экскавации им породы в функции толщины стружки h [22].
Линейная аппроксимация результатов экспериментов, имеющая коэффициент детерминации R² = 0,99, позволяет получить функциональную зависимость изменения величины усилия копания ковшом экскаватора модельной породы для заданной толщины стружки в виде выражения:
Высокий коэффициент детерминации говорит об адекватности описания аппроксимированной функцией реальным процессам.
Таким образом, в качестве базы для сравнения с результатами численного моделирования авторами была взята представленная выше функция (1), для чего в программе Ansys Rocky Dem были сформированы условия воспроизведения описанных выше лабораторных экспериментов.
Продолжительность численного моделирования составила 7,5 с. В качестве элемента для создания сетки конечных элементов геометрической модели ковша экскаватора был выбран тетраэдр с размером стороны 0,01 м. В качестве критерия обеспечения качества сетки руководствовались наличием минимум 10 элементов вдоль ребра и 5 поперек [26–28].
Форма частиц при моделировании принималась сферической с определенным в зависимости от крупности радиусом, при этом соотношение частиц различного диаметра выбиралось для каждой серии численных экспериментов свое по схеме: (d1/(x1) + d2/(x2) + d3/(x3) + d4/(x4)). Здесь d – диаметр сферы, а х – объемное содержание этих частиц в смеси, выраженное в относительных единицах так, чтобы сумма х составляла 100%. На рис. 1, где представлена фасетированная модель процесса, сферы разного диаметра указаны различными цветами.
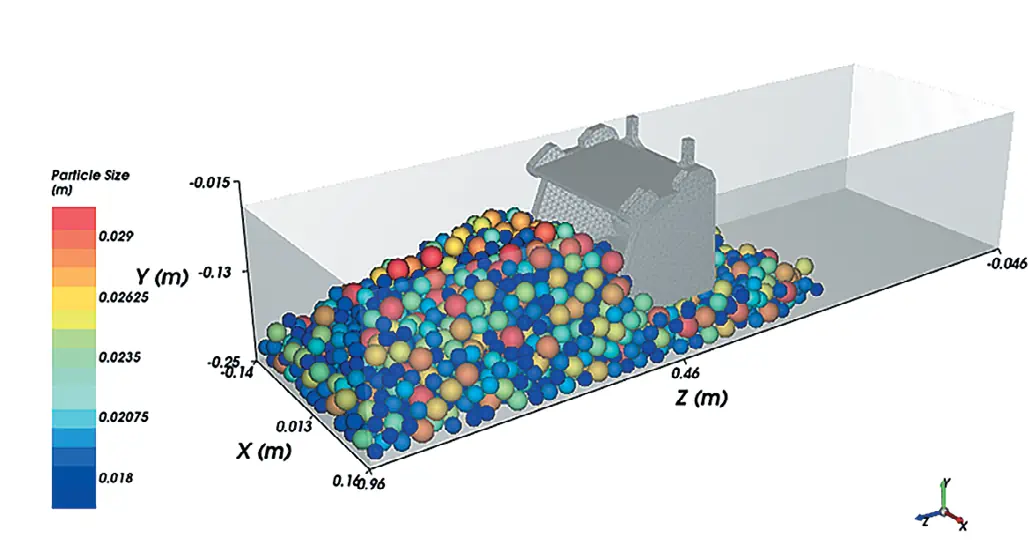Рис. 1 Фасетированная модель процесса копания ковшом модельной породы Для базового варианта при численном моделировании размер преобладающей фракции составил 0,005 м, а соотношение соответствовало схеме: + 0,005(50%) + 0,004(40%) + 0,003(10%). Для расчета контактного взаимодействия сферических частиц в программе была выбрана модель контактных сил – Hertzian spring dashpot и Mindlin Dereciewicz, в качестве модели сопротивления частиц качению – модель Type C [29–31]. Для достижения сходимости результатов численного моделирования и физической модели определены лабораторно и заданы программно параметры взаимодействия контактных пар: коэффициент статического трения – для контактной пары «частицы – ковш экскаватора» – 0,44; «частицы – частицы» – 0,36; коэффициент восстановления – 0,40 и 0,55 соответственно, коэффициент сопротивления частиц качению – 0,4 [32–34].
Для обеспечения адекватности цифровой модели реальным условиям физического моделирования были выбраны два критерия: соответствие усилий на ковше при копании Ftwl и величины массы m зачерпнутого в ковш материала при каждой величине снимаемой стружки h: 0,007 м; 0,014 м; 0,018 м; 0,023 м; 0,032 м; 0,039 м и плотности экскавируемого материала 400 кг/м³ [34; 35]. В процессе численного моделирования собиралась статистика взаимодействия частиц породы с моделью ковша экскаватора, для чего был активирован модуль сбора статистики столкновений «Boundary Collision Statistics». Количество взаимодействующих между собой элементов в численном эксперименте составляет 2,5∙10⁵ сфер, продолжительность одного расчета – 48 ч, где определялись средние нормальные и тангенциальные нагрузки, на основании которых получены полные усилия Fsw.
Полученные в результате численного моделирования усредненные значения усилия копания и массы зачерпнутого ковшом материала имеют хорошее совпадение в пределах от 2 до 8%, что говорит о достаточной адекватности численного моделирования реальным процессам. Тогда правомочно считать, что Fuu = Fu.
Результаты численного моделирования
Получив таким образом мощный инструмент исследования, целесообразно применить его для случаев, когда физический эксперимент провести практически не представляется возможным, а именно оценить раздельно влияние насыпной плотности и гранулометрического состава на величину копания ковшом экскаватора.
Для установления влияния насыпной плотности на усилие при прочих равных условиях на основе созданной модели был проведен численный эксперимент, в рамках которого программно дискретно изменялась плотность породы в сравнении с базовой величиной: 340 кг/м³ (–15%), 428 кг/м³ (+7%), на 460 кг/м³ (+15%), 520 кг/м³ (+30%).
Результаты численного эксперимента представлены на рис. 2.
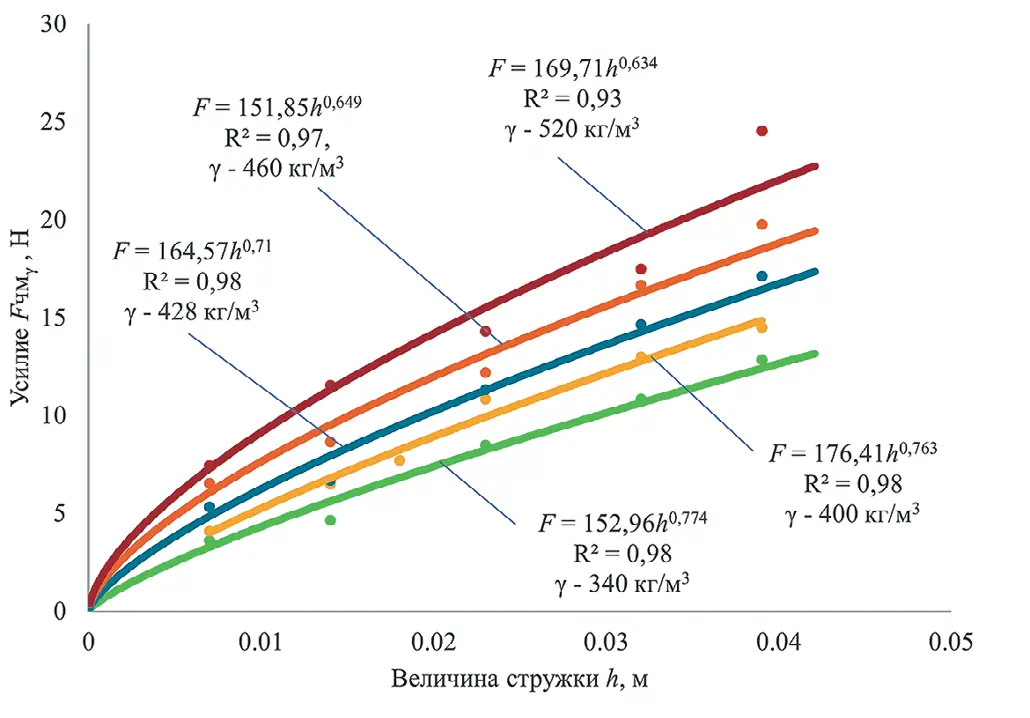Рис. 2 Изменение величины усилия копания Fчмγ от величины стружки h при заданной насыпной плотностиДля выявления универсальной закономерности изменения усилия копания от величины стружки при различных значениях насыпной плотности аппроксимируем полученные точки численного моделирования при одинаковых значениях стружки выражением вида f (F) = Af rp. В результате проведенных преобразований получим функцию изменения величины усилия копания от значений плотности vu породы и величины стружки h:
Приводя выражение к относительному виду и относя эту функцию к функциональной зависимости для базового варианта, получим функцию изменения усилия копания от плотности экскавирусного материала:
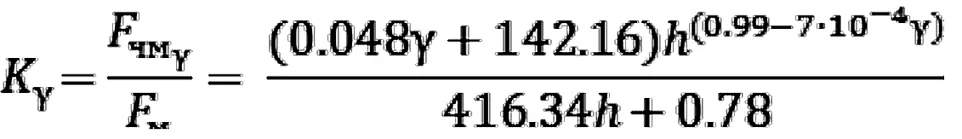(2)Аналогичные численные эксперименты были проведены применительно к различной крупности экскавирусного материала с неизменной плотностью смеси (рис. 3).
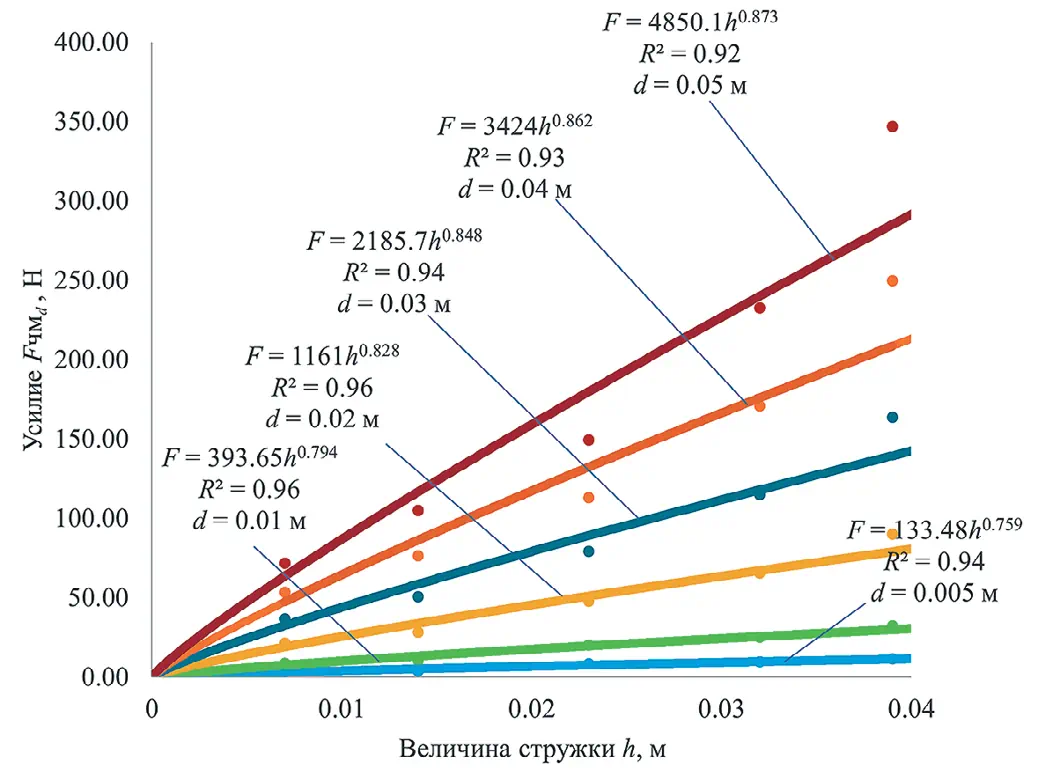Рис. 3 Изменение величины усилия копания Fчмd от величины стружки h при заданной крупности Получим функцию изменения величины усилия копания от значений крупности d породы и величины стружки h:
Fчм d = 519,7*103d1.56h1.06d0.065
Приводя выражение к относительному виду и относя эту функцию к функциональной зависимости для базового варианта, получим функцию изменения усилия копания от крупности экскавирусного материала:
(3)Теперь, базируясь на выражениях (1), (2) и (3), усилие копания ковшом экскаватора применительно к реальным условиям эксплуатации, но с измененной насыпной плотностью и размером куска при известной базовой функциональной зависимости Fuu можно оценить, воспользовавшись выражением:
(4)Для проверки адекватности полученных результатов реально протекающим процессам был поставлен дополнительный физический эксперимент для материала типа керамзит с насыпной плотностью 275 кг/м³ и крупностью 0,005–0,01 м при величине снимаемой стружки 0,034 м. Усилие копания при скорости движения ковша 0,5 м/с составило 12,06 Н, для этих же условий усилие, полученное по выражению (4) при KF = 1 (условие лабораторного эксперимента), составило 13 Н, что подтверждает правильность принятых решений и возможность применения представленного подхода.
На основании представленных выше функциональных зависимостей были получены усилия копания ковшом экскаватора различных насыпной плотности и гранулометрического состава модельной породы, которые представлены в виде 3D-графиков на рис. 4.
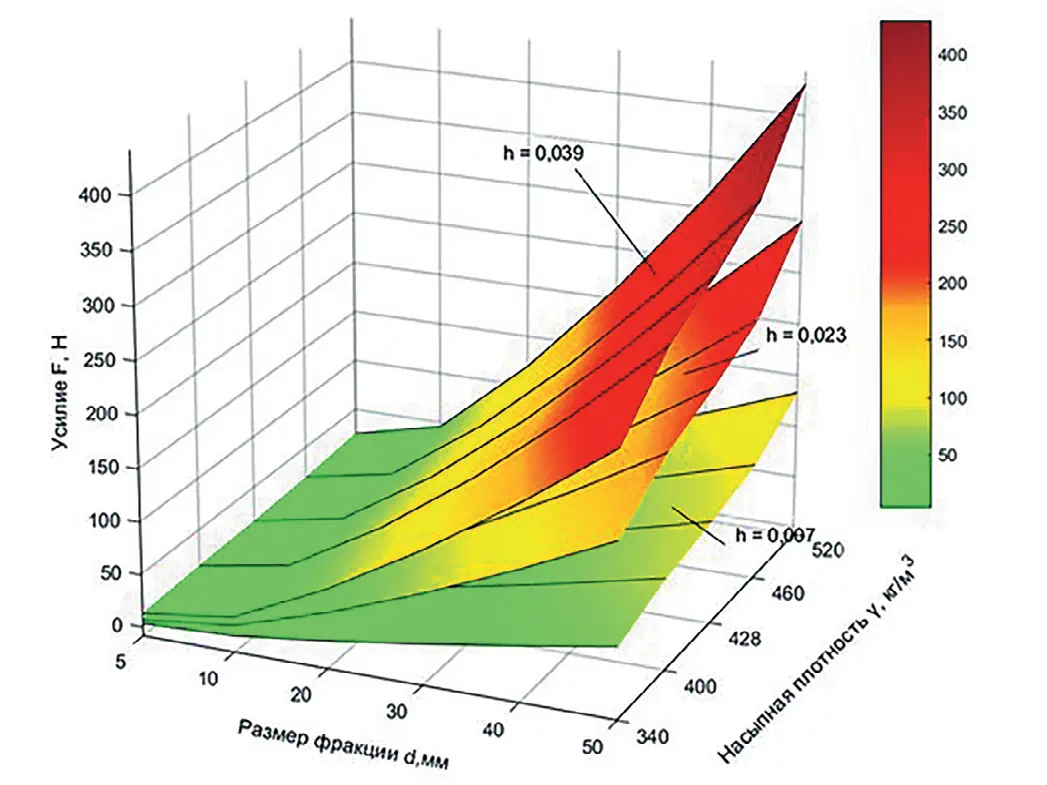Рис. 4 Изменение величины усилия копания Fчм от насыпной плотности и крупности при заданной величине стружки h
Как видно из графика, наиболее резкое увеличение усилия копания наблюдается для стружки 0,039 м при увеличении насыпной плотности и размера фракции, например, усилие копания для стружки 0,039 м при размере 0,05 м и насыпной плотности 520 кг/м³ в среднем 3,5 раза выше в сравнении со стружкой 0,007 м.
Обсуждение результатов
На основании собранной в результате моделирования статистики усилий и перемещений частиц при копании были определены зависимости изменения мощности для рассматриваемых случаев. Так, функция затрат мощности от диаметра куска в цикле копания представлена выражением (5) с коэффициентом детерминации R² = 0,87:
(5)Что касается влияния на энергоемкость процесса копания насыпной плотности, то формула примет вид с коэффициентом детерминации R² = 0,85:
(6)Согласно полученным результатам можно сделать вывод, что при увеличении крупности от 0,005 м значение работы, потребной для преодоления сил сопротивления при копании, возрастает в сравнении с базовой крупностью d = 0,005 м в 10 (1,67d) и 30 (3,75d) раз соответственно, что говорит о степенной зависимости влияния размера куска на энергоемкость процесса. Что касается плотности, то потребная работа оказалась меньше для насыпной плотности 340 кг/м³ на 16% в сравнении с базовой 400 кг/м³, однако при увеличении плотности потребная работа также увеличивается на 21 25 и 32% соответственно для плотностей 428,460, 520 кг/м³.
Зная изменение величины мощности в каждый момент времени цикла, можно найти значение работы за цикл для каждого рассматриваемого условия (площадь под графиком). Определив изменение величины работы конца при копании за цикл при рассматриваемых условиях, можно соотнести это значение с величиной работы при базовых условиях эксплуатации. Такое сравнение с опорой на энергетический подход в вопросе оценки расходования ресурса позволяет оценить интенсивность расходования ресурса в исследуемых условиях эксплуатации, откорректировать периодичность работ по техническому обслуживанию и ремонту экскаватора [35].
Заключение
На основании результатов проведенного эксперимента по физическому моделированию процесса копания породы концом экскаватора создана цифровая модель с условиями, соответствующими физическому эксперименту, подтверждена адекватность и точность созданной модели.
Проведена серия вычислительных экспериментов по установлению влияния величины насыпной плотности и крупности на изменение величины усилия копания при разных величинах срезаемой стружки модельной породы. По полученным результатам моделирования построены зависимости величины усилия от вышеуказанных параметров. На основе анализа полученных зависимостей выведена формула для вычисления усилия копания от трех переменных параметров: насыпной плотности и крупности породы, а также величины стружки. С применением данной формулы построен 3D-график зависимости усилия копания при варьировании вышеуказанных переменных для трех заданных величин стружки.
Определены зависимости изменения мощности копания с течением времени моделирования при варьировании насыпной плотности и крупности фракции при заданной величине стружки, на основании чего определена общая функциональная зависимость мощности копания от насыпной плотности, крупности фракции и высоты стружки. Показана возможность изменения межремонтного периода и мероприятий технического обслуживания и ремонта в зависимости от интенсивности расходования ресурса.
Список литературы
1. Мякотных А.А., Иванова П.В., Иванов С.Л. Критерии и технологические требования создания мостовой платформы добычи торфяного сырья для климатически нейтральной геотехнологии. Горная промышленность. 2024;(4):116–120. https://doi.org/10.30686/1609-9192-2024-4-116-120 Myakotnykh A.A., Ivanova P.V., Ivanov S.L. Criteria and technological requirements for creation of a bridge platform to extract peat raw materials for climate-neutral geotechnology. Russian Mining Industry. 2024;(4):116–120. (In Russ.) https://doi.org/10.30686/1609-9192-2024-4-116-120
2. Гаращенко Ж.М., Теремецкая В.А., Габов В.В. Отработка угольных целиков унифицированными выемочными модулями локальными забоями. Горная промышленность. 2024;(5S):151–157. https://doi.org/10.30686/1609-9192-2024-5S-151-157 Garashchenko Zh.M., Teremetskaya V.A., Gabov V.V. Mining of coal pillars using unified excavation modules with local faces. Russian Mining Industry. 2024;(5S):151–157. (In Russ.) https://doi.org/10.30686/1609-9192-2024-5S-151-157
3. Назарычев А.Н., Дяченок Г.В., Сычев Ю.А. Исследование надежности тягового электропривода карьерных самосвалов на основе анализа отказов его функциональных узлов. Записки Горного института. 2023;261:363–373. Режим доступа: https://pmi.spmi.ru/pmi/article/view/16189 (дата обращения: 29.03.2025). Nazarychev A.N., Dyachenok G.V., Sychev Y.A. A reliability study of the traction drive system in haul trucks based on failure analysis of their functional parts. Journal of Mining Institute. 2023;261:363–373. Available at: https://pmi.spmi.ru/pmi/article/view/16189 (accessed: 29.03.2025).
4. Ilic D., Katterfeld A. Simulation of Transfer Chutes. In: McGlinchey D. (ens) Simulations in Bulk Solids Handling: Applications of DEM and Other Methods. Wiley‐VCH GmbH; 2023. Chapter 2, pp. 41–77. https://doi.org/10.1002/9783527835935.ch2
5. Шестаков В.С., Брозовский С.Ю., Давыдов П. В. Исследование нагруженности стрелы экскаватора-драглайна. Горный информационно-аналитический бюллетень. 2024;(1-1):167–178. https://doi.org/10.25018/0236_1493_2024_011_0_167 Shestakov V. S., Brozovskiy S. Yu., Davydov P. V. Excavator boom load study dragline. Mining Informational and Analytical Bulletin. 2024;(1-1):167–178. (In Russ.) https://doi.org/10.25018/0236_1493_2024_011_0_167
6. Комиссаров А.П., Маслеников О.А., Набиуллин Р.Ш., Хорошавин С.А. Оценка степени противодействия двигателей приводов главных механизмов карьерного экскаватора. Горное оборудование и электромеханика. 2022;(6):10–16. https://doi.org/10.26730/1816-4528-2022-6-10-16 Komissarov A.P., Maslennikov O.A., Nabiullin R.S., Khoroshavin S.A. Assessment of the degree of counteraction of the drive motors of the main mechanisms of the quarry excavator. Mining Equipment and Electromechanics. 2022;(6):10–16. (In Russ.) https://doi.org/10.26730/1816-4528-2022-6-10-16
7. Корогодин А.С., Иванов С.Л. Оценка технического состояния опорных подшипников скольжения барабанной мельницы при эксплуатации в составе арктического комплекса горного оборудования. Горная промышленность. 2024;(6):144–151. https://doi.org/10.30686/1609-9192-2024-6-144-151 Korogodin A.S., Ivanov S.L. Assessment of the technical condition of drum mill supporting sliding bearings during operation as part of an arctic mining equipment complex. Russian Mining Industry. 2024;(6):144–151. (In Russ.) https://doi.org/10.30686/1609-9192-2024-6-144-151
8. Ботян Е.Ю., Лавренко С.А., Пушкарев А.Е. Методика уточненного расчета межремонтного периода элементов подвески карьерных автосамосвалов посредством учета горнотехнических условий их эксплуатации. Горная промышленность. 2024;(1):71–76. https://doi.org/10.30686/1609-9192-2024-1-71-76 Botyan E.Y., Lavrenko S.A., Pushkarev A.E. Methodology for refined calculation of mean time to repair of mining dump truck suspension elements with account of mining and technical conditions of their operation. Russian Mining Industry. 2024;(1):71–76. (In Russ.) https://doi.org/10.30686/1609-9192-2024-1-71-76
9. Громыка Д.С., Гоголинский К.В. Рекомендации по внедрению методики оценки текущего состояния коронок зубьев ковшей экскаваторов в систему технического обслуживания и ремонта. Горный информационно-аналитический бюллетень. 2023;(8):94–111. https://doi.org/10.25018/0236_1493_2023_8_0_94 Gromyka D.S., Gogolinskiy K.V. Introduction of evaluation procedure of excavator bucket teeth into maintenance and repair: Promptse. Mining Informational and Analytical Bulletin. 2023;(8):94–111. https://doi.org/10.25018/0236_1493_2023_8_0_94
10. Комиссаров А.П., Шестаков В.С., Набиуллин Р.Ш. Разработка цифровой модели рабочего процесса гидравлического экскаватора. В кн.: Технологическое оборудование для горной и нефтегазовой промышленности: сб. тр. 18-й междунар. науч.-техн. конф. «Чтения памяти В.Р. Кубачека», провед. в рамках Уральской горнопромышленной декады, г. Екатеринбург, 2–3 апр. 2020 г. Екатеринбург: УГГУ; 2020. С. 242–247.
11. Алиева Л., Жуков И.А. Повышение эффективности ударно-поворотного бурения горных пород высокой крепости совершенствованием структуры породоразрушающего безлезвийного инструмента. Устойчивое развитие горных территорий. 2024;16(4):1681–1694. https://doi.org/10.21177/1998-4502-2024-16-4-1681-1694 Alieva L., Zhukov I.A. Upgrading rotary-percussion drilling of high - strength rocks by improving the structure of a rockcrushing blade-free tool. Sustainable Development of Mountain Territories. 2024;16(4):1681–1694. (In Russ.) https://doi.org/10.21177/1998-4502-2024-16-4-1681-1694
12. Pervuhin D.A., Trushnikov V.E., Abramkin S.E., Hloponina V.S., Talanov N.A. Development of methods to improve stability of underground structures operation. International Journal of Engineering. 2025;38(2):472–487. https://doi.org/10.5829/ije.2025.38.02b.20
13. Muratbakeev E., Kozhubaev Yu., Yiming Y., Umar S. Symmetrical modeling of physical properties of flexible structure of silicone materials for control of pneumatic soft actuators. Symmetry. 2024;16(6):750. https://doi.org/10.3390/sym16060750
14. Kozhubaev Yu., Yang R. Simulation of dynamic path planning of symmetrical trajectory of mobile robots based on improved A* and artificial potential field fusion for natural resource exploration. Symmetry. 2024;16(7):801. https://doi.org/10.3390/sym16070801
15. Scheffler O.C., Coetzee C.J. Discrete element modelling of a bulk cohesive material discharging from a conveyor belt onto an impact plate. Minerals. 2023;13(12):1501. https://doi.org/10.3390/min13121501
16. Cleary P.W. Effect of rock shape representation in DEM on flow and energy utilisation in a pilot SAG mill. Computational Particle Mechanics. 2019;6(3):461–477. https://doi.org/10.1007/s40571-019-00226-3
17. Kolahi S., Chegeni M.J., Seifpanahi-Shabani K. Investigation of the effect of industrial ball mill liner type on their comminution mechanism using DEM. International Journal of Mining and Geo-Engineering. 2021;55(2):97–107. https://doi.org/10.22059/IJMGE.2020.289423.594826
18. Жуковский Ю.Л., Королев Н.А., Малькова Я.М. Мониторинг состояния измельчения в барабанных мельницах по результирующему моменту на валу. Записки Горного института. 2022;256:686–700. https://doi.org/10.31897/PMI.2022.91 Zhukovskiy Y.L., Korolev N.A., Malkova Y.M. Monitoring of grinding condition in drum mills based on resulting shaft torque. Journal of Mining Institute. 2022;256:686–700. https://doi.org/10.31897/PMI.2022.91
19. Yin Z., Ma D., Li T. Effect of grinding media grading on liner wear and load behavior in a ball mill by using rocky DEM. Lubricants. 2024;12(10):340. https://doi.org/10.3390/lubricants12100340
20. Beloglazov I., Morenov V., Leusheva E., Gudmestad O.T. Modeling of heavy-oil flow with regard to their rheological properties. Energies. 2021;14(2):359. https://doi.org/10.3390/en14020359
21. Coetzee C.J., Scheffler O.C. Review: The calibration of DEM parameters for the bulk modelling of cohesive materials. Processes. 2023;11(1):5. https://doi.org/10.3390/pr11010005
22. Шешукова Е.И., Плащинский В.А., Салимов А.Э., Шибанов Д.А., Иванов С.Л. Моделирование процесса копания ковшом экскаватора породы при заданной величине стружки. Горный информационно-аналитический бюллетень. 2024;(S21):3–12. Sheshukova E.I., Plaschinsky V.A., Salimov A.E., Shibanov D.A., Ivanov S.L. Simulation of the process of digging with an excavator bucket of rock at a given chip size. Mining Informational and Analytical Bulletin. 2024;(S21):3–12.
23. Шибаева Д.Н., Терещенко С.В., Асанович Д.А., Шумилов П.А. К вопросу о необходимости классификации горной массы, направляемой на сухую магнитную сепарацию. Записки Горного института. 2022;256:603–612. https://doi.org/10.31897/PMI.2022.79 Shibaeva D.N., Tereshchenko S.V., Asanovich D.A., Shumilov P.A. On the need to classify rock mass fed to dry magnetic separation. Journal of Mining Institute. 2022;256:603–612. https://doi.org/10.31897/PMI.2022.79
24. Северцев Н.А., Дарьина А.Н. Применение критериев подобия при ресурсной отработке сложных технических систем и изделий. Надежность и качество сложных систем. 2020;(4):5–14. https://doi.org/10.21685/2307-4205-2020-4-1 Severtsev N.A., Daryina A.N. Application of similarity criteria for resource development of complex technical systems and products. Reliability & Quality of Complex Systems. 2020;(4):5–14. (In Russ.) https://doi.org/10.21685/2307-4205-2020-4-1
25. Дремин А.В., Великанов В.С. К вопросу о гранулометрическом составе взорванных скальных пород. Горная промышленность. 2023;(4):73–78. https://doi.org/10.30686/1609-9192-2023-4-73-78 Dremin A.V., Velikanov V.S. Regarding the particle-size composition of blasted rocks. Russian Mining Industry. 2023;(4):73–78. https://doi.org/10.30686/1609-9192-2023-4-73-78
26. Великанов В.С., Дремин А.В., Чернухин С.А., Ломовцева Н.В. Технологии нейронных сетей в интеллектуальном анализе данных гранулометрического состава взорванных пород. Горная промышленность. 2024;(4):90–94. https://doi.org/10.30686/1609-9192-2024-4-90-94 Velikanov V.S., Dremin A.V., Chernukhin S.A., Lomovtseva N.V. Neural network technologies in mining data on particle size distribution of muck pile rocks. Russian Mining Industry. 2024;(4):90–94. (In Russ.) https://doi.org/10.30686/1609-9192-2024-4-90-94
27. Wang X., Yi J., Zhou Z., Yang C. Optimal speed control for a semi-autogenous mill based on discrete element method. Processes. 2020;8(2):233. https://doi.org/10.3390/pr8020233
28. Lvov V., Chitalov L. Semi-Autogenous Wet Grinding Modeling with CFD-DEM. Minerals. 2021;11(5):485. https://doi.org/10.3390/min11050485
29. Guo J., Roberts A.W., Jones M., Robinson P. Bulk solids flow at the hopper feeder interface with special plane flow configuration. Powder Technology. 2022;403:117372. https://doi.org/10.1016/j.powtec.2022.117372
30. Klishin S., Mikenina O. DEM generation of particle packs in the Aristotelian mechanics. AIP Conference Proceedings. 2021;2448:020011. https://doi.org/10.1063/5.0073421
31. Zhurkina D.S., Klishin S.V., Lavrikov S.V., Leonov M.G. D DEM-based modeling of shear localization and transition of geomedium to unstable deformation. Journal of Mining Science. 2022;58(3):357–365. https://doi.org/10.1134/S1062739122030024
32. Chimwani N., Bwalya M.M. Exploring the end-liner forces using DEM software. Minerals. 2020;10(12):1047. https://doi.org/10.3390/min10121047
33. Carr M.J., Roessler T., Robinson P.W., Otto H., Richter C., Katterfeld A., Wheeler C.A. Calibration procedure of Discrete Element Method (DEM) parameters for wet and sticky bulk materials. Powder Technology. 2023;429:118919. https://doi.org/10.1016/j.powtec.2023.118919
34. Coetzee C., Scheffler O.C. Comparing particle shape representations and contact models for DEM simulation of bulk cohesive behaviour. Computers and Geotechnics. 2023;159:105449. https://doi.org/10.1016/j.compgeo.2023.105449
35. Шешукова Е.И., Шибанов Д.А., Иванов С.Л., Шишкин П.В. Оценка нагрузок приводов рабочего оборудования карьерного экскаватора (часть 2). Горная промышленность. 2024;(4):108–114. https://doi.org/10.30686/1609-9192-2024-4-108-114 Sheshukova E.I., Shibanov D.A., Ivanov S.L., Shishkin P.V. Assessment of loads at the working attachment of a mine shovel (Part 2). Russian Mining Industry. 2024;(4):108–114. (In Russ.) https://doi.org/10.30686/1609-9192-2024-4-108-114
