Экономико-математическое моделирование добывающей отрасли Республики Саха (Якутия): оценка эффективности использования ресурсов
 В.В. Никифорова1, Е.Э. Григорьева1, М.П. Соломонов2
В.В. Никифорова1, Е.Э. Григорьева1, М.П. Соломонов2
1 Научно-исследовательский институт региональной экономики Севера Северо-Восточного федерального университета им. М.К. Аммосова, г. Якутск, Российская Федерация
2 Федеральный исследовательский центр Якутского научного центра Сибирского отделения Российской академии наук, г. Якутск, Российская Федерация
Горная Промышленность №4 / 2025 стр. 134-139
Резюме: Авторами проведено экономико-математическое моделирование влияния добывающей промышленности на социально-экономическое развитие муниципальных районов Республики Саха (Якутия). На основе производственной функции CES с постоянной эластичностью замещения факторов (капитал, труд) проанализированы пять ключевых добывающих районов: Алданский, Ленский, Мирнинский, Нерюнгринский, Оймяконский, которые обеспечивают более 90% объема добычи полезных ископаемых региона. Для анализа использованы данные статистики за 2000–2023 гг., включающие объем отгруженных товаров собственного производства, стоимость основных фондов и среднегодовую численность работников предприятий. Результаты исследования показали: 1 – наибольшую сбалансированность использования ресурсов в Алданском и Ленском районах; 2 – низкое качество модели в Нерюнгринском, что связано с высокой волатильностью угледобычи и дефицитом данных. На макроуровне Республика Саха (Якутия) в целом – модель демонстрирует почти идеальное соответствие, подтверждая ее применимость для стратегического планирования. Разработанная модель может служить инструментом для оптимизации инвестиций, разработки стратегий устойчивого развития и минимизации рисков в территориях присутствия. Ограничения исследования связаны с недостатком муниципальной статистики, что требует интеграции дополнительных социально-экологических параметров в будущих работах. Для дальнейшего исследования потребуется более дифференцированный подход к управлению на локальном уровне для обеспечения сбалансированного роста
Ключевые слова: добывающая промышленность, Республика Саха (Якутия), производственная функция CES, эластичность замещения, муниципальные районы, эффективность ресурсов
Благодарности: Статья написана в рамках проекта государственного задания Минобрнауки РФ «Современные методы математического моделирования и их приложения» (№ FSRG-2023-0025).
Для цитирования: Никифорова В.В., Григорьева Е.Э., Соломонов М.П. Экономико-математическое моделирование добывающей отрасли Республики Саха (Якутия): оценка эффективности использования ресурсов. Горная промышленность. 2025;(4):134–139. https://doi.org/10.30686/1609-9192-2025-4-134-139
Информация о статье
Поступила в редакцию: 03.05.2025
Поступила после рецензирования: 10.06.2025
Принята к публикации: 23.06.2025
Информация об авторах
Никифорова Валентина Васильевна – кандидат экономических наук, ведущий научный сотрудник, Научно-исследовательский институт региональной экономики Севера Северо-Восточного федерального университета им. М.К. Аммосова, г. Якутск, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Григорьева Елена Эдуардовна – кандидат экономических наук, доцент, ведущий научный сотрудник, Научно-исследовательский институт региональной экономики Севера Северо-Восточного федерального университета им. М.К. Аммосова, г. Якутск, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Соломонов Михаил Прокопьевич – кандидат экономических наук, доцент, ведущий научный сотрудник отдела региональных экономических и социальных исследований, Федеральный исследовательский центр Якутского научного центра Сибирского отделения Российской академии наук, г. Якутск, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Введение
В последние годы добывающая промышленность в социально-экономическом развитии Республики Саха (Якутия) играет все большую роль, если в 2010 г. ее доля в валовом региональном продукте (ВРП) занимала 55%, то в 2023 г. – более 80%. Данный показатель связан с освоением крупных нефтегазовых и золоторудных месторождений. Но вместе с тем влияние добывающей промышленности на социально-экономическую систему локальных территорий присутствия недостаточно изучено.
Сложность и неоднородность ключевых элементов социально-экономической системы северного региона предполагают при разработке модели использование множества методов и инструментариев моделирования как общепринятых, так и адаптированных под решаемые задачи для достижения большей вероятности прогнозирования. Основной целью данной статьи является построение многофакторной модели, которая станет одним из прикладных инструментов управления локальной территорией.
Для достижения поставленной цели следует решить ряд действий:
- обзор и анализ существующих инструментариев методов прогнозирования добывающей промышленности;
- выбор адаптированной методики моделирования, пригодной для локальных территорий присутствия добывающей промышленности;
- обоснование применяемых параметров моделирования;
- определение взаимосвязи показателей добывающей промышленности и социально-экономической системы локальных территорий.
Объектом исследования подобраны муниципальные районы региона, на территориях которых сосредоточены основные разрабатываемые месторождения полезных ископаемых.
Материалы и методы
Для моделирования перспектив развития добывающей промышленности и ее влияния на социально-экономическое развитие региона многими исследователями предлагаются различные методические подходы, учитывающие разные факторы, влияющие на результирующий показатель (объем продукции).
Часть исследователей опираются на изучение производственно-экономических систем на основе модификации нелинейной обобщенной макроэкономической модели Роберта Солоу, разработанной еще в 1950-х гг. [1]. Стоит отметить, что данная модель является как бы отправной точкой для всех современных исследований экономического роста [2].
P.A. Жуков, Н.О. Козлова и др. предлагают регрессионные модели для оценки состояния и перспектив развития добывающей отрасли во взаимосвязи с другими подсистемами, что позволяет достичь наилучших экономических, экологических и социальных результатов функционирования. Они считают, что объем добычи полезных ископаемых может быть смоделирован на основе линейной производственной функции, которая имеет высокую степень соответствия фактическим данным. Значимыми факторами признаками модели являются стоимость основных фондов и занятость в отрасли [3; 4].
T.H. Скуфмина и С.В. Баранов в математико-статистическом моделировании динамики производства ВРП северных территорий, в том числе Республики Саха (Якутия), определяют лучшей моделью прогнозирования индекса физического объема ВРП производственную функцию CES (постоянная эластичность замещения – англ. constant elasticity of substitution) [5].
CES – это свойство производственной функции или функции полезности, при котором эластичность пропорции аргументов функции по отношению к пропорции их предельных продуктов остается неизменной при любых значениях аргументов. Другими словами, способность заменить один фактор производства другим (например, труд капиталом) для поддержания одинакового уровня производства остаётся постоянной на разных уровнях производства [6]. Данная модель наиболее полно раскрывает взаимосвязи между факторами производства. В отличие от традиционных подходов она позволяет учитывать нелинейные зависимости и гибкость в замещении ресурсов[сноска1].
Д. Аджемотлу, П. Рестрепо используют CES-функцию для анализа замещения труда и капитала в условиях автоматизации. Показывают, что эластичность замещения между низкоквалифицированным трудом и роботами выше, чем между высококвалифицированным трудом и капиталом [7].
Д. Хемус и М. Олсен, модифицируя CES-модель для изучения влияния искусственного интеллекта на рынок труда, обнаружили, что автоматизация увеличивает разрыв в доходах, если эластичность замещения труда и капитала больше 1 [8].
П. Штифенхофер считает, что интеграция общего искусственного интеллекта в экономическое производство представляет собой трансформационный сдвиг, имеющий глубокие последствия для рынков труда, распределения доходов и технологического роста. Это исследование расширяет производственную функцию CES, включив в нее труд и капитал, управляемые искусственным интеллектом, наряду с традиционными ресурсами, обеспечивая комплексную основу для анализа экономического воздействия искусственного интеллекта [9].
Д.Р. Бакан и Э. Фархи включают CES-агрегирование в модель межотраслевых связей разных стран, объясняя различия в производительности между ними [10].
Многие исследователи основным объектом математического моделирования рассматривают производственный процесс с выявлением значимых факторов воздействия других подсистем на региональную экономическую систему на основе статистически наблюдаемых закономерностей [11–15].
Мы в своих исследованиях экономико-математического моделирования региональной добывающей промышленности применили производственную функцию, которая считается одной из важных в этом направлении. Классический подход к моделированию производственных процессов с помощью данной функции состоит в анализе динамических рядов экономической системы, характеризующих выпуск продукции Y, а также используемые для этого ресурсы (труд L и капитал K) [5]:
Y(t) = F[K(t), L(t)], (1)
где Y – объем продукции; K – стоимость основных фондов; L – численность занятых.
Объектом исследования нами подобраны 5 муниципальных районов, на долю которых в структуре по виду экономической деятельности «Добыча полезных ископаемых» (ВЭД ДПИ) приходится более 90%: Алданский, Ленский, Мирнинский, Нерюнгринский и Оймяконский (рис. 1).
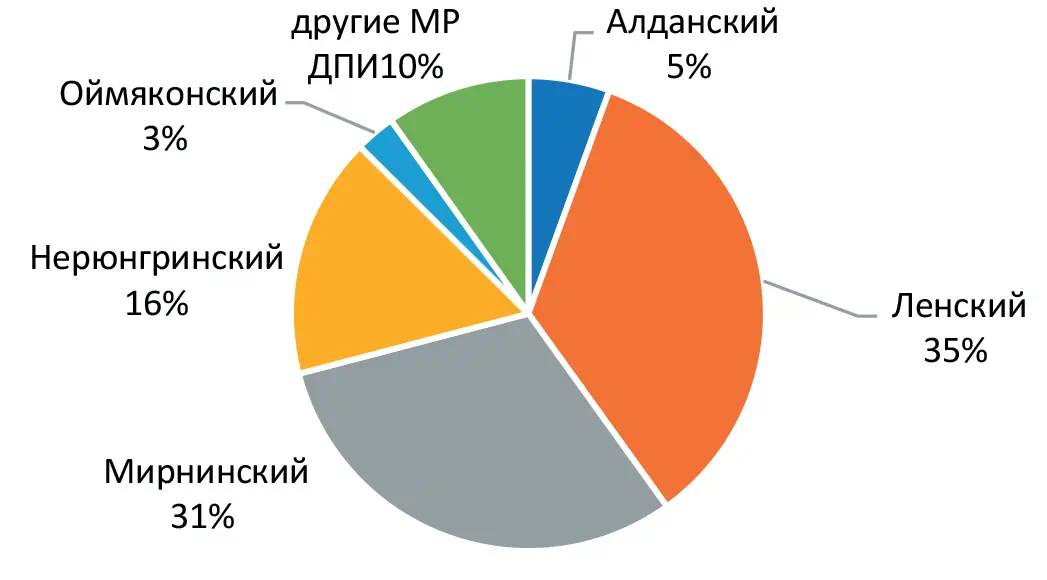
На территориях данных районов ведется добыча высоколиквидных, экспорто-ориентированных видов полезных ископаемых: алмазов, нефти, газа, угля и золота. Недропользователями являются крупные российские компании: «Роснефть», «Газпром», «Полюс», «Сургутнефтегаз», «Колмар» и др.
Прежде чем приступить к моделированию, рассмотрим корреляционную зависимость между оцениваемыми параметрами добывающей промышленности: объемом продукции Y, стоимостью основных фондов K и численностью занятых в отрасли L (табл. 1).
| Муниципальные районы | Y-K | Y-L | K-L |
|---|---|---|---|
| РС(Я) | 0,97 | 0,96 | 0,96 |
| Алданский | 0,76 | 0,90 | 0,82 |
| Ленский | 0,94 | 0,84 | 0,80 |
| Мирнинский | 0,96 | 0,88 | 0,90 |
| Нерюнгринский | 0,50 | 0,89 | 0,53 |
| Оймяконский | 0,89 | 0,80 | 0,74 |
Из данных табл. 1 видно, что наиболее высокие коэффициенты корреляции между оцениваемыми параметрами в целом по республике, а также в Ленском и Мирнинском районах, средние показатели в Оймяконском и в Нерюнгринском районах. Во всех районах наблюдается высокая взаимозависимость между объемом продукции и занятостью населения (0,8–0,96). В целом, можно утверждать, что показатели вполне взаимозависимы.
При моделировании региональной добывающей промышленности применили следующие показатели официальной региональной и муниципальной статистики по Республике Саха (Якутия): объем отгруженных товаров собственного производства, стоимость основных фондов коммерческих и некоммерческих организаций с учетом износа и среднегодовая численность работников организаций (без субъектов малого предпринимательства) муниципальных районов, на территориях которых размещено добывающее производство [сноска2]. Диапазон исследований охватывает 2000–2023 гг. Следует отметить, что на многие показатели муниципальной статистики введены ограничения к открытому доступу. В связи с этим в своих расчетах ограничились доступными статистическими показателями.
К сожалению, целый ряд количественных показателей, которые могут характеризовать добывающую промышленность на практике, не может быть корректно применен на региональном и муниципальном уровне, что усложняет задачу построения прогнозных моделей.
Для моделирования объема отгруженных товаров собственного производства применили производственную функцию CES:
Q = A(αK-ρ + (1-α) L-ρ)-1/ρ, (2)
где Q – объем выпуска (производства); A – параметр технологического уровня (фактор общей производительности); K – объем капитала; L – объем труда; α – доля капитала в производстве (0 < α < 1); ρ – параметр, связанный с эластичностью замены (ρ ≥ -1).
В наших исследованиях: Q – объем отгруженных товаров собственного производства муниципального района, K – стоимость основных фондов с учетом износа, L – среднегодовая численность работников предприятий.
Расчеты проведены в программе Microsoft Excel с использованием функций «Поиск решений» и «Анализ данных». Дополнительно к параметрам модели рассчитали показатели σ и R:
- σ – эластичность замены между капиталом и трудом, определяется как: σ = 1 / (1 + ρ). Если ρ = 0, то σ = 1, и функция CES сводится к функции Кобба–Дугласа, если ρ → ∞, то σ → 0, и факторы производства становятся совершенными комплементами, если ρ → -1, то σ → ∞, и факторы становятся совершенными субститутами [6];
- R2 (0 < R2 < 1) – коэффициент детерминации, который определяет уровень соответствия данных статистической модели: чем значение R2 ближе к 1, тем лучшее соответствие модели данным.
Результаты и обсуждение
На основе модели (2) определены ожидаемые значения показателей результативности Qpred (объема отгруженных товаров собственного производства добывающих муниципальных районов и республики в целом) при известных факторах стоимости основных фондов K и среднегодовой численности работающих на предприятиях L (рис. 2).
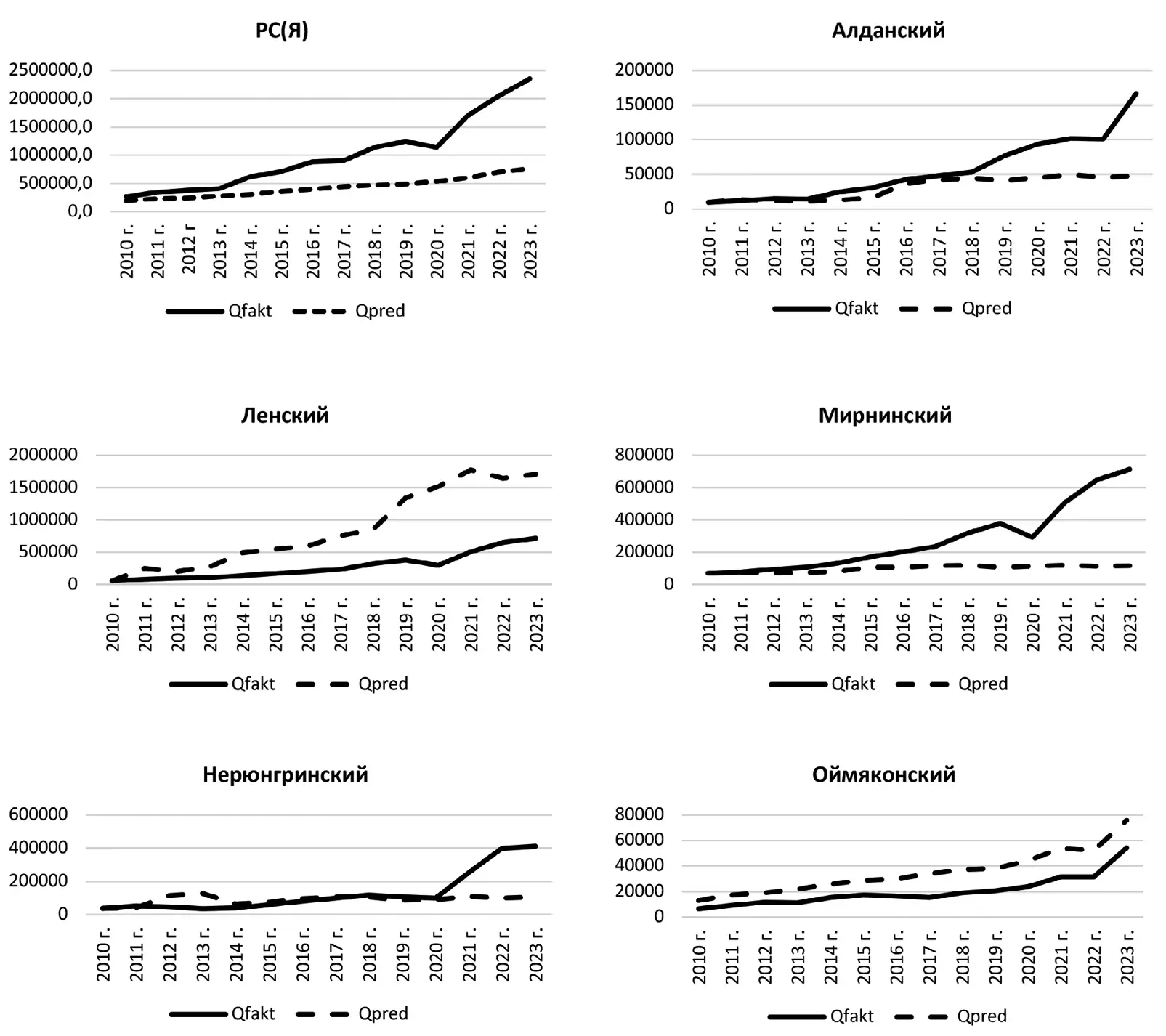 Рис. 2 Сравнительная динамика фактических Qfakt и ожидаемых Qpred значений показателей объема отгруженных товаров собственного производства добывающих муниципальных районов Республики Саха (Якутия) за 2010–2023 гг., млн руб.
Рис. 2 Сравнительная динамика фактических Qfakt и ожидаемых Qpred значений показателей объема отгруженных товаров собственного производства добывающих муниципальных районов Республики Саха (Якутия) за 2010–2023 гг., млн руб. В данном исследовании ожидаемое значение результативного показателя определяет степень эффективности использования факторов производства (основных фондов и рабочей силы) и сбалансированность развития отраслей экономики (чем ближе Qfact к Qpred, тем эффективнее производство). При резких различиях результативных показателей следует обратить внимание на косвенные производственные факторы (менеджмент, технологии и др.), также на влияние экономических и политических кризисов, рыночной конъюнктуры.
Результаты расчетов параметров производственной функции приведены в табл. 2.
| Муниципальные районы | A | α | ρ | σ | R² |
|---|---|---|---|---|---|
| РС(Я) | 1,03 | 0,51 | 0,64 | 2,78 | 0,99 |
| Алданский | 1,11 | 0,53 | 0,77 | 4,26 | 0,82 |
| Ленский | 1,07 | 0,53 | 0,72 | 3,54 | 0,83 |
| Мирнинский | 1,03 | 0,51 | 0,62 | 2,63 | 0,58 |
| Нерюнгринский | 1,04 | 0,52 | 0,64 | 2,78 | 0,32 |
| Оймяконский | 1,04 | 0,52 | 0,64 | 2,76 | 0,81 |
Анализ расчетов показывает:
- наибольшая сбалансированность наблюдается в Алданском (R² = 0,82) и Ленском (R² = 0,83) районах, где модель хорошо объясняет зависимость между затратами и выпуском;
- отставание фактических показателей от прогнозируемых в Ленском и Оймяконском районах свидетельствует о неполной загрузке мощностей или неоптимальном распределении труда и капитала;
- превышение фактического значения в Мирнинском и в целом по республике говорит о локальной эффективности использования факторов производства;
- в Мирнинском районе (R² = 0,58) и особенно в Нерюнгринском (R² = 0,32) отмечается слабая объясняющая способность модели, что может быть связано с высокой волатильностью добычи угля и алмазов или недостаточностью данных;
- в целом по республике модель демонстрирует почти идеальное соответствие (R² = 0,99), что подтверждает ее применимость для макроуровневого анализа.
Заключение
Проведенное исследование позволило разработать многофакторную модель, оценивающую влияние добывающей промышленности на социально-экономическое развитие муниципальных районов Республики Саха (Якутия). На основе производственной функции CES с постоянной эластичностью замены факторов (капитала и труда) были проанализированы пять ключевых добывающих районов, обеспечивающих более 90% объема добычи полезных ископаемых в регионе. Стоит отметить, что ограничения исследования связаны с недостатком муниципальной статистики, что сужает выбор факторов модели. Для повышения точности прогнозов требуются дополнительные данные, включая экологические, инфраструктурные и социальные показатели.
Разработанная модель может быть использована органами государственного управления и недропользователями для: оптимизации инвестиций в основные фонды и трудовые ресурсы, разработки стратегий устойчивого развития добывающих территорий, минимизации рисков перекосов в экономике локальных территорий.
Перспективы дальнейших исследований включают расширение модели за счет интеграции социальных и экологических параметров, а также применение методов машинного обучения для учета нелинейных зависимостей.
Таким образом, исследование подтверждает, что добывающая промышленность остается ключевым драйвером экономики Якутии, но требует дифференцированного подхода к управлению на локальном уровне для обеспечения сбалансированного роста.
Примечания
- [сноска1] Функция CES. Режим доступа: https://new.1-fm.ru/?id=281&t=1943 (дата обращения 12.03.2025).
- [сноска2] Федеральная служба государственной статистики по Республике Саха (Якутия). Режим доступа: https://14.roastat.gov.ru/ostatistics (дата обращения 20.03.2025).
Список литературы
1. Дилигенская А.Н. Математическое моделирование и анализ процессов управления производственными системами. Вестник Самарского государственного технического университета. Серия «Технические науки». 2010;18(7):14–18. Режим доступа: https://journals.eco-vector.com/1991-8542/article/view/19491 (дата обращения: 11.04.2025). Diligenskaya A.N. Mathematical modeling and analysis of the control processes of production systems. Vestnik of Samara State Technical University. Technical Sciences Series. 2010;18(7):14–18. (In Russ.) Available at: https://journals.eco-vector.com/1991-8542/article/view/19491 (accessed: 11.04.2025).
2. Муллахмедова С.С., Шахпазова Р.Д., Саралинова Д.С., Омаров З.З. Модель экономического роста Р. Солоу: генезис теории и методологии. Региональные проблемы преобразования экономики. 2019;(12):7–15. https://doi.org/10.26726/1812-7096-2019-12-7-15 Mullahmedova S.S., Shakhpazova R.D., Saralinova Ja.S., Omarov Z.Z. Solow's economic growth model: Genesis of theory and methodology. Regionalnye Problemy Preobrazovaniya Ekonomiki. 2019;(12):7–15. (In Russ.) https://doi.org/10.26726/1812-7096-2019-12-7-15
3. Жуков Р.А., Козлова Н.О., Хлынин Э.В., Городничев С.В. Экономико-математическое моделирование состояния и перспектив добычи полезных ископаемых в регионах ЦФО. Известия Тульского государственного университета. Науки о Земле. 2022;(3):354–368. Zhukov R.A., Kozlova N.O., Khlynin E.V., Gorodnichev S.V. Economic andmathematical modeling of the condition and prospects of extraction of minerals in the central federal district regions. Izvestiya Tulskogo Gosudarstvennogo Universiteta. Nauki o Zemle. 2022;(3):354–368. (In Russ.)
4. Грабовец О.В., Сидорчукова Е.В. Корреляционно-регрессионный анализ как метод обоснования управленческих решений. Экономика и социум. 2015;(6-2):633–638. Grabovets O.V., Sidorova A.V. Correlation and regression analysis as a method of substantiating management decisions. Economy and Society. 2015;(6-2):633–638. (In Russ.)
5. Скуфьина Т.П., Баранов С.В. Математико-статистическое моделирование динамики производства ВРП регионов Севера и Арктики: в поисках лучшей модели. Вопросы статистики. 2017;(7):52–64. Режим доступа: https://voprstat.elpub.ru/jour/article/view/538 (дата обращения: 11.04.2025). Skufina T.P., Baranov S.V. Mathematical and statistical modeling of the grp production dynamics in the regions of the north and the arctic: in search of a better model. Voprosy Statistiki. 2017;(7):52–64. (In Russ.) Available at: https://voprstat.elpub. ru/jour/article/view/5381 (accessed: 11.04.2025).
6. McFadden D. Constant elasticity of substitution production functions. The Review of Economic Studies. 1963;30(2):73–83. https://doi.org/10.2307/2295804
7. Acemoglu D., Restrepo P. Tasks, automation, and the rise in US wage inequality. Econometrica. 2022;90(5):1973–2016. https://doi.org/10.3982/ECTA19815
8. Hémous D., Olsen M. The rise of the machines: Automation, horizontal innovation, and income inequality. American Economic Journal: Macroeconomics. 2022;14(1):179–223. https://doi.org/10.1257/mac.20160164
9. Stiefenhofer P. The future of work and capital: analyzing AGI in a CES production model. Applied Mathematical Sciences. 2025;19(2):47–58. https://doi.org/10.12988/ams.2025.919196
10. Baqaee D.R., Farhi E. Networks, barriers, and trade. Econometrica. 2024;92(2):505–541. https://doi.org/10.3982/ECTA17513
11. Мартынова С.И., Дмитриев А.П. Производственный процесс как объект математического моделирования. В кн.: Литовский С.М. (ред.) Тезисы докладов 36-й научно-технической конференции преподавателей и студентов университета, г. Витебск, 22–23 апр. 2023 г. Витебск: Витебский государственный технологический университет; 2003. С. 23–24.
12. Кретова Ю.И., Цирульниченко Л.А. Математическое моделирование как эффективный инструмент прогнозирования и управления производственными процессами. Вестник Южно-Уральского государственного университета. Серия: Пищевые и биотехнологии. 2018;6(1):5–13. https://doi.org/10.14529/food180101 Kretova Yu.I., Tcirulnichenko L.A. Mathematical modeling as an effective instrument for production processes predication and management. Bulletin of South Ural State University, Series Food and Biotechnology. 2018, 2018;6(1):5–13. (In Russ.) https://doi.org/10.14529/food180101
13. Биккулов И.М., Самиков А.А., Герасимов И.А. Применение математического моделирования для оптимизации производственных процессов. В кн.: Боев Е.В., Кадыров Р.Р., Андриянова Н.В., Сулейманов Д.Ф., Горбунова М.А., Овсянникова И.В. (ред.) Малоотходные, ресурсосберегающие химические технологии и экологическая безопасность – 2020: сб. материалов 3-й Всерос. науч.-практ. конф., г. Стерлитамак, 20 окт. 2020 г. Уфа: Нефтегазовое дело; 2020. С. 585–590.
14. Лемешко Е.Ю. Применение математического моделирования для оптимизации производственных процессов. Вестник науки. 2024;1(4):452–456. Режим доступа: https://www.вестник-науки.рф/article/13733 (дата обращения: 11.04.2025). Lemeshko E.Yu. Application of mathematical modeling to optimize production processes. Science Bulletin. 2024;1(4):452– 456. (In Russ.) Available at: https://www.вестник-науки.рф/article/13733 (accessed: 11.04.2025).
15. Komissarov P.V. Comprehensive assessment of the base of mathematical modelling of production business processes. European Scientific e-Journal. 2021;(8):7–23. https://doi.org/10.47451/man2021-09-001
Dabiev D.F. Assessment of the development of the mountain regions of Russia. Russian Mining Industry. 2022;(2): 81–83. (In Russ.) https://doi.org/10.30686/1609-9192-2022-2-81-83








