Моделирование тектонических нарушений с применением связей конечной жёсткости с интеграцией в CAEFidesys
 Ю.Ю. Головченко1, А.Е. Румянцев1, В.В. Лалин2, 3, М.А. Соннов4
Ю.Ю. Головченко1, А.Е. Румянцев1, В.В. Лалин2, 3, М.А. Соннов4
1 ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация
2 Санкт-Петербургский политехнический университет Петра Великого, г. Санкт-Петербург, Российская Федерация
3 Российский университет дружбы народов имени Патриса Лумумбы, г. Москва, Российская Федерация 4 ООО «Фидесис», г. Москва, Российская Федерация
Горная Промышленность №4 / 2025 стр. 78-84
Резюме: В статье представлена оригинальная методика моделирования тектонических нарушений в массивах горных пород с использованием связей конечной жёсткости, разработанная в рамках подхода метода конечных элементов. В отличие от традиционных методов, требующих явного построения геометрии разломов и сопряжения их с другими структурными элементами модели, предложенный подход позволяет задать тектонические нарушения в неявной форме. Это достигается путём введения специальных пружинных элементов между узлами сетки, обладающих регулируемой жёсткостью в определённых направлениях. Такой способ описания ослабленных зон не требует модификации основной геометрии модели, упрощает её топологию и повышает устойчивость численного расчёта. Методика реализована в виде автономной надстройки, написанной на языке Python, и используется совместно с отечественным программным комплексом CAEFidesys. Надстройка автоматически формирует список связей конечной жёсткости по заданным координатам разломов, назначает параметры жёсткости и интегрируется в расчётную схему без необходимости вмешательства в интерфейс базовой программы. Разработанный инструмент протестирован на ряде задач геомеханики и успешно верифицирован на основе сравнений с теоретическими и эмпирическими результатами. Кроме того, в статье приводятся рекомендации по выбору параметров пружинных элементов в зависимости от геологического строения массива, степени тектонической нарушенности и особенностей инженерной задачи. Разработанная методика может быть эффективно использована при проектировании горных выработок, инженерной оценке устойчивости пород в сейсмоактивных районах, а также при геомеханическом сопровождении освоения месторождений. Её применение особенно актуально в условиях сложной геологической структуры и наличия множественных пересекающихся разломов, где классические методы моделирования сталкиваются с серьёзными вычислительными и методологическими ограничениями.
Ключевые слова: тектонические нарушения, численное моделирование, метод конечных элементов, связи конечной жёсткости, CAEFidesys, ослабленные зоны, геомеханика, пружинные элементы, инженерная геология
Для цитирования: Головченко Ю.Ю., Румянцев А.Е., Лалин В.В., Соннов М.А. Моделирование тектонических нарушений с применением связей конечной жёсткости с интеграцией в CAE Fidesys. Горная промышленность. 2025;(4): 78–84. https://doi.org/10.30686/1609-9192-2025-4-78-84
Информация о статье
Поступила в редакцию: 09.05.2025
Поступила после рецензирования: 18.06.2025
Принята к публикации: 21.06.2025
Информация об авторах
Головченко Юрий Юрьевич – научный сотрудник лаборатории геотехники, ООО «Институт Гипроникель», г. СанктПетербург, Российская Федерация; https://orcid.org/0000-0003-2980-2173; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Румянцев Александр Евгеньевич – кандидат технических наук, заведующий лабораторией геотехники, ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация; https://orcid.org/0000-0002-2204-961X; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Лалин Владимир Владимирович – доктор технических наук, профессор, Санкт-Петербургский политехнический университет Петра Великого, г. Санкт-Петербург, Российская Федерация;Российский университет дружбы народов имени Патриса Лумумбы, г. Москва, Российская Федерация; https://orcid.org/0000-0003-3850-424X
Соннов Максим Александрович – действительный член Академии горных наук, заместитель генерального директора ООО «Фидесис», г. Москва, Российская Федерация; https://orcid.org/0009-0004-3932-5571; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Введение
Моделирование тектонических нарушений в массивах горных пород представляет собой одну из ключевых задач современной геомеханики. Тектонические разломы существенно влияют на напряжённо-деформированное состояние массива, гидродинамические процессы и устойчивость горных выработок, особенно в условиях сложной геологической структуры и высокой сейсмической активности [1; 2]. Традиционные подходы к моделированию разломов, основанные на упрощённых схемах или эмпирических зависимостях, зачастую не обеспечивают необходимой точности при прогнозировании поведения массива вблизи тектонических нарушений [3].
В последние годы наблюдается активное развитие численных методов, позволяющих более точно учитывать влияние тектонических разломов на механическое поведение горных пород. Особое внимание уделяется методу конечных элементов (МКЭ), который зарекомендовал себя как эффективный инструмент для решения задач геомеханики [4]. Однако стандартные реализации МКЭ не всегда позволяют адекватно моделировать поведение разломов, особенно в случаях их сложной геометрии и неоднородных механических свойств [5].
Одним из перспективных направлений является применение связей конечной жёсткости для моделирования тектонических нарушений. Данный подход позволяет учитывать ослабленные зоны в расчётной схеме, моделируя разломы как элементы с пониженной жёсткостью, что обеспечивает более реалистичное воспроизведение их влияния на напряжённо-деформированное состояние массива [6; 7]. Применение связей конечной жёсткости также упрощает процесс построения моделей, снижая требования к качеству сетки и позволяя эффективно учитывать сложную геометрию разломов [8].
В последние годы в зарубежной научной литературе наблюдается устойчивый интерес к численному моделированию тектонических нарушений с учётом конечной жёсткости. В работах исследуются механизмы изгиба, скольжения и проскальзывания вблизи разломов с помощью двумерных и трёхмерных конечных элементных моделей, позволяющих учитывать сложную геомеханику взаимодействия слоёв литосферы [9; 10]. Отдельное внимание уделяется влиянию порового давления и его скорости изменения на индуцированное скольжение, что имеет важное значение для оценки сейсмических рисков [11]. Современные обзоры подчёркивают необходимость моделирования больших деформаций в геосреде с использованием методов, адаптированных к жёстким материалам [12], а также важность верификации численных моделей с помощью полуаналитических решений [13].
Отечественные исследования также подтверждают эффективность применения связей конечной жёсткости для моделирования тектонических нарушений. В работе [14] рассмотрены методы моделирования и управления надёжностью функционирования горных выработок, включая численные подходы к учёту тектонических разломов.
Исследование [15] посвящено геопространственному моделированию рельефа местности и тектонической нарушенности массива горных пород, предлагая методику построения трёхмерной модели рельефа с прогнозной оценкой тектонической нарушенности. В статье [16] анализируются геодинамически активные структуры западного фланга Талнахской тектономагматической системы, подчёркивая необходимость учёта тектонических нарушений при проектировании горных работ. Работа [17] описывает построение 1D геомеханической модели для сложных горно-геологических условий на примере месторождения Южного Каспия, учитывая влияние тектонических нарушений.
В исследовании [18] представлен анализ напряжённодеформированного состояния моделей разрывных нарушений с использованием метода конечных элементов.
Несмотря на значительный прогресс в данной области, остаются нерешёнными вопросы, связанные с выбором параметров связей конечной жёсткости, их калибровкой на основе геологических и геофизических данных, а также интеграцией разработанных моделей в существующие программные комплексы для численного моделирования.
Настоящая работа направлена на разработку методики задания тектонических нарушений с использованием связей конечной жёсткости в рамках метода конечных элементов с использованием CAE Fidesys. Предложенный подход позволяет учитывать геометрию и механические свойства разломов, обеспечивая более точное моделирование их влияния на напряжённо-деформированное состояние массива. В работе представлены результаты численного моделирования, демонстрирующие эффективность разработанной методики, а также рекомендации по выбору параметров связей конечной жёсткости.
Методика моделирования тектонических нарушений при помощи связей конечной жесткости
Моделирование тектонических нарушений в численных моделях при помощи твёрдых тел сопряжено с рядом трудностей как с точки зрения постановки задачи, так и в части её вычислительной реализации. Одной из ключевых проблем является необходимость точного геометрического сопряжения многочисленных тектонических нарушений между собой, особенно в условиях сложной геологической обстановки (рис. 1). При этом важно обеспечить корректное отображение как формы, так и пространственной ориентации каждой из разломных структур, что требует значительных временных и вычислительных ресурсов.
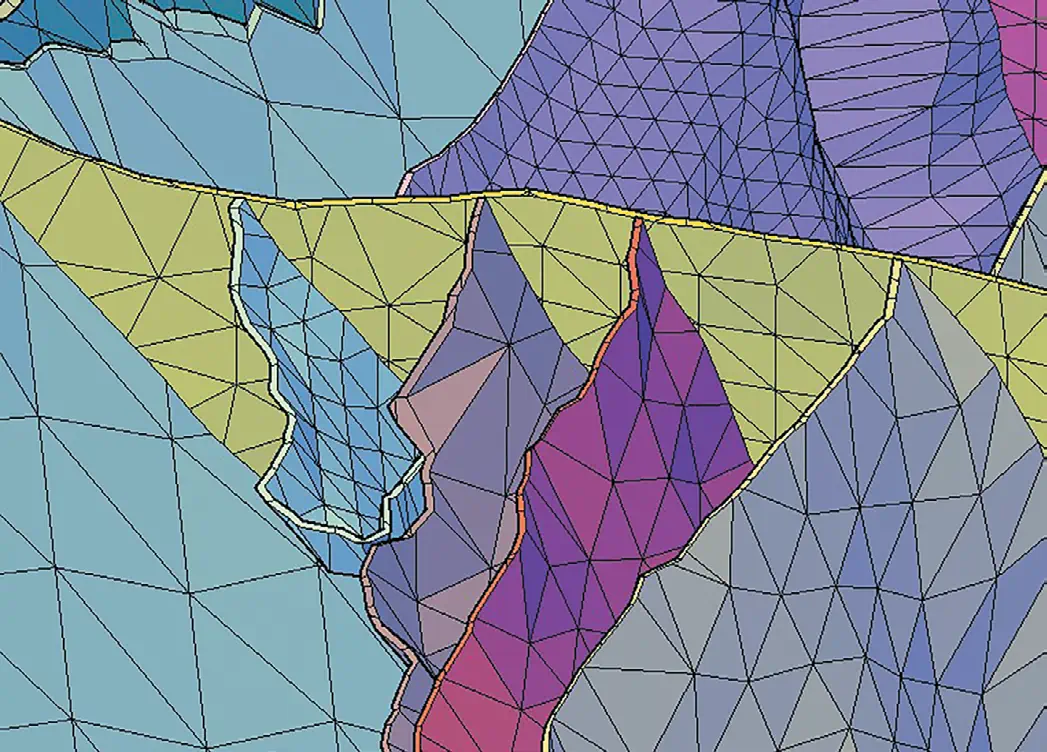 Рис. 1 Сопряжение тектонических нарушений, моделируемых твердыми телами
Рис. 1 Сопряжение тектонических нарушений, моделируемых твердыми телами
Fig. 1 Integration of tectonic faults modeled by rigid bodies
Дополнительные сложности возникают при необходимости моделирования участков пересечения тектонических нарушений с другими геологическими телами, в частности, с отрабатываемыми или разрабатываемыми горными массивами. Для этого, как правило, приходится создавать дополнительные геометрические объекты, точно соответствующие зонам пересечения (рис. 2). Эти объекты должны быть согласованы с общей сеткой конечных элементов и обладать соответствующими физико-механическими свойствами, отражающими ослабленную зону. Подобные задачи требуют высокой точности в построении расчетной схемы и продуманного выбора параметров модели, а также могут существенно усложнять её топологию, что, в свою очередь, влияет на сходимость и стабильность численного решения.
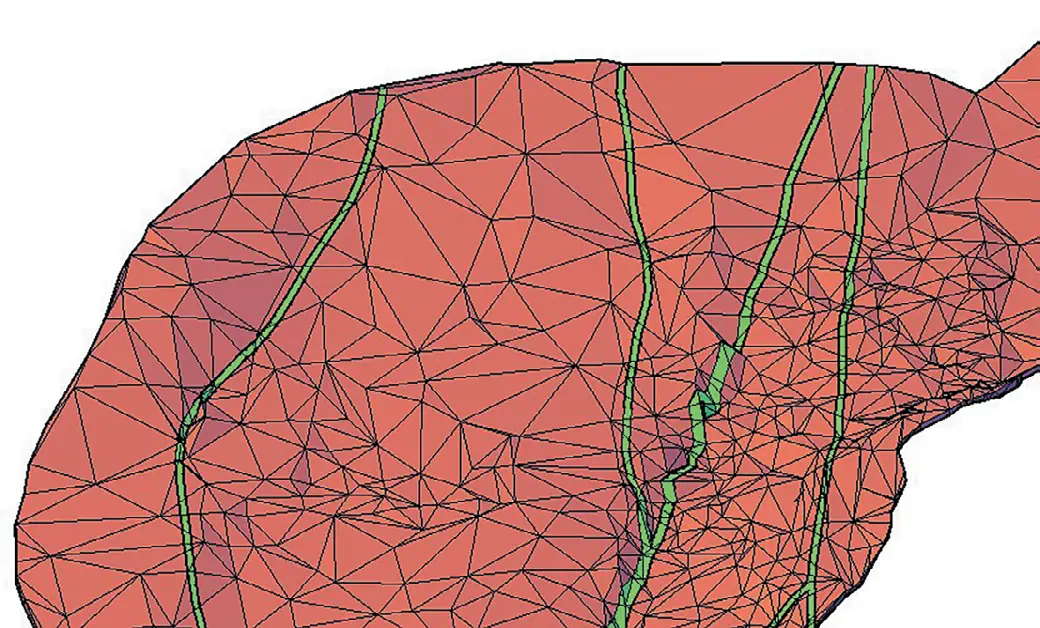 Рис. 2 Участки пересечения тектонических нарушений и отрабатываемого массива (зеленый цвет)
Рис. 2 Участки пересечения тектонических нарушений и отрабатываемого массива (зеленый цвет)
Fig. 2 Intersection areas of tectonic faults and the mined rock mass (green color)Для снижения трудоёмкости моделирования тектонических нарушений была разработана новая методика, позволяющая задавать их в неявной форме, без необходимости явного построения геометрии разломов. В основе данной методики лежит применение связей конечной жёсткости (так называемых «пружин»), которые вводятся в расчётную модель как элементы, связывающие узлы сетки и обладающие заданной жёсткостью в одном или нескольких направлениях (рис. 3).
 Рис. 3 Связи конечной жесткости
Рис. 3 Связи конечной жесткости
Fig. 3 Links offinitestiffness
Такая формализация позволяет моделировать ослабленные зоны, соответствующие тектоническим разломам, путём локального уменьшения жёсткости в определённых направлениях с учётом мощности тектонического нарушения без необходимости внесения критических изменений в основную геометрию массива. Благодаря этому существенно упрощается процесс построения моделей, особенно в случаях со сложной конфигурацией разломов или их множественными пересечениями.
Кроме того, использование связей конечной жёсткости обеспечивает гибкость при задании параметров – жёсткость можно варьировать в зависимости от геологических данных, а также учитывать анизотропию, неоднородность и различные стадии развития разломных зон.
Такой подход позволяет имитировать как полное разрушение сцепления пород по плоскости нарушения, так и частичную деградацию механических свойств, что делает модель более реалистичной и адаптируемой к различным геомеханическим сценариям.
Методика эффективно интегрируется в существующие программные комплексы (например, CAE Fidesys), основанные на методе конечных элементов, и демонстрирует высокую вычислительную эффективность при сохранении достоверности результатов, что делает её перспективной для широкого применения в задачах инженерной геологии, горного дела и сейсмостойкого проектирования.
Общая методика задания тектонических нарушений связями конечной жесткости сводится к следующим шагам:
1. Моделирование геометрии тектонических нарушений в САПР AutoCAD или аналогах в виде трехгранной сети.
2. Разрезка твердых тел численной модели по местам прохождения тектонических нарушений.
3. Генерация конформной сетки конечных элементов в численной модели и разрыв узлов по плоскостям разрезов.
4. Определение основных характеристик тектонического нарушения (толщина и модуль упругости).
5. Вычисление эквивалентных жесткостей для каждой пары узлов тектонического нарушения. Вычисление производится для локальной системы координат каждой связи, где OYлок – ось, перпендикулярная плоскости тектоники в данной точке, OYлок и OYлок – оси, находящиеся в плоскости тектоники в данной точке.
Расчет жесткостей выполняется по формулам:
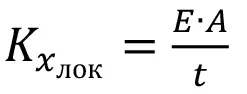 ; (1)
; (1)
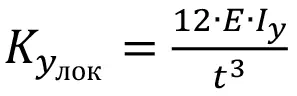 ; (2)
; (2)
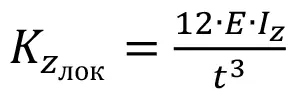 . (3)
. (3)
где E – модуль упругости тектоники, Па; A– площадь эквивалентного участка, м2; Iy, Iz – моменты инерции относительно локальных осей, м4; t – мощность тектоники, м. Фактически используемые формулы являются элементами матрицы жесткости стержня Бернулли–Эйлера, которые соответствуют перемещению стержня по трем направлениям.
6. Задание связей конечной жесткости по трем направлениям для каждой пары узлов. Верификация методики в CAEFidesys Для верификации методики был выполнен расчет бруса с ослабленным участком (эквивалент тектонического нарушения) правильной формы. Общий вид и размеры расчетной схемы приведены на рис. 4.
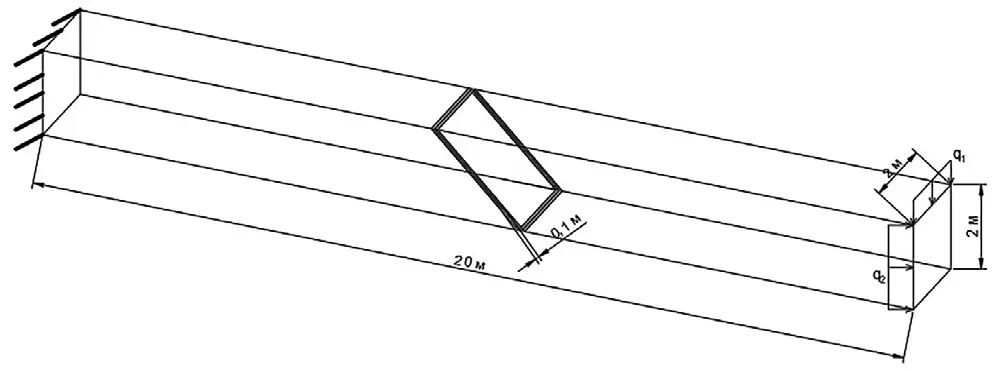 Рис.4. Общий вид расчетной схемы
Рис.4. Общий вид расчетной схемы
Fig. 4 A general view of the computational model
Брус жестко заделан с одной стороны и загружен двумя распределенными силами (q1=100000 Н/м, q2=50000 Н/м) с другой. Модуль упругости основной части бруса Eбруса = 1010 Па, модуль упругости ослабленной зоны Eконт = 108 Па. В результате сформированы и рассчитаны две модели: с ослабленной зоной, заданной твердым телом, и с ослабленной зоной, заданной связями конечной жесткости.
Общий вид численной модели приведен на рис. 5.
 Рис.5 Общий вид численной модели
Рис.5 Общий вид численной модели
Fig. A general view of the numerical model
Сравнение моделей выполнялось по максимальному значению перемещений по осям OX, OY, OZ. Результаты расчета приведены на рис. 6–8.
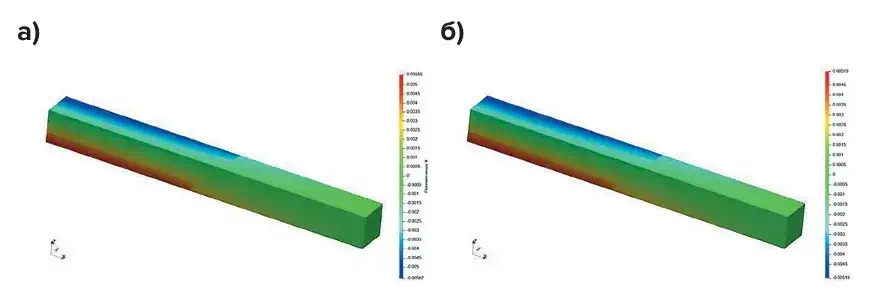 Рис. 6 Сравнение перемещений по OX: а – твердое тело, δmax = – 0,00562 м; б – связи конечной жесткости, δmax = – 0,00519 м
Рис. 6 Сравнение перемещений по OX: а – твердое тело, δmax = – 0,00562 м; б – связи конечной жесткости, δmax = – 0,00519 м
Fig. 6 Comparison of displacements along OX: а – a solid body, δmax = – 0,00562 m; б – links of finite stiffness, δmax = – 0,00519m
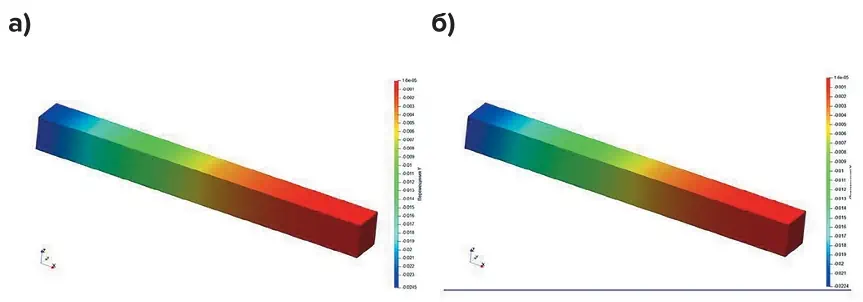 Рис. 7 Сравнение перемещений по OY: а – твердое тело, δmax = – 0,0245 м; б – связи конечной жесткости, δmax = – 0,0224 м
Рис. 7 Сравнение перемещений по OY: а – твердое тело, δmax = – 0,0245 м; б – связи конечной жесткости, δmax = – 0,0224 м
Fig. 7 Comparison of displacements along OY: а – a solid body, δmax = – 0,0245m; б – links of finite stiffness, δmax = – 0,0224m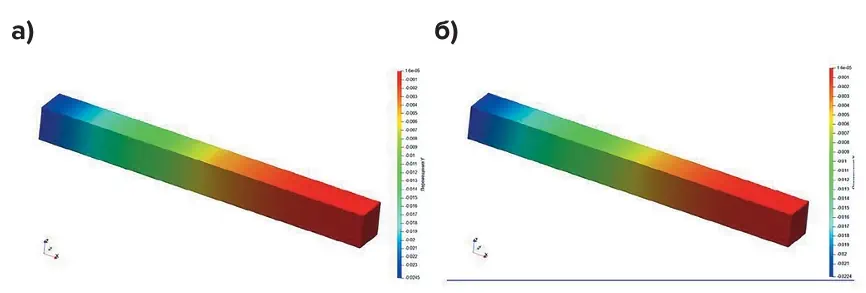 Рис. 8 Сравнение перемещений по OZ: а – твердое тело, δmax = – 0,0462 м; б – связи конечной жесткости, δmax = – 0,0447 м
Рис. 8 Сравнение перемещений по OZ: а – твердое тело, δmax = – 0,0462 м; б – связи конечной жесткости, δmax = – 0,0447 м
Fig. 8 Comparison of displacements along OZ: а – a solid body, δmax = – 0,0462m; б – links of finite stiffness, δmax = – 0,0447m
Вычислим погрешности для перемещений по каждой из осей:
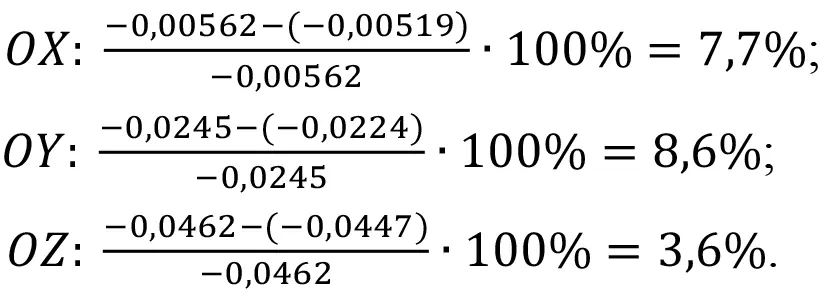
Как видно по результатам расчетов, погрешность находится в пределах нормы. Незначительное превышение инженерной погрешности в 5% в данной ситуации сопряжено с накопленной погрешностью от численного интегрирования при вычислении момента инерции и погрешности чисел с плавающей точкой.
На основании верификационной задачи можно сделать вывод о корректной работе разработанной методики. С применением указанной методики сформирована и рассчитана глобальная численная модель рудника с большим количеством тектонических нарушений (рис. 9).
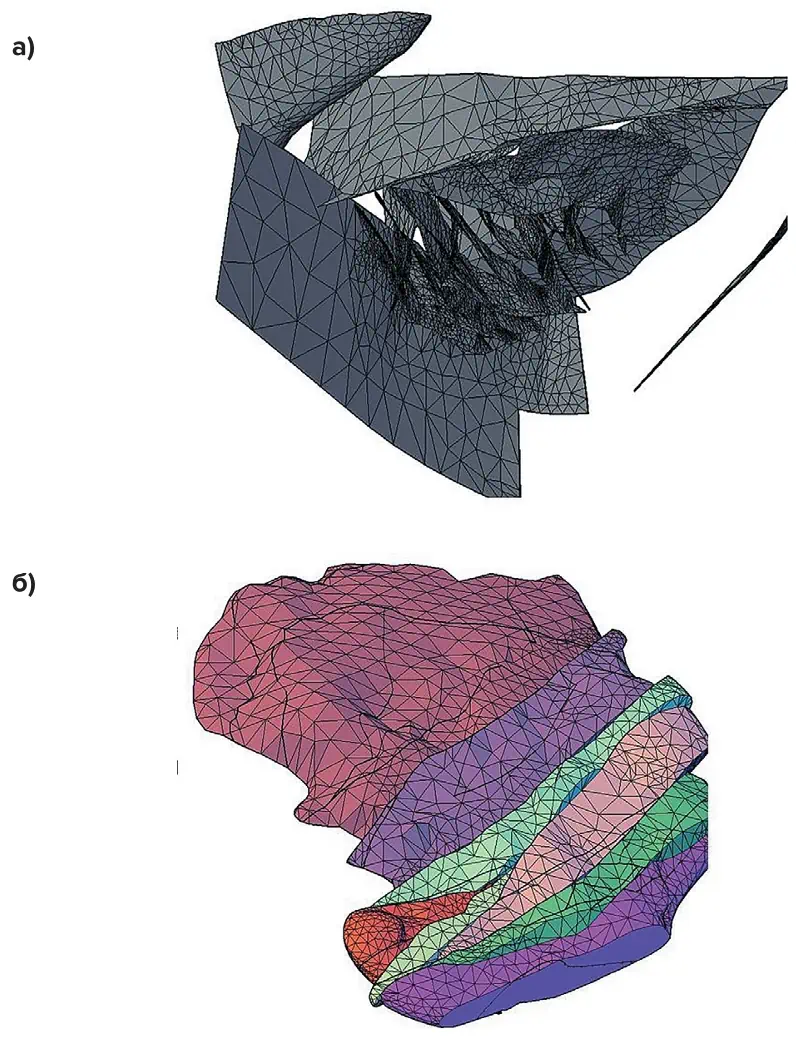 Рис.9 Формирование геометрии глобальной численной модели по предложенной методике: а – общий вид геометрии тектонических нарушений, представленных в модели, более 40 нарушений; б – общий вид геометрии интрузии с учётом тектонических нарушений для воспроизведения корректного напряженнодеформированного состояния
Рис.9 Формирование геометрии глобальной численной модели по предложенной методике: а – общий вид геометрии тектонических нарушений, представленных в модели, более 40 нарушений; б – общий вид геометрии интрузии с учётом тектонических нарушений для воспроизведения корректного напряженнодеформированного состояния
Fig. 9 Formation of the global numerical model geometry using the proposed method: а – a general view of the geometry of tectonic faults represented in the model, more than 40 faults; б – a general view of the intrusion geometry with account of the faults to reproduce the correct stressand-strain state
Так как исходное поле напряжений в руднике гравитационное, не совсем очевидно, что после ведения работ в локальных участках преобладающей компонентой тензора напряжений становится горизонтальная компонента.
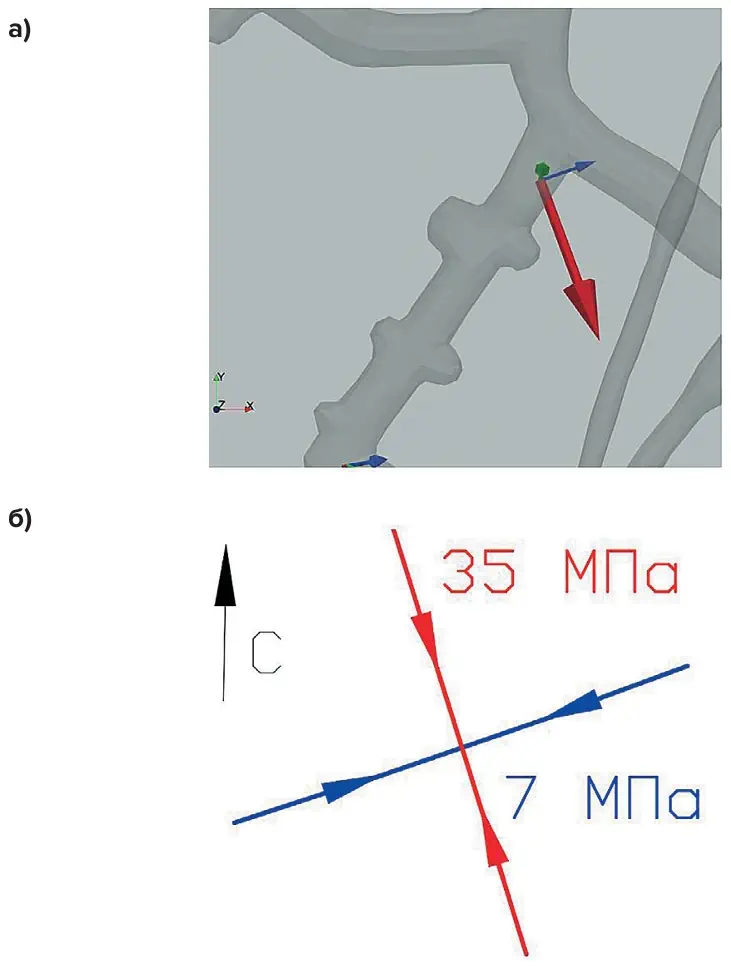 Рис.10 Сравнение локального тензора напряжений: а – численная модель; б – натурное измерение
Рис.10 Сравнение локального тензора напряжений: а – численная модель; б – натурное измерение
Fig. 10 A comparison of the local stress tensor: а – a numerical model; б – in-situ measurements
Однако при обследовании вертикальной выработки в руднике зафиксированы характерные деформации массива с преобладающей горизонтальной составляющей тензора напряжений. По результатам обследования проведена верификация расчётов в модели, где граничные условия до начала отработки были гравитационными, а после отработки до текущего состояния в модели наблюдается высокая степень сходимости результатов моделирования с фактическим состоянием в руднике (рис. 10) как по ориентации компонент тензора напряжений, так и по их значениям. Таким образом, применение предложенной методики не только позволяет формировать сложные глобальные численные модели с учётом тектонических нарушений, но и позволяет довольно точно описывать процессы перераспределения напряжений в результате ведения добычных работ с их учётом.
Заключение
Представлена и обоснована новая методика моделирования тектонических нарушений с использованием связей конечной жёсткости. Этот подход позволяет задавать ослабленные зоны, соответствующие разломам, в неявной форме, что существенно снижает трудоёмкость подготовки расчётных моделей. Вместо явного моделирования геометрии каждого тектонического нарушения предлагается использование специальных связей – пружин с заданной жёсткостью в определённом направлении, которые воспроизводят механическое поведение ослабленных участков массива.
Для практической реализации разработанной методики создана специализированная надстройка к программному комплексу CAEFidesys. Надстройка выполнена в виде внешнего программного модуля на языке Python и обеспечивает возможность автоматического добавления связей конечной жёсткости в расчётную сетку. Это делает методику гибкой и удобной в использовании, позволяя адаптировать её к различным инженерным задачам и условиям.
Проведённая верификация разработанного инструмента на ряде тестовых задач показала высокую точность воспроизведения напряжённо-деформированного состояния в присутствии тектонических нарушений. Методика также была успешно опробована в реальных инженерных проектах, что подтвердило её прикладную ценность и работоспособность.
Таким образом, предложенное решение представляет собой эффективный инструмент для численного моделирования тектонических нарушений и может быть использовано в задачах геомеханического анализа при проектировании и эксплуатации горнотехнических и инфраструктурных объектов, расположенных в зонах со значительным количеством тектонических нарушений.
Список литературы
1. Weiss R., Gandolfi S. Nuclear three-body short-range correlations in coordinate space. arXiv:2301.09605. https://doi.org/10.48550/arXiv.2301.09605
2. Егорова И.В. Перспективы мирового рынка природного урана. Руды и металлы. 2023;(1):6–16. https://doi. org/10.47765/0869-5997-2023-10001 Egorova I.V. Prospects for the natural uranium world market. Ores and Metals. 2023;(1):6–16. (In Russ.) https://doi.org/10.47765/0869-5997-2023-10001
3. Сендеров С.М. Воспроизводство минерально-сырьевой базы ТЭК как важнейшая составляющая обеспечения энергетической безопасности России. В кн.: Методические вопросы исследования надежности больших систем энергетики: материалы 96-го заседания Международного научного семинара им. Ю.Н. Руденко, г. Архангельск, 15–19 июля 2024 г. Иркутск: Институт систем энергетики им. Л.А. Мелентьева СО РАН; 2024. С. 40–50.
4. Ибламинов Р.Г. Геолого-промышленные типы месторождений полезных ископаемых. Рудные месторождения. Пермь: ПГНИУ; 2021. 278 с. Режим доступа: https://elis.psu.ru/node/642780 (дата обращения: 21.04.2025).
5. Никитенко С.М., Патраков Ю.Ф., Никитенко М.С., Кизилов С.А., Харлампенкова Ю.А. Геотехнологические перспективы использования радиационных свойств угля и породы. Физико-технические проблемы разработки полезных ископаемых. 2021;(6):181–189. https://doi.org/10.15372/FTPRPI20210617 Nikitenko S.M., Patrakov Y.F., Nikitenko M.S., Kizilov S.A., Kharlampenkova Y.A. Radiation properties of coal and barren rocks: geotechnical applications. Journal of Mining Science. 2021;57(6):1041–1048. https://doi.org/10.1134/S106273912106017X
6. Юдович Я.Э., Кетрис М.П. Уран в углях. Сыктывкар; 2001. 84 с.
7. Сидорова Г.П., Крылов Д.А. Радионуклиды в углях и продуктах их сжигания. Медицинская радиология и радиационная безопасность. 2016;61(2):75–78. Режим доступа: https://medradiol.fmbafmbc.ru/issues?id=328 (дата обращения: 21.04.2025). Sidorova G.P., Krylov D.A. Radioactive elements in coals and their combustion products. Medical Radiology and Radiation Safety. 2016;61(2):75–78. Available at: https://medradiol.fmbafmbc.ru/issues?id=328 (accessed: 21.04.2025).
8. Арбузов С.И., Ильенок С.С., Чекрыжов И.Ю. Радиоактивные элементы (U, TH) в углях Северной Азии. В кн.: Язиков Е.Г. (ред.) Радиоактивность и радиоактивные элементы в среде обитания человека: материалы 4-й Международной конференции, г. Томск, 20–24 сент. 2021 г. Томск: Национальный исследовательский Томский политехнический университет; 2021. С. 55–62.
9. Борисенко Д.И., Семенов Е.В. Экономический ущерб от подземных пожаров в Китае и России. В кн.: Наука и общество 2019: материалы Национальной научной конференции с международным участием, г. Кърджали (Болгария), 2-3 окт. 2019 г. Кърджали: Издава «РКР Принт» ООД; 2019. Т. 7. С. 495–500.
10. Менделеев Д.И. Нефтяная промышленность в Северо-Американском штате Пенсильвании и на Кавказе. СПб.: тип. т-ва «Обществ. польза»; 1877. 304 с.
11. Ковальчук М.В., Нарайкин О.С., Яцишина Е.Б. Природоподобные технологии: новые возможности и новые вызовы. Вестник Российской академии наук. 2019;89(5):455–465. https://doi.org/10.31857/S0869-5873895455-465 Kovalchuk M.V., Naraikin O.S., Yatsishina E.B. Nature-like technologies: new opportunities and new challenges. Vestnik Rossiiskoy akademii nauk. 2019;89(5):455–465. (In Russ.) https://doi.org/10.31857/S0869-5873895455-465
12. Волков В.Г., Чесноков А.В.; Пономарев-Степной Н.Н. (ред.) Реабилитация радиационного наследия. Научно-технический опыт Курчатовского института. М.: ИздАТ; 2008. 119 с.
13. Новоселов С.В., Попов В.Б., Голик А.С. Оценка риска возникновения эндогенных пожаров в угольных шахтах. Уголь. 2020;(5):21–25. https://doi.org/10.18796/0041-5790-2020-5-21-25 Novoselov S.V., Popov V.B., Golik A.S. Risk assessment of endogenous fires in coal mines. Ugol’. 2020;(5):21–25. (In Russ.) https://doi.org/10.18796/0041-5790-2020-5-21-25
14. Голынская Ф.А. Степень метаморфизма как главный генетический признак самовозгорающихся углей. Горный информационно-аналитический бюллетень. 2013;(7):164–169. Режим доступа: https://giab-online.ru/files/Data/2013/7/164-169-Golinskaya_-_6_str.pdf (дата обращения: 21.04.2025). Golynskaya F.A. Metamorphism intensity as the main genetic trait of self-combustion coal. Mining Informational and Analytical Bulletin. 2013;(7):164–169. (In Russ.) Available at: https://giab-online.ru/files/Data/2013/7/164-169-Golinskaya_-_6_str.pdf (accessed: 21.04.2025).
15. Сидорова Г.П., Маниковский П.М., Якимов А.А., Овчаренко Н.В. Оценка потенциальной опасности углей и отходов их переработки на угольных месторождениях Приаргунской группы Забайкальского края. Горный информационноаналитический бюллетень. 2024;(12):62–77. Режим доступа: https://giab-online.ru/files/Data/2024/12/12_2024_62-77. pdf (дата обращения: 21.04.2025). Sidorova G.P., Manikovskiy P.M., Yakimov A.A., Ovcharenko N.V. Hazard assessment of coals and processing waste in the Argun area in Transbaikalia. Mining Informational and Analytical Bulletin. 2024;(12):62–77. (In Russ.) Available at: https://giab-online.ru/files/Data/2024/12/12_2024_62-77.pdf (accessed: 21.04.2025).
16. Голынская Ф.А. Оценка геологических факторов самовозгорания углей ведущих угольных бассейнов. Горный информационно-аналитический бюллетень. 2010;(11):193–203. Режим доступа: https://giab-online.ru/files/Data/2010/11/Golynskaya_11_2010.pdf (дата обращения: 21.04.2025). Golynskaya F.A. The evaluation of coal ignitability factors at the largest coal basins. Mining Informational and Analytical Bulletin. 2010;(11):193–203. (In Russ.) Available at: https://giab-online.ru/files/Data/2010/11/Golynskaya_11_2010.pdf (accessed: 21.04.2025).
17. Крылов Д.А., Сидорова Г.П. Оценка содержания радиоактивных элементов в углях и продуктах их сжигания. Горный информационно-аналитический бюллетень. 2015;(7):369–376. Krylov D.A., Sidorova G.P. Evaluation of the content of radioactive elements in coals and products of combustion. Mining Informational and Analytical Bulletin. 2015;(7):369–376. (In Russ.)
18. Anghelescu L., Diaconu B.M. Advances in detection and monitoring of coal spontaneous combustion: techniques, challenges, and future directions. Fire. 2024;7(10):354. https://doi.org/10.3390/fire7100354
19. Коршунов Г.И., Мироненкова Н.А., Полещук А.А. Актуальные методы определения очагов самовозгорания на угольных шахтах. Горный информационно-аналитический бюллетень. 2025;(5):169–180. Режим доступа: https://giabonline.ru/files/Data/2025/5/04_2025_169-180.pdf (дата обращения: 21.04.2025). Korshunov G.I., Mironenkova N.A., Poleshchuk A.A. The topical methods of detecting spontaneous combustion sources in coal mines. Mining Informational and Analytical Bulletin. 2025;(5):169–180. (In Russ.) Available at: https://giab-online.ru/files/Data/2025/5/04_2025_169-180.pdf (accessed: 21.04.2025).
20. Борисенко Д.И. Акустический способ диагностики очагов пожаров в угольных пластах. Уголь. 2013;(9):44–45. Borisenko D.I. Acoustic method of the fire centers diagnostics in coal layers. Ugol’. 2013;(9):44–45. (In Russ.)
21. Kong B., Zhong J., Lu W., Hu X., Gao L., Zhuang Z. et al. Progress in the study of acoustic effects and precursor characteristics during spontaneous combustion of coal. Coal Science and Technology. 2025;53(2):211–221. (In Chinese) https://doi.org/10.12438/cst.2024-0157
22. Lee M.R. et al. Vibroseis application becoming world-wide. World Petroleum. 1963;34(3):85.
23. Pietsch K., Slusarczyk R., Dec J. O możliwości lokalizowania stref bezpokładowych przy zastosowaniu sejsmiki węglowej. Zeszyty naukowe politechniki slaskiej. Serie: Gornictwo. 1987;155(1021):157–170.
24. Потапов С.Л. Контроль перемещения фронта горения и состояния кровли при подземном сжигании угля с использованием взрывных сигнализаторов [дис. ... канд. техн. наук]. М.; 1990. 164 с.
25. Гладун Ю.В. Разработка сейсмоакустических методов контроля границ выработанного пространства при подземном сжигании угля [автореф. дис. … канд. техн. наук]. М.; 1990. 19 с.
26. Лебедев В.А., Карабута В.С. Проблемы обеспечения радиационной безопасности в нефтедобывающей промышленности России. Молодой ученый. 2016;(1):257–261. Режим доступа: https://moluch.ru/archive/105/24728/ (дата обращения: 21.04.2025). Lebedev V.A., Karabuta V.S. Problems of the provision of the radiation safety in the oil industry of Russia. Molodoi Uchenyi. 2016;(1):257–261. (In Russ.) Available at: https://moluch.ru/archive/105/24728/ (accessed: 21.04.2025).








