Прогноз водно-теплового режима прибортового и подкарьерного массивов карьеров криолитозоны

Е.К. Романова
Институт горного дела Севера им. Н.В. Черского Сибирского отделения Российской академии наук, г. Якутск, Российская Федерация
Russian Mining Industry №4S / 2025 p. 73-77

Резюме: Цель работы – установление закономерностей формирования температурного и влажностного режимов прибортового и подкарьерного массивов горных пород карьера криолитозоны в зависимости от геометрических размеров карьера. Компьютерная реализация задачи прогноза водно-теплового режима прибортового и подкарьерного массивов карьеров криолитозоны включает в себя разработку математической модели теплообмена, фильтрации и влагопереноса, решение поставленной задачи с помощью численных методов и компьютерных технологий. Разработана двухмерная математическая модель тепло-влагопереноса в прибортовом и подкарьерном массивах карьера криолитозоны с учетом поступления, испарения, миграции и фазового перехода влаги. Важная особенность этой модели заключается в отсутствии чётко выраженной границы между зонами полного и неполного насыщения водой, что делает её применимой для анализа сложных геологических сред. Основанная на разработанной математической модели компьютерная программа для ЭВМ позволяет сделать многолетний прогноз и провести исследование особенностей формирования температурного и влажностного режимов прибортового и подкарьерного массивов горных пород карьера криолитозоны в зависимости от различных природно-климатических условий и конструктивных параметров карьера. Проведены тестовые расчеты по оценке влияния геометрических размеров карьера на процесс формирования водного и теплового режима прибортового и подкарьерного массивов горных пород карьера.

Ключевые слова: карьер криолитозоны, прибортовой массив пород, подкарьерный массив пород, температурный режим, влажностный режим, влагоперенос

Благодарности: Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема №0297-2021-0021, ЕГИСУ НИОКТР №122011800083-0) с использованием оборудования ЦКП ФИЦ ЯНЦ СО РАН.

Для цитирования: Романова Е.К. Прогноз водно-теплового режима прибортового и подкарьерного массивов карьеров криолитозоны. Горная промышленность. 2025;(4S):73–77. https://doi.org/10.30686/1609-9192-2025-4S-73-77

Информация о статье

Поступила в редакцию: 08.06.2025

Поступила после рецензирования: 13.08.2025

Принята к публикации: 20.08.2025

Информация об авторе

Романова Елена Константиновна – кандидат технических наук, научный сотрудник, Институт горного дела Севера им. Н.В. Черского Сибирского отделения Российской академии наук, г. Якутск, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

Современные горнодобывающие предприятия активно осваивают месторождения полезных ископаемых в регионах с многолетнемерзлыми грунтами – зонах криолитозоны. Карьеры, расположенные в районах вечной мерзлоты, сталкиваются с уникальными проблемами, связанными с изменением температуры и влажности почвы, что влияет на устойчивость бортов карьера и безопасность ведения горных работ. Проблематика изучения водно-теплового режима приобретает особую значимость ввиду рисков возникновения деформаций массива, вызванных изменениями состояния грунтов вследствие колебаний температуры и влажности.

Известно, что нарушение устойчивости прибортового и подкарьерного массивов карьеров криолитозоны вызывается главным образом криогенными процессами (режеляция, сублимация, морозное пучение, осадка, растрескивание, дезинтеграция и др.) и связано с формированием сезонно-талого слоя в летний период [1]. Эти процессы могут привести к образованию трещин, разрушению откосов и возникновению чрезвычайных ситуаций, негативно влияющих на производственную деятельность предприятий. Актуальность темы обусловлена возрастающими объемами добычи минерального сырья в северных регионах России, высокими рисками техногенных катастроф и экономической целесообразностью принятия обоснованных решений относительно проектирования и эксплуатации открытых разработок в сложных климатических условиях.

Прогнозирование водно-теплового режима является важной задачей при разработке месторождений полезных ископаемых в условиях криолитозоны. Исследование закономерностей формирования влагопереноса в прибортовых и подкарьерных массивах карьеров позволяет оценить влияние геокриологических условий на эксплуатационную надежность карьеров и предложить эффективные методы мониторинга и управления состоянием массива. В настоящее время эффективным средством прогнозирования тепло-влажностного состояния массивов пород карьера является метод математического моделирования. Математическое моделирование, основанное на современных компьютерных технологиях, превратилось в универсальный инструмент изучения реальных явлений и процессов, особенно там, где проведение натурных экспериментов оказывается невозможным или чрезвычайно дорогостоящим [2–7].

Задачей настоящей работы является разработка методики многолетнего прогноза водно-теплового состояния прибортового и подкарьерного массивов карьеров криолитозоны и исследование влияния конструктивных параметров карьера на данные тепло-влажностные процессы.

Материалы и методы

Рассматривается карьер c заданными глубиной и углом откоса бортов. На дневную поверхность и дно карьера в течение года выпадает определенное количество осадков в виде снега и дождя. В зимние месяцы с октября по апрель на верхней площадке лежит снежный покров. Снег в начале мая тает. В середине каждого летнего месяца (с мая по сентябрь включительно) в течение нескольких суток идут дожди. В остальное летнее время происходит испарение влаги с поверхностей карьера.

Расчетная область для горных пород Ω имеет сложную форму в виде плоскости, ограниченной дневной поверхностью, бортом, дном карьера. Исследуемое тепло-влажностное поле в момент времени t определяется распределением температуры и полного гидравлического напора по массиву горных пород, т.е. функциями T = T(y, z, t) и Ф = Ф(y, z, t).

Математическая модель тепло-влагопереноса в прибортовом и подкарьерном массивах карьера криолитозоны с учетом поступления, испарения и миграции влаги

Тепловая часть модели

Распространение тепла в массиве горных пород, которое учитывает фазовый переход влаги и перенос теплоты вместе с движением влаги, описывается нестационарным уравнением теплопроводности следующего вида [2]:

(1)

где Т – температура пород, °С; C_эфф – эффективная теплоемкость, Дж/(м³·К); λ – коэффициент теплопроводности пород, Вт/(м·К); с_w – объемная теплоемкость воды, Дж/(м³·К);

v_wy, v_wz – скорость потока влаги по направлению y, z соответственно, м/с.

Учет теплоты фазового перехода реализуется путем задания эффективной теплоёмкости пород [2]:

(2)

где С(T) – объемная теплоемкость породы, Дж/(м³·К);

L_ф – теплота фазового перехода влаги, Дж/кг; θ – влажность пород, доли ед.; ρ – плотность пород, кг/м³; T* – температура плавления (замерзания) воды в породе, Сº, δ – функция Дирака; μ– номер фронта фазового перехода (μ = 1, ..., μ0).

Разрывность коэффициентов теплоёмкости и теплопроводности связана с процессами фазовых переходов влаги в горных породах при замораживании и оттаивании [2]:

(3)

где с_ск, ρ_ск – удельная теплоемкость, Дж/(кг∙К), плотность скелета пород, кг/м³; след, свод – удельная теплоемкость льда, воды соответственно, Дж/(кг∙К); λ_м, λ_т – коэффициент теплопроводности, Вт/(м∙К), для мерзлых (талых) пород соответственно.

Скорость потока влаги определяется законом переноса [2]:

(4)

где Ф = ψ – y – полный гидравлический напор, м; ψ – капиллярно-влажностный потенциал (поровое давление), м; kw – коэффициент влагопроводности пород, м/с.

На поверхностях карьера применяется граничное условие третьего рода, описывающее теплообмен массива пород с атмосферным воздухом с учетом толщины снежного покрова и скорости атмосферного воздуха. На границах теплового влияния и симметрии расчетной области используется граничное условие второго рода, отражающее отсутствие теплового потока. В начальный момент времени задается начальное распределение температуры в массивах горных пород.

Влажностная часть модели

Согласно литературным источникам [8; 9] влагопереносом в промерзающей зоне пород можно пренебречь ввиду особенностей фазового перехода воды при замерзании.

Влажностная задача решается только в пределах талой зоны (Т > 0 °С).

Общее дифференциальное уравнение, описывающее процессы влагопереноса и фильтрации в ненасыщеннонасыщенных породах, имеет вид [2]:

(5)

где Ф = ψ – y – полный гидравлический напор (ось у направлена вниз), м; ψ –поровое давление, м; kw – коэффициент влагопереноса, с–1; Cw – дифференциальная влагоемкость, м вод. ст.–1. Здесь Cw = 0, когда ψ ≥ 0 (насыщенность пород) и Cw = ∂ θ /∂ψ, если ψ < 0 (ненасыщенность пород); θ – объемная влажность, доли ед.

Решение уравнения (5) требует знания зависимостей коэффициентов влагопроводности kw и влагоёмкости Cw от капиллярно-влажностного потенциала ψ. Точное определение этих зависимостей повышает точность расчетов и делает возможным адекватное моделирование процессов инфильтрации, осушения и формирования зон водонасыщения.

В данной работе применяется широко используемый в моделях влагопереноса в горных породах благодаря своей универсальности и точности метод Муалема–Ван Генухтена, по которому формулы аппроксимации объемной влажности, а также вычисленного с ее помощью отношения функции гидравлической проводимости пород к коэффициенту фильтрации влаги имеют вид [10; 11]:

(6)

(7)

где θr – минимальный удельный объем жидкой воды в породах, доли ед.; θs – объемная влажность при полном насыщении водой толщи пород, доли ед.; α – эмпирический параметр, м вод. ст–1; n – эмпирический параметр; m = 1 – 1/n.

На границах симметрии расчетной области и на границах «талая зона–мерзлая зона» применяется граничное условие отсутствия перемещения влаги. На поверхностях карьера во время дождя и таяния снега устанавливается условие водонасыщения Ф = –y, а в остальное летнее время – поток влаги при испарении через поверхности карьера. На боковой границе расчётной области, пересекаемой потоком влаги, используется граничное условие неразрывности течения, выражающее равенство расходов потока слева и справа от границы. В начальный момент времени задается начальное распределение полного гидравлического напора в массиве горных пород.

Выбор математических методов решения поставленной задачи

Моделирование процессов совместного переноса тепла, влаги, замораживания и оттаивания пород представляет серьёзные сложности как теоретического, так и практического характера. Поиск эффективных математических методов для задач по тепло- и массопереносу – актуальная проблема [2].

Наиболее подходящим для численного решения многомерных задач теплообмена при наличии нескольких немонотонно движущихся фронтов является метод сквозного счета Самарского–Моисеенко. Основными преимуществами метода являются логическая простота и возможность применения большого шага по времени [12] При решении задач фильтрации и влагопереноса целесообразно применять итерационные методы, позволяющие единообразно выполнять счет в зонах полного и неполного насыщения без явного выделения границы раздела зон.

Здесь с самой наилучшей стороны зарекомендовал себя попеременно-треугольный итерационный метод, предложенный А.А. Самарским. А.Б. Кучеров и Е.С. Николаев разработали модифицированный попеременно-треугольный метод, не зависящий от равномерности шагов сетки по пространству и от экстремальных значений коэффициентов уравнения [13–15].

Программа, реализующая расчеты по разработанной математической модели теплообмена и влагопереноса в прибортовом и подкарьерном массивах горных пород карьера криолитозоны, написана в среде программирования Visual C++10 и работает в диалоговом режиме для операционных систем Microsoft Windows [16; 17].

Результаты

Тестовые расчеты проведены для климатических условий Мирнинского района Республики Саха (Якутия).

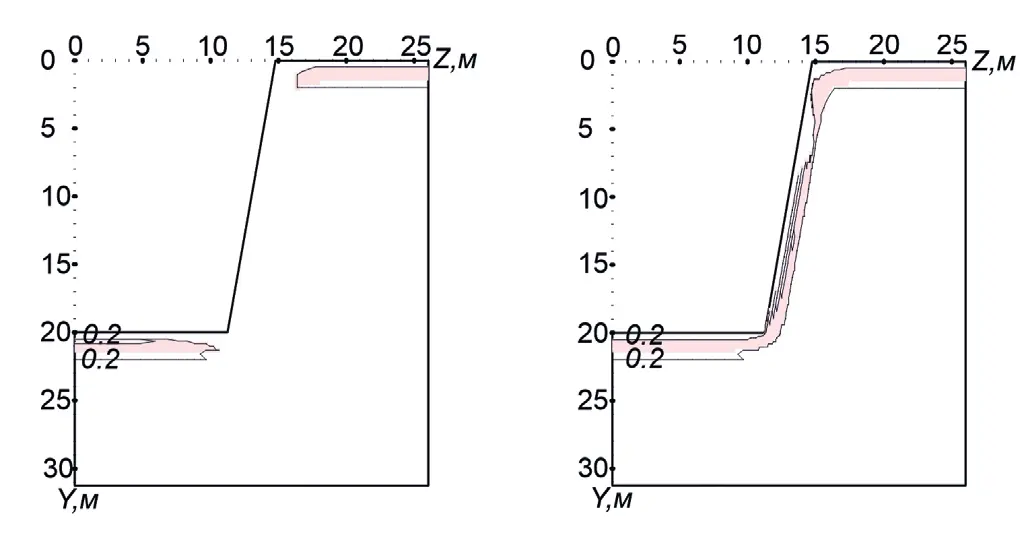Рис. 1 Распределение зон водонасыщенности в разные годы эксплуатации карьера (глубина карьера 20 м, угол откоса борта 80º): а – 2-й год; б – 20-й год

Fig. 1 Distribution of the water saturation zones in different years of the open pit mine operation (the open pit depth of 20 m, the wall slope angle of 80º): а – the 2nd year; б – the 20th year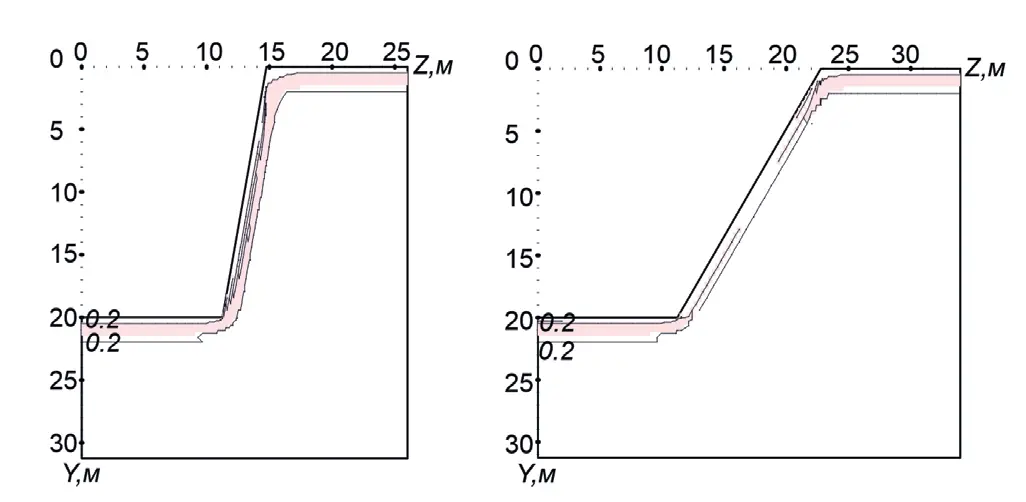Рис. 2 Распределение зон водонасыщенности при разных углах откоса борта карьера (30-й год эксплуатации карьера, глубина карьера 20 м): а – угол откоса борта 80º; б – угол откоса борта 60º

Fig. 2 Distribution of the water saturation zones at different wall slope angles (30th of the open pit mine operation, the open pit depth of 20 m): а – the wall slope angle of 80º; б – the wall slope angle of 60º

На рис. 1 и 2 приводятся результаты многолетнего прогноза водно-теплового режима прибортового и подкарьерного массивов горных пород карьера криолитозоны во время максимального оттаивания (конец сентября).

Результаты представлены в виде графиков, изображающих распределение зон из водонасыщенных талых пород. Расчеты показали, что за первый же год эксплуатации в подкарьерном массиве над мерзлой толщей пород, служащей криогенным водоупором, образовывается водонасыщенная зона, которая в результате ежегодного накопления влаги расширяется вверх по склону и после 20-го года эксплуатации смыкается с водонасыщенной надмерзлотной зоной дневной поверхности (см. рис. 1). В летнее время водонасыщенная зона оттаивает, тем самым вызывает надмерзлотный фильтрационный поток, направленный вниз по откосу борта, что способствует разрушению борта карьера и накоплению воды в подкарьерном массиве пород.

Расчеты показали, что тепло-влажностное состояние прибортового и подкарьерного массивов горных пород карьера значительно зависит от угла откоса борта карьера.

На рис. 2 видно, что при угле откоса борта 60º за 30 лет эксплуатации карьера в прибортовом массиве пород не образовалась сплошная надмерзлотная водонасыщенная зона.

В результате в летнее время отсутствует направленный вниз по склону надмерзлотный фильтрационный поток, снижающий устойчивость борта карьера.

Тестовые расчеты показали, что глубина карьера не оказывает существенного влияния на тепло-влажностное состояние прибортового и подкарьерного массивов. В случае когда угол откоса борта равен 80º, при глубине карьера 40 м, как и при глубине 20 м, после 20-го года эксплуатации в исследуемых массивах пород образовывается сплошная надмерзлотная водонасыщенная зона.

Обсуждение результатов

Проведена оценка влияния геометрических размеров карьера на многолетний процесс формирования водного и теплового режима прибортового и подкарьерного массивов горных пород карьера. Исследования показали, что угол откоса борта карьера значительно влияет на формирование тепло-влажностного режима прибортового и подкарьерного массивов горных пород карьера, в то время как глубина карьера не оказывает существенного влияния на данный тепло-влажностный процесс. При определенных условиях (угол откоса борта около 60º) можно добиться стабильного состояния массива пород без появления опасных водонасыщенных зон. Такое заключение может быть полезно при проектировании новых карьеров или анализе существующих объектов, помогая выбирать оптимальный угол наклона борта карьера, обеспечивающий устойчивость борта и безопасность эксплуатационных работ.

Заключение

Разработана двухмерная математическая модель тепло-влагопереноса в прибортовом и подкарьерном массивах карьера криолитозоны с учетом поступления, испарения, миграции и фазового перехода влаги, отличающаяся описанием процессов теплообмена и продвижения влаги без чётко выраженной границы между зонами полного и неполного насыщения водой, что делает её универсальной для исследований сложных геологических сред.

Основанная на разработанной математической модели компьютерная программа для ЭВМ позволяет сделать многолетний прогноз и провести исследование особенностей формирования температурного и влажностного режимов прибортового и подкарьерного массивов горных пород карьера криолитозоны в зависимости от различных природно-климатических условий и конструктивных параметров карьера. Разработанная методика в дальнейшем может использоваться при решении задач выбора оптимальных конструктивных параметров карьера и разработке рекомендаций по регулированию водно-теплового режима прибортового и подкарьерного массивов карьера криолитозоны в целях обеспечения безопасности горного производства.

Список литературы

1. Изаксон М.В. Управление устойчивостью уступов глубоких карьеров в многолетней мерзлоте теплоизолирующими экранами [автореф. дис. ... канд. техн. наук]. Кемерово; 2006. 22 с.

2. Романова Е.К., Соловьев Д.Е., Киселев В.В., Львов А.С. Выбор оптимальной защиты верхних бровок уступов карьеров криолитозоны от растепления. Горный журнал. 2024;(2):21–25. https://doi.org/10.17580/gzh.2024.02.03Romanova E.K., Soloviev D.E., Kiselev V.V., Lvov A.S. Selection of optimum thawing protection for bench crests in open pit mines in the permafrost zone. Gornyi Zhurnal. 2024;(2):21–25. (In Russ.) https://doi.org/10.17580/gzh.2024.02.03

3. Ткач С.М., Курилко А.С., Романова Е.К. Роль теплофизических исследований в обеспечении эффективности и безопасности эксплуатации глубоких карьеров криолитозоны. Горный информационно-аналитический бюллетень. 2015;(S56):80–85.Tkach S.M., Kurilko A.S., Romanova E.K. Effect of thermophysical research to cryolitezone deep opencast effectiveness and safety exploitation providing. Mining Informational and Analytical Bulletin. 2015;(S56):80–85. (In Russ.)

4. Романова Е.К., Курилко А.С., Киселев В.В. Управление устойчивостью уступов кимберлитовых карьеров криолитозоны с помощью теплоизолированного оградительного сооружения. Горный информационно-аналитический бюллетень. 2017;(S24):264–271. https://doi.org/10.25018/0236-1493-2017-11-24-264-271Romanova E.K., Kurilko A.S., Kiselev V.V. Cryolitezone opencast bench stability controlling with heat insulated protective structures assistance. Mining Informational and Analytical Bulletin. 2017;(S24):264–271. (In Russ.) https://doi.org/10.25018/0236-1493-2017-11-24-264-271

5. Зырянов И.В., Акишев А.Н., Бокий И.Б., Шерстюк Н.М. Общий подход к определению параметров нерабочих бортов сверхглубоких карьеров алмазорудных месторождений. Горный журнал. 2021;(2):48–53. https://doi.org/10.17580/gzh.2021.02.05Zyryanov I.V., Akishev A.N., Bokiy I.B., Sherstyuk N.M. General concept of determining the parameters of non-mining walls of ultra-deep diamond deposits development open pits. Gornyi Zhurnal. 2021;(2):48–53. (In Russ.) https://doi.org/10.17580/gzh.2021.02.05

6. Шполянская Н.А. Особенности открытой разработки месторождений в криолитозоне в условиях континентального климата. Инженерная геология. 2020;15(3):42–52. https://doi.org/10.25296/1993-5056-2020-15-3-42-52Shpolyanskaya N.A. Specific features of opencast mining in the cryolithic zone under continental climate conditions. Engineering Geology World. 2020;15(3):42–52. (In Russ.) https://doi.org/10.25296/1993-5056-2020-15-3-42-52

7. Zairov Sh.Sh., Nomdorov R.U., Ashuraliev U.T. Increasing the stability of the sides of the quarry by forming a concave profile of the slope of a high ledge. Insights in Mining Science & Technology. 2022;3(3):555617. Available at: https://juniperpublishers.com/imst/pdf/IMST.MS.ID.555617.pdf (accessed: 01.07.2025).

8. Равшанов Н., Шадманов И.У., Мирзаева Н.М. Моделирование и визуализация тепловлагопереноса в пористых средах. Проблемы вычислительной и прикладной математики. 2022;(2):72–87. Режим доступа: https://journals.airi.uz/index.php/pvpm/article/view/34 (дата обращения: 01.07.2025).Ravshanov N., Shadmanov I.U., Mirzaeva N.M. Modeling and visualization of heat and moisture transfer in porous media. Problems of Computational and Applied Mathematics. 2022;(2):72–87. (In Russ.) Available at: https://journals.airi.uz/index.php/pvpm/article/view/34 (accessed: 01.07.2025).

9. Шадманов И.У., Шадманова К.У., Фатуллаева М.Ш. Многомерная математическая модель и численный алгоритм решения задач совместного тепловлагопереноса в неоднородных пористых тел. Проблемы вычислительной и прикладной математики. 2022;(S2):254–271. Режим доступа: https://journals.airi.uz/index.php/pvpm/article/view/71 (дата обращения: 01.07.2025).Shadmanov I.U., Shadmanova K.U., Fatullaeva M.Sh. Multidimensional mathematical model and numerical algorithm for solving problems of joint heat and moisture transfer in inhomogeneous porous bodies. Problems of Computational and Applied Mathematics. 2022;(S2):254–271. (In Russ.) Available at: https://journals.airi.uz/index.php/pvpm/article/view/71 (accessed: 01.07.2025).

10. Терлеев В.В., Нарбут М.А., Топаж А.Г., Миршель В. Моделирование гидрофизических свойств почвы как капиллярно-пористого тела и усовершенствование метода Муалема–Ван Генухтена: теория. Агрофизика. 2014;(2):35–44.Terleev V.V., Narbut M.A., Topaj A.G., Mirschel W. Modeling of hydrophysical properties of soil as a capillary-porous medium and modification of the Mualem-Van Genuchten approach: Theory. Agrophysica. 2014;(2):35–44. (In Russ.)

11. van Genuchten M.Th. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Science Society of America Journal. 1980;44(5):892–898.

12. Самарский А.А., Моисеенко Б.Д. Экономичная схема сквозного счета для многомерной задачи Стефана. Журнал вычислительной математики и математической физики. 1965;5(5):816–827.Samarskii A.A., Moiseyenko B.D. An economic continuous calculation scheme for the Stefan multidimensional problem. USSR Computational Mathematics and Mathematical Physics. 1965;5(5):43–58. https://doi.org/10.1016/0041-5553(65)90004-2

13. Лычман В.В. Численное решение задач фильтрации и влагопереноса в пористых средах [Дис. ... канд. физ.-мат. наук]. Киев; 1984. 156 с.

14. Кучеров А.Б., Николаев Е.С. Попеременно-треугольный итерационный метод решения сеточных эллиптических уравнений в произвольной области. Журнал вычислительной математики и математической физики. 1977;7(3):664–675.Kucherov A.B., Nikolaev E.S. An alternately triangular iterative method for solving mesh elliptic equations in an arbitrary domain. USSR Computational Mathematics and Mathematical Physics. 1977;7(3):664–675. https://doi.org/10.1016/0041-5553(77)90142-2

15. Xiong J.S. Modified upper and lower triangular splitting iterative method for a class of block two-by-two linear systems. Linear and Multilinear Algebra. 2021;71(1):29–40. https://doi.org/10.1080/03081087.2021.2017833

16. Gregoire M. Professional C++. 5th еd. –Birmingham: Wrox; 2021. 1312 р.

17. Stroustrup B. A Tour of C++. 3rd ed. Reading: Addison-Wesley Professional; 2022. 320 p.