Разработка имитационной модели динамики карьерного автосамосвала для определения нагрузок, действующих на несущую систему и грузовую платформу при загрузке и разгрузке дисперсного груза

Д.М. Дубинкин¹, И.В. Чичекин², Я.Ю. Левенков², Г.А. Арутюнян^2
1 Кузбасский государственный технический университет им. Т.Ф. Горбачева, г. Кемерово, Российская Федерация
² Московский государственный технический университет им. Н.Э. Баумана, г. Москва, Российская Федерация
Горная Промышленность №6 / 2021 стр. 117-126

Резюме: Для карьерных автосамосвалов важно минимизировать массу несущей системы и грузовой платформы при достаточном уровне ее жесткости и прочности. Это требование существенно влияет на массу перевозимого груза, себестоимость перевозок и, в конечном итоге, на экономическую эффективность работ по добыче полезных ископаемых. Процессы загрузки и разгрузки сыпучих грузов, которые перевозят карьерные автосамосвалы, оказывают большое влияние на долговечность несущей системы. Поэтому правильный учет динамики дисперсного груза является важной и актуальной задачей. Современные системы по расчету динамики твердых тел позволяют проводить совместное моделирование с приложениями по расчету динамики дисперсных тел. Такой подход позволяет получить адекватные нагрузки в шарнирах и силовых связях модели, произвести анализ нагружения грузовой платформы, проанализировать долговечность элементов карьерного самосвала, определить геометрию грузовой платформы. Для проведения моделирования необходимо разработать математическую модель карьерного самосвала, включающую все основные элементы и подсистемы, модель дисперсного груза, модель грузовой платформы. Цель исследования – разработка математической модели карьерного самосвала для определения нагрузок в шарнирах и силовых связях, связанных с несущей системой и грузовой платформой, для прочностных расчетов и анализа долговечности. Расчеты произведены при совместном использовании системы расчета динамики твердых тел и приложений по расчету динамики дисперсных тел.

Ключевые слова: карьерный самосвал, несущая система, грузовая платформа, динамика твердых тел, динамика дисперсных тел, долговечность, нагрузки, расчет на прочность, метод конечных элементов

Благодарности: Работа выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации в рамках соглашения № 075-11-2020-031 от 14.12.2020 г. с ПАО «КАМАЗ» по комплексному проекту «Создание высокотехнологичного производства семейства роботизированных карьерных самосвалов грузоподъемностью до 90 т с электромеханической трансмиссией на основе цифровых технологий», при участии ФГБОУ ВО «Кузбасский государственный технический университет имени Т.Ф. Горбачева» в части выполнения научно-исследовательских, опытно-конструкторских и технологических работ.

Для цитирования: Дубинкин Д.М., Чичекин И.В., Левенков Я.Ю., Арутюнян Г.А. Разработка имитационной модели динамики карьерного автосамосвала для определения нагрузок, действующих на несущую систему и грузовую платформу при загрузке и разгрузке дисперсного груза. Горная промышленность. 2021;(6):117–126. DOI: 10.30686/1609-9192-2021-6-117-126.

Информация о статье

Поступила в редакцию: 12.11.2021

Поступила после рецензирования: 30.11.2021

Принята к публикации: 02.12.2021

Информация об авторах

Дубинкин Дмитрий Михайлович – кандидат технических наук, доцент, доцент кафедры металлорежущих станков и инструментов, Кузбасский государственный технический университет им. Т.Ф. Горбачева, г. Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Чичекин Илья Викторович – кандидат технических наук, доцент, доцент кафедры колесных машин, Московский государственный технический университет им. Н.Э. Баумана, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript., Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Левенков Ярослав Юрьевич – кандидат технических наук, доцент, доцент кафедры колесных машин, Московский государственный технический университет им. Н.Э. Баумана, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Арутюнян Георгий Артурович – кандидат технических наук, старший преподаватель кафедры колесных машин, Московский государственный технический университет им. Н.Э. Баумана, г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

Транспортировка сыпучих грузов и полезных ископаемых в открытых карьерах производится как в нашей стране, так и за рубежом, в основном автомобильным транспортом [1–8].

Процессы погрузки и разгрузки для карьерных автосамосвалов существенно влияют на ресурс несущей системы и грузовой платформы. Процесс загрузки автосамосвала связан с постепенным увеличением нагрузки, действующей на элементы несущей системы. Также возможно возникновение скачков нагрузки, связанных с процессами высыпания груза: неоднородность геометрических характеристик элементов груза, слипание груза, прилипание груза к ковшу погрузчика и т.д. Разгрузка, помимо изменения силовых факторов за счет высыпания груза и изменения его центра масс за счет подъема платформы гидроцилиндрами, также характеризуется перераспределением нагрузки между элементами несущей системы и грузовой платформы. Данные нагрузочные режимы являются циклическими, которые сопровождают весь период эксплуатации самосвала. Величина изменения этих нагрузок значительная, т.к. грузоподъемность карьерного самосвала сопоставима с его снаряженной массой. Поэтому для прогнозирования усталостной долговечности несущей системы и грузовой платформы необходимо учитывать режимы погрузки и разгрузки.

Аналитические расчеты на прочность грузовых платформ выполняют как для статически определимых систем, учитывают статическую распределённую нагрузку от груза, которая моделируется как гидростатическое давление, приложенное к стенкам и реакциям в узлах, хотя лонжероны грузовой платформы расположены на опорах, находящихся на лонжеронах несущей системы, что приводит к статической неопределимости. Поэтому целесообразно для определения нагрузок использовать твердотельные динамические модели карьерных автосамосвалов, которые позволят определить нагрузки для всех эксплуатационных режимов, в том числе и для процессов погрузки и разгрузки.

Целью работы является разработка математической модели карьерного самосвала для определения нагрузок в шарнирах и силовых связях, связанных с несущей системой и грузовой платформой, для прочностных расчетов и анализа долговечности.

Для достижения цели в работе представлена имитационная модель динамики карьерного автосамосвала, грузовой платформы и описана модель дисперсного груза. Расчеты произведены при совместном использовании системы расчета динамики твердых тел и приложений по расчету динамики дисперсных тел. Представлены результаты расчета.

Описание динамической модели карьерного автосамосвала

Общий вид динамической модели карьерного автосамосвала, разработанной в системе расчета динамики тел, представлен на рис.1. Показаны положение центра масс и снаряженная масса модели.

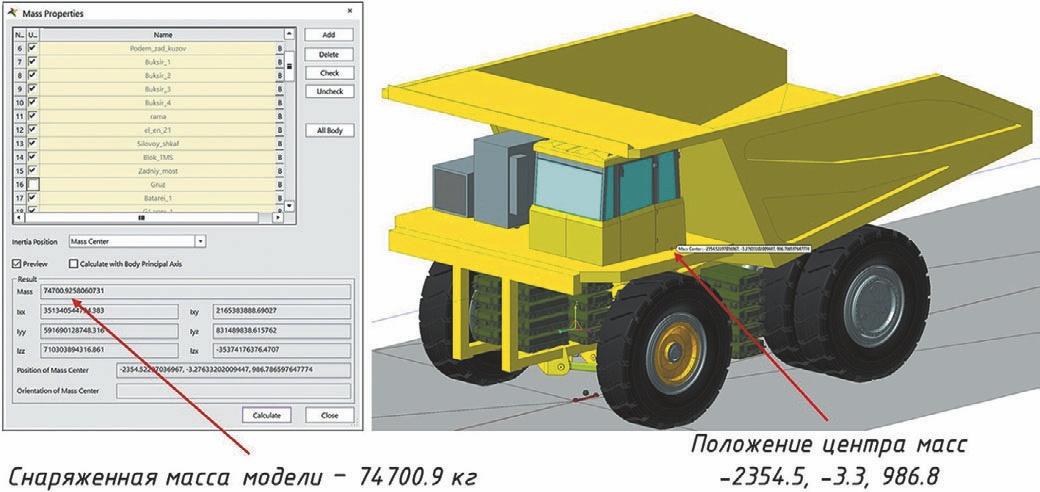
Рис. 1 Общий вид модели карьерного автосамосвала и положение центра масс в снаряженном состоянии

Fig. 1 General view of the dump truck model and position of the center of mass in the loaded state)

Математическая модель автосамосвала (рис. 2) включает в себя батареи, груз, грузовую платформу (грузонесущую ёмкость), задний мост с подвеской, кабину, колеса, несущую систему (раму), опорную поверхность (дорогу), передний мост с подвеской и рулевым управлением, ТЭД привода ведущих колес.

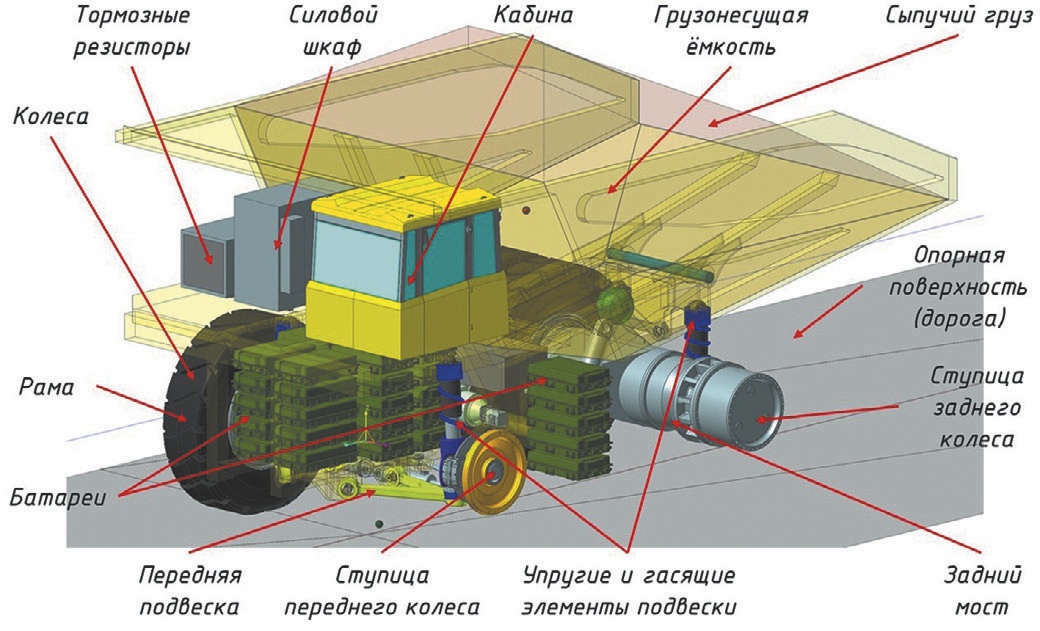
Рис. 2 Компоненты математической модели карьерного автосамосвала

Fig. 2 Components of the dump truck mathematical model

Допущения, использованные при построении модели:

‒ все звенья динамической системы абсолютно жесткие;

‒ трение в шарнирах отсутствует;

‒ деформация колес учтена в модели взаимодействия колеса с опорной поверхностью, силы на колесо приложены в центре колеса.

Имитационные модели, созданные в приложениях по расчету динамики твердых тел, позволяют определять нагрузки в шарнирах для последующих прочностных расчетов [7–14], определять нагрузки для расчета долговечности деталей [15–20], подбирать компоненты колесной машины.

Общий вид системы подрессоривания карьерного автосамосвала представлен на рис. 3. Передняя подвеска – независимая с одним поперечным рычагом. Задняя подвеска – зависимая с шаровым шарниром крепления балки моста к раме и одной поперечной тягой. Упругий и гасящий элементы передней и задней подвесок заданы силовым соединением типа «Пружина» в программном комплексе по расчету динамики твердых тел (рис. 3).

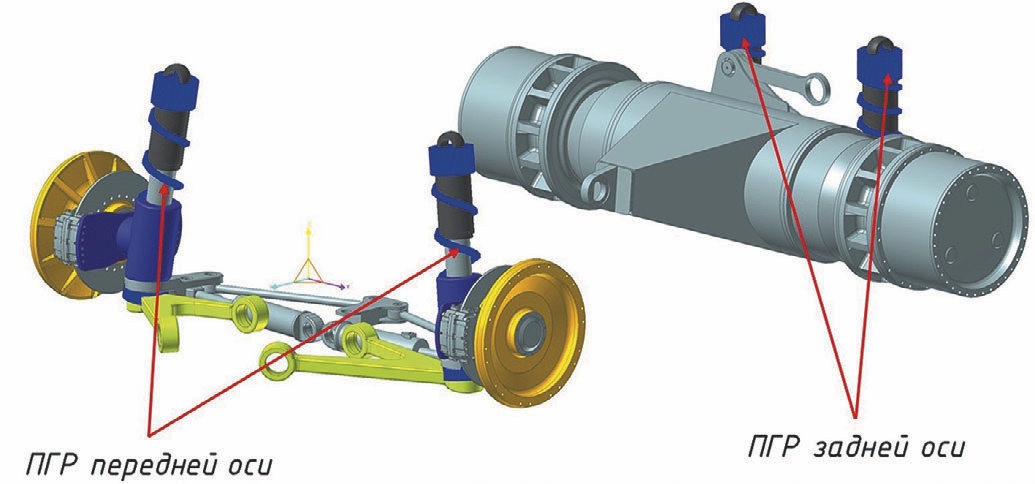
Рис. 3 Размещение упругих элементов подвески

Fig. 3 Location of the suspension elastic elements

Грузонесущая емкость опирается на лонжероны рамы в 20 точках (по 10 опор на каждой стороне). Задняя опора соединена с рамой через ось опрокидывания шарниром вращения revolute (рис. 4).

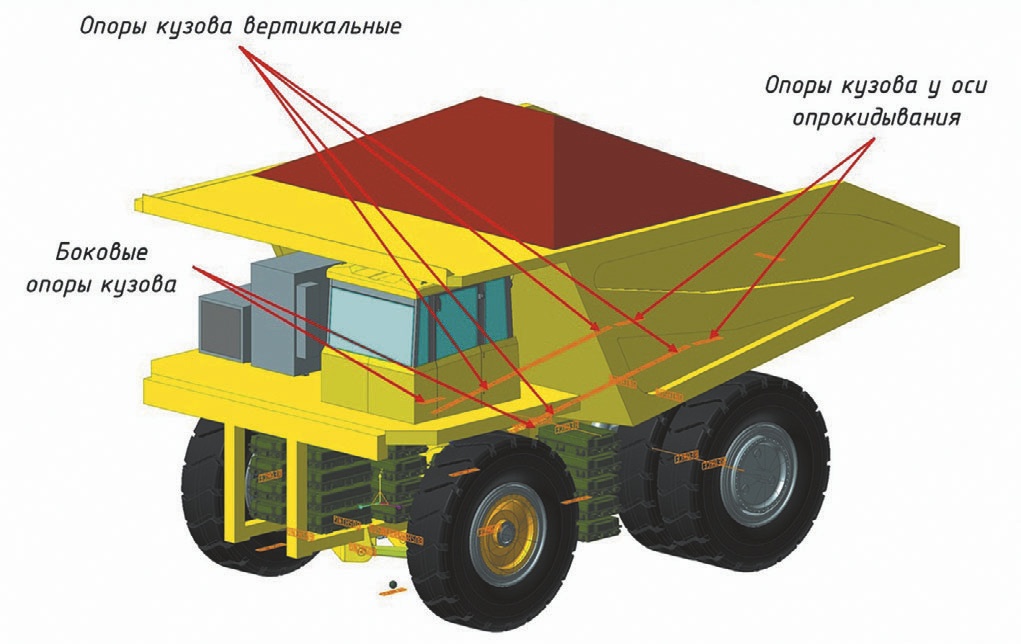
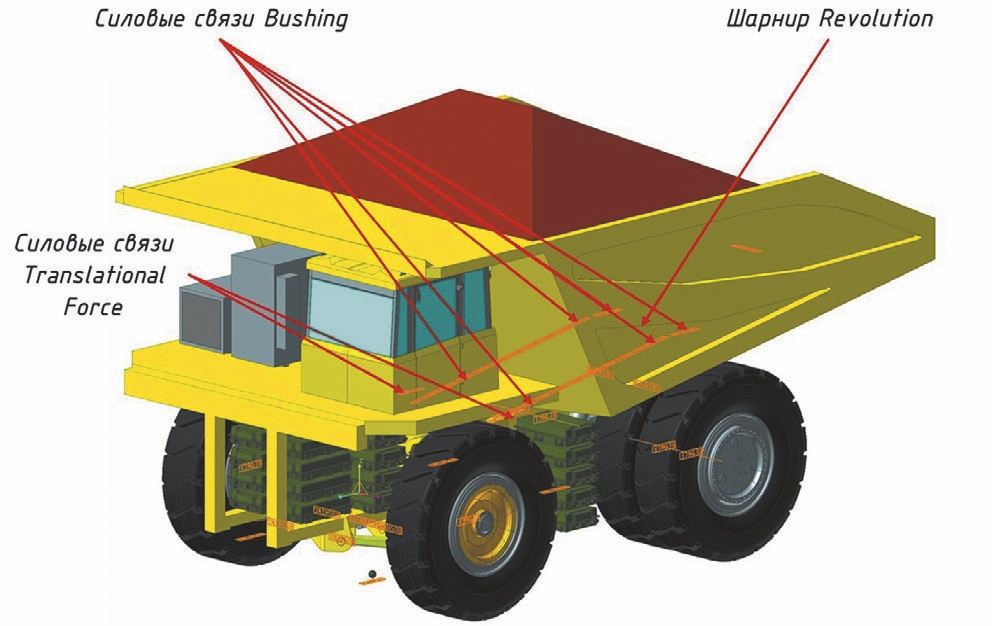
Рис. 4 Шарниры модели грузонесущей емкости роботизированного карьерного самосвала

Fig. 4 Pivot points of the robotic dump truck load box model

Опоры могут воспринимать только нагрузки, нормальные к плоскости лонжерона рамы. Также в модель добавлены два силовых элемента (Translational Force), воспринимающих боковые нагрузки. Для определения нагрузок от сыпучего груза реальная CAD модель грузонесущей емкости заменяется на упрощенную поверхностную модель, представленную на рис. 5.

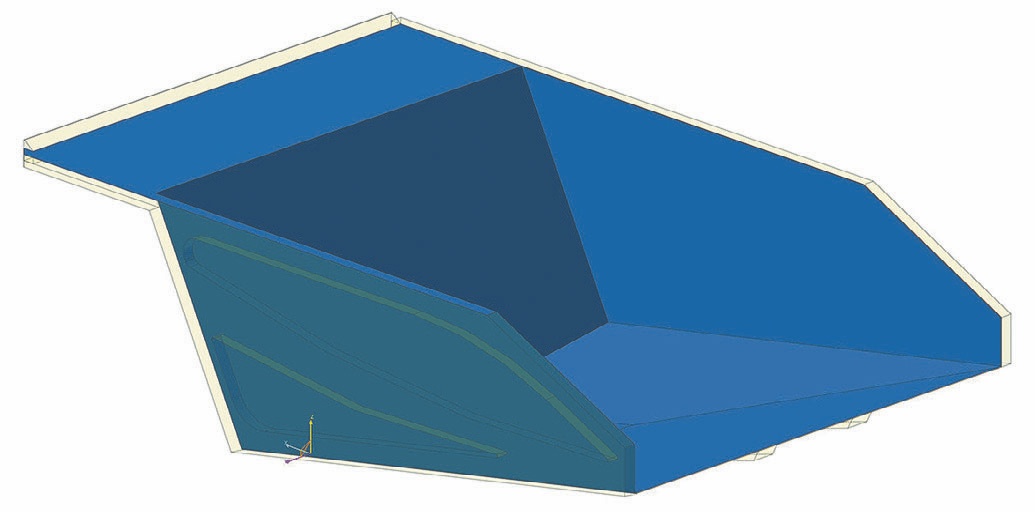
Рис. 5 Поверхность взаимодействия дискретного груза

Fig. 5 Interaction surface of a bulk load

Моделирование сыпучего груза

Сыпучий груз смоделирован в подключаемом приложении расчета динамики дискретных тел. Форма груза задана в виде четырех сфер, образующих тело, похожее на тетраэдр (рис. 6).

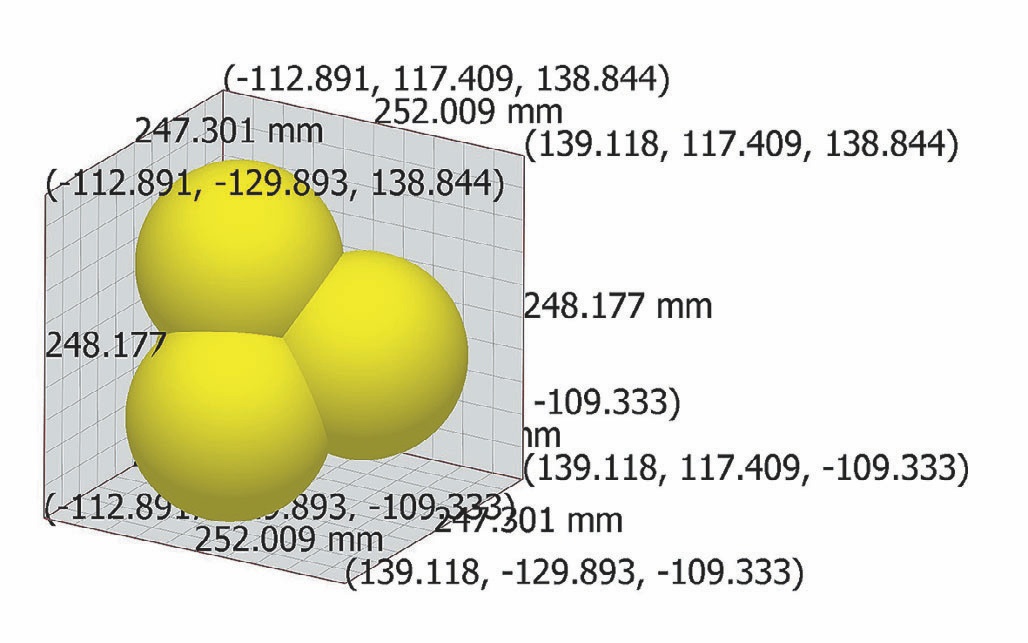
Рис. 6 Общий вид модели частички грунта с основными размерами

Fig. 6 General view of a rock particle model with basic dimensions

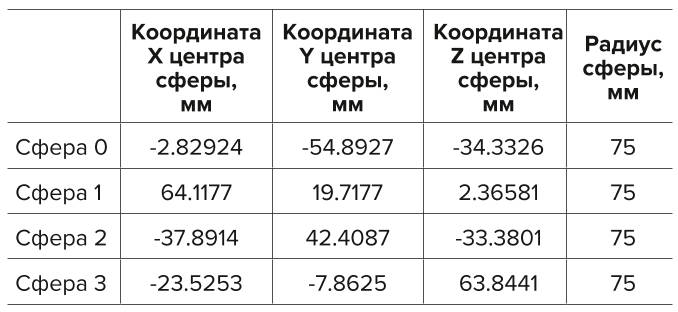
Основные размеры модели груза представлены в табл. 1. Плотность груза задана равной 1700 кг/м³. Масса одной частицы груза с номинальным радиусом 75 мм – 10.3431 кг, объем – 0.00608417 м³. Для учета случайного размера частичек реального груза размеры сфер случайно изменяются в диапазоне 0.75…1.25R.

Таблица 1 Координаты центра сфер модели груза

Table 1 Coordinates of… the load model circumcenter

Для расчета максимальных нагрузок общая масса груза взята на 10% больше номинальной и составила 99000 кг. Сыпучий груз высыпается из геометрического тела, смоделированного в виде куба с размерами грани 2154 мм и центром с координатами -3500, 0, 7500, – моделирующего ковш экскаватора (рис. 7).

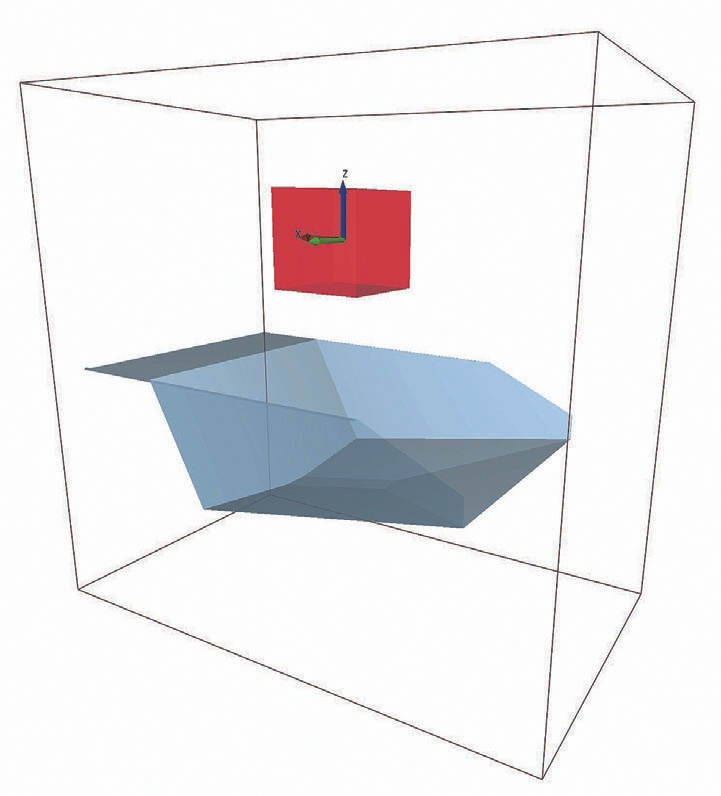
Рис. 7 Общий вид модели грузонесущей емкости и модели ковша

Fig. 7 General view of the load box and bucket models

Груз высыпается неравномерно по закону, представленному зависимостью:

M(time) = 13.428 · ((1 ‒ cos(2π·time/12))¹⁰), где time – время моделирования.

Для возможности контроля массы дисперсных тел, находящихся в кузове, в модель добавлен массовый сенсор, представляющий из себя параллепипед заданного объема, позволяющий определить массу дисперсных тел, находящихся внутри заданного объема. Общий вид грузонесущей емкости и сенсора представлен на рис. 8.

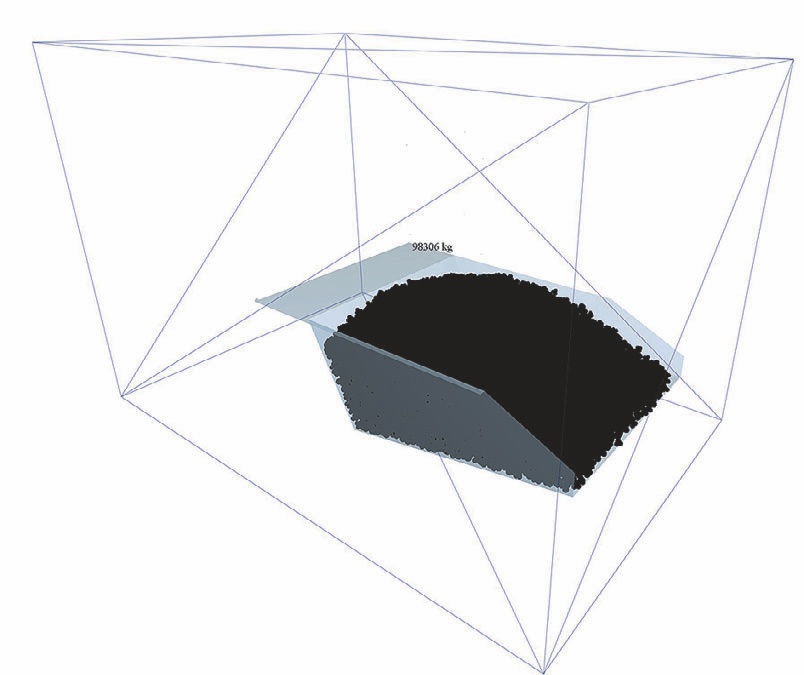
Рис. 8 Общий вид грузонесущей емкости и массового сенсора

Fig. 8 General view of the load box and the weight sensor

Нагрузки на грузонесущую емкость действуют с одной стороны – с шасси карьерного автосамосвала в шарнирах и силовых связях, с другой – со стороны дисперсного тела. Нагрузки в шарнирах получены в приложении по расчету динамики твердых тел, нагрузки от действия дисперсных тел – в модуле расчёта динамики дисперсных тел.

Описание расчетного случая

Общее время моделирования составило 90 с, из них первые 40 с происходит загрузка в карьерный автосамосвал, затем с 55-й по 90-ю – подъем грузовой платформы и высыпание груза. Изменение высоты подъема грузовой платформы осуществлялось с помощью кинематического изменения положения звеньев, моделирующих силовые гидроцилиндры подъема грузовой платформы.

Рис. 9 Общий вид модели с шарнирами и силовыми связями левого и правого ГЦ грузовой платформы карьерного автосамосвала

Fig. 9 General view of the model with pivot points and force links of the left and right hydraulic cylinder of the dump truck load platform

Усилие в шарнирах получалось автоматически, так чтобы выполнялся загнанный закон изменения положения. Модель каждого ГЦ состоит из 2 секций, связанных между собой шарнирами, разрешающими перемещение только вдоль оси ГЦ (рис. 9). Максимальный ход ГЦ составляет 1750 мм (рис. 10). С грузовой платформой ГЦ соединен шаровыми шарнирами, с рамой – силовыми связями (Bushing).

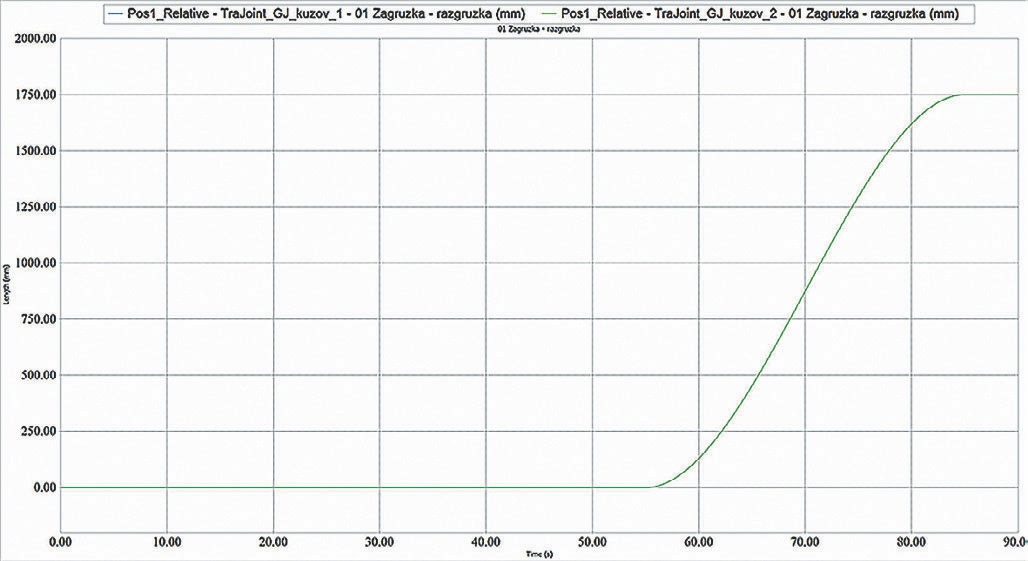
Рис. 10 График изменения хода шарнира ГЦ грузовой платформы карьерного автосамосвала

Fig. 10 Variation chart of the hydraulic cylinder pivot movement of the mining dump truck load platform

Описание результатов моделирования

На рис. 11 представлен график изменения массы груза в грузонесущей емкости во время моделирования загрузки в карьерный автосамосвал. Изменение нормальных нагрузок в пятне контакта колес с опорной поверхностью представлено на рис. 12. При моделировании колеса передней оси заторможены, карьерный автосамосвал при загрузке не изменяет своего положения.

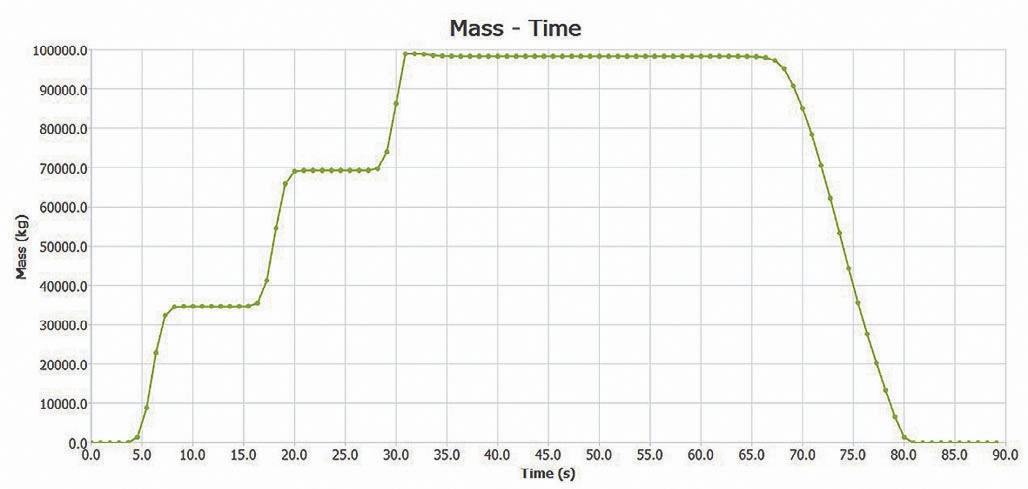
Рис. 11 График изменения массы груза в грузонесущей емкости во время моделирования

Fig. 11 Variation chart of the load weight inside the dump box during the simulation

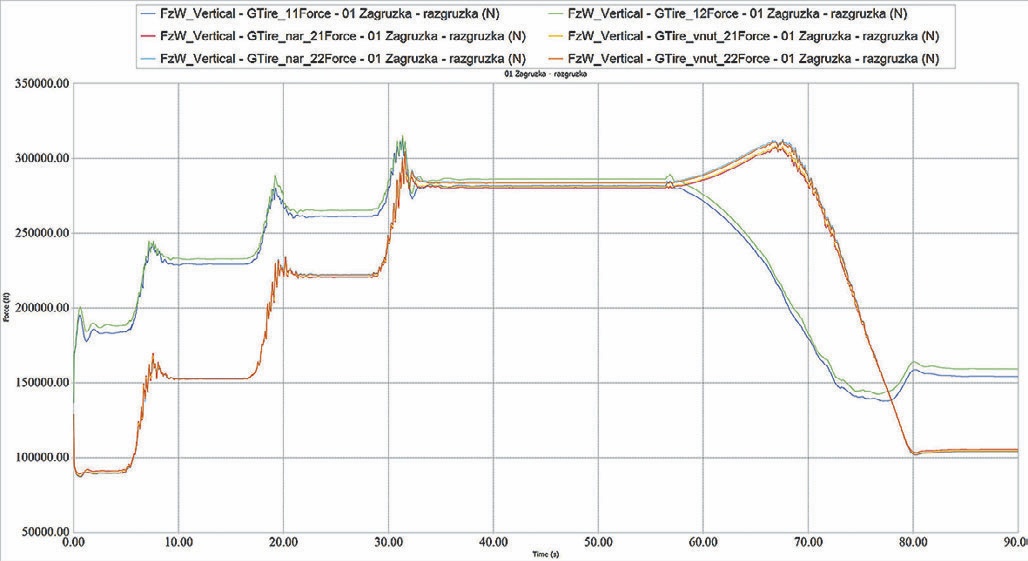
Рис. 12 График изменения нормальных реакций между колесами карьерного автосамосвала и опорной поверхностью

Fig. 12 Variation chart of normal reactions between the dump truck wheels and the bearing surface

Усилия от дисперсного груза передаются в приложение по расчету динамики твердых тел. Графики изменения сил и моментов во время моделирования представлены на рис. 13.

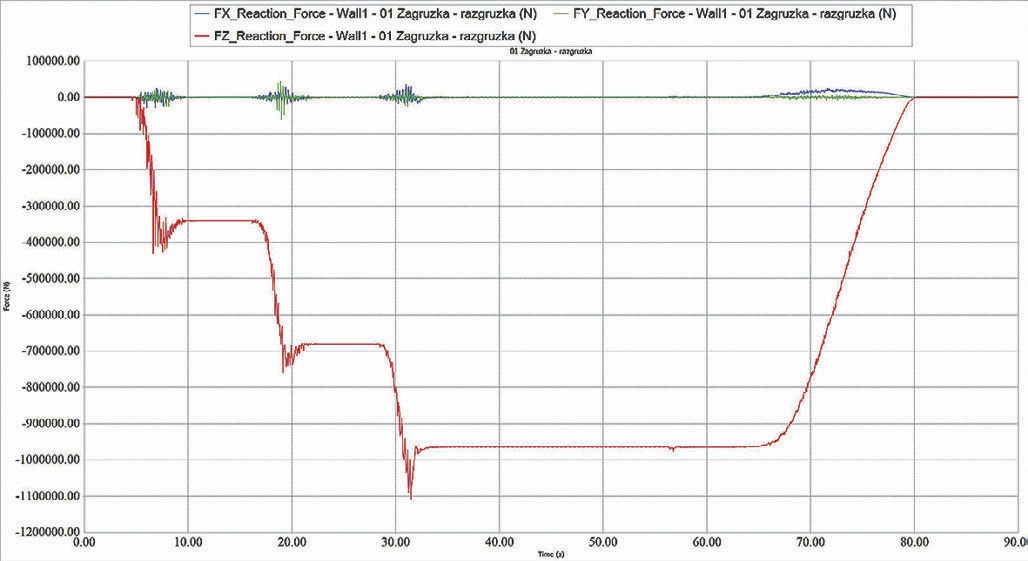
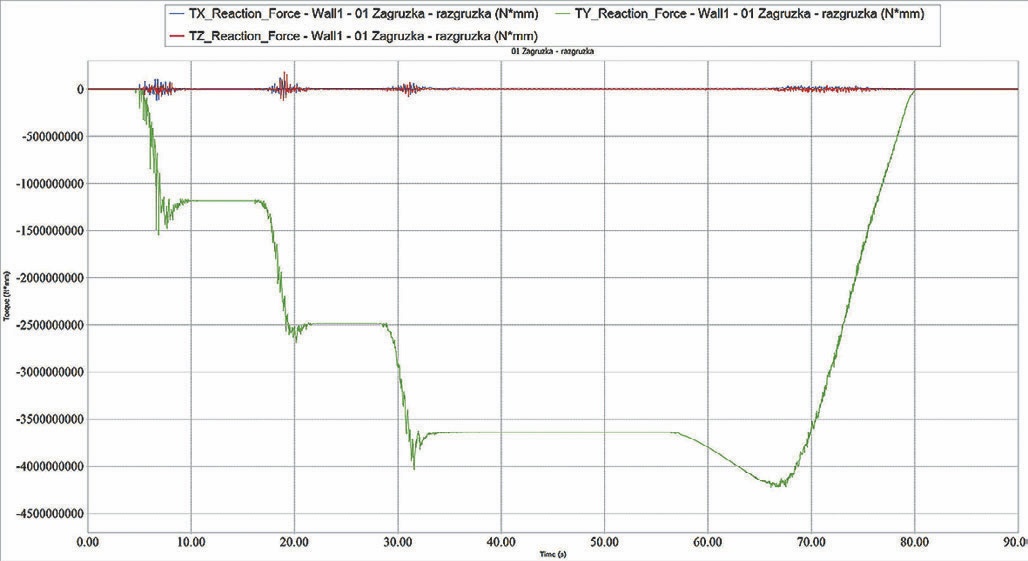
Рис. 13 График суммарных сил и моментов, передаваемых от дисперсного груза в приложение по расчету динамики твердых тел в проекции ГСК

Fig. 13 Chart of total forces and moments transmitted from the dispersed load to the application for calculation of dynamics of solids in the GSK projection

Усилия, развиваемые ГЦ подъёма грузовой платформы, представлены на рис. 14.

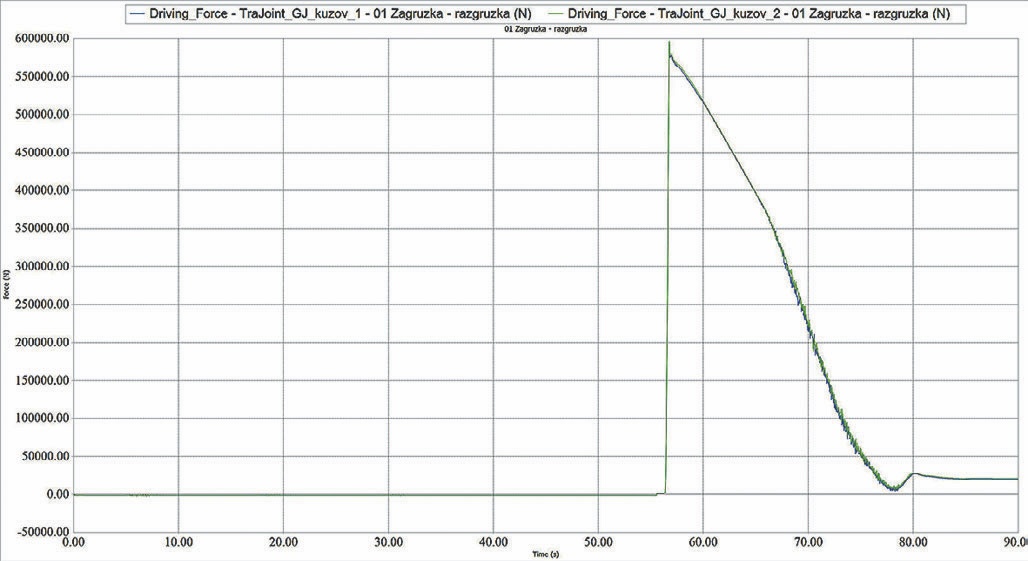
Рис. 14 График усилий, развиваемых ГЦ карьерного автосамосвала

Fig. 14 Chart of forces developed by hydraulic cylinders of the dump truck

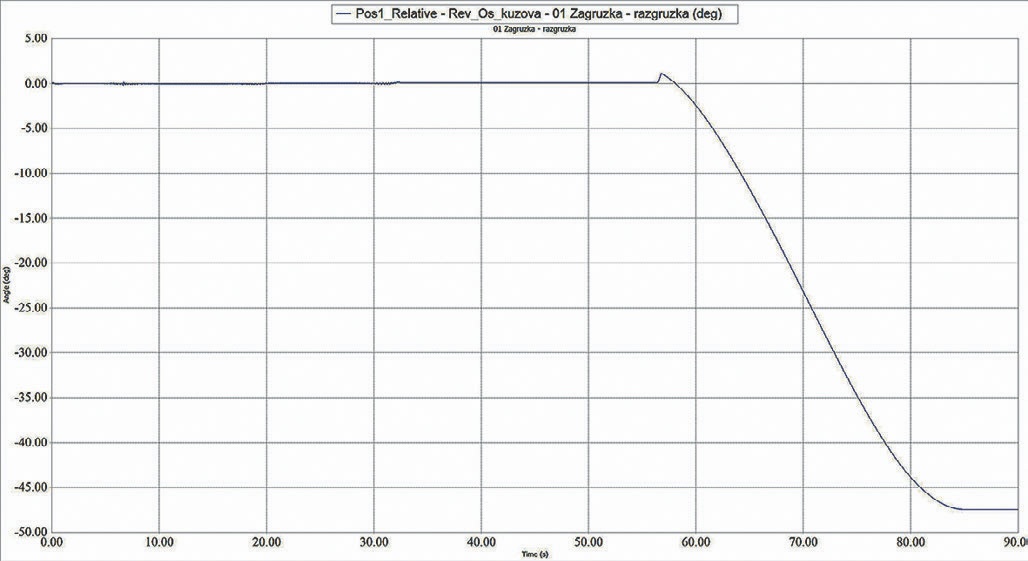
Рис. 15 График изменения угла опрокидывания карьерного автосамосвала во время моделирования

Fig. 15 Chart of the dump truck tilting angle change during the simulation

Кинограмма с анимацией моделирования представлена ниже (рис. 16). На рисунках показано положение дисперсного груза и положение карьерного автосамосвала. Для примера ниже приведены нагрузки на грузонесущую емкость, полученные для полной загрузки карьерного автосамосвала (время моделирования 50 с).

Рис. 16 Кинограмма с анимацией моделирования загрузки-разгрузки карьерного автосамосвала

Fig. 16 Stage-wise animation of simulating loading and dumping of the mine dump truck

Общий вид распределения нагрузок по поверхности грузонесущей емкости при полной загрузке карьерного автосамосвала показан на рис. 17. Для наглядности груз не показан. Наибольшее значение силы, равное 2738.58 Н, получено на передней стенке грузонесущей емкости. На рисунке также показаны векторы сил и моментов реакций в пятне контакта и усилия в опорах грузовой платформы.

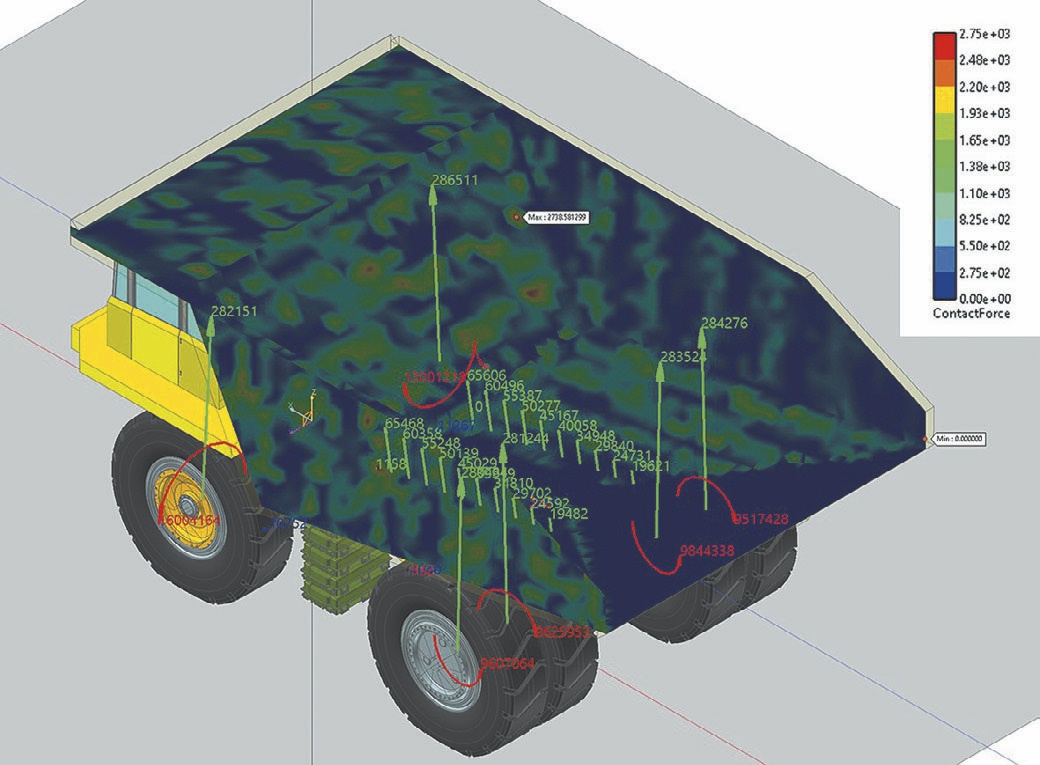
Рис. 17 Общий вид распределения контактных сил по поверхности грузонесущей емкости

Fig. 17 General view of the contact forces distribution over the dump box surface

Выводы

В работе получена имитационная модель динамики карьерного автосамосвала для получения нагрузок, действующих на несущую систему и грузовую платформу при погрузке и разгрузке.

Разработанная модель динамики автосамосвала универсальная, она позволяет не только определять нагрузки в шарнирах и силовых связях, но и анализировать кинематику подвески, кинематику механизма поворота, работу гидроцилиндров механизма опрокидывания грузонесущей емкости, проводить анализ эксплуатационных свойств.

По полученным результатам моделирования возможно провести комплексную оценку работоспособности несущей системы и грузовой платформы как от усилий со стороны силовых факторов, так и от распределённой нагрузки от дисперсного груза.

Список литературы

1. Kartashov A., Kositsyn B., Kotiev G., Nazarenko S., Dubinkin D. Ensuring energy efficiency and safety of the cyclic operation of the mining dump truck. E3S Web of Conferences. 2020;174:03009. https://doi.org/10.1051/e3sconf/202017403009

2. Дубинкин Д.М. Обоснование необходимости создания тяжелых платформ для открытых горных работ. Горное оборудование и электромеханика. 2020;(4):59–64. https://doi.org/10.26730/1816-4528-2020-4-59-64

3. Костюк С.Г., Чичекин И.В., Федосенков Б.А., Дубинкин Д.М. Мониторинг динамического состояния автономных тяжелых платформ на карьерных маршрутах горнорудных предприятий. Устойчивое развитие горных технологий. 2020;12(4):600–608. (In Russ.) https://doi.org/10.21177/1998-4502-2020-12-4-600-608

4. Дубинкин Д.М., Аксенов В.В., Тюленев М.А., Марков С.О. Влияние горнотехнических факторов на производительность беспилотных карьерных автосамосвалов. Техника и технология горного дела. 2020;(4):42–69. https://doi.org/10.26730/2618-7434-2020-4-42-69

5. Дубинкин Д.М., Карташов А.Б., Арутюнян Г.А., Бузунов Н.В., Сорокин К.П., Ялышев А.В. Современное состояние техники и технологий в области карьерных самосвалов с накопителями энергии. Горное оборудование и электромеханика. 2020;(6):31–42. https://doi.org/10.26730/1816-4528-2020-6-31-42

6. Тарасов П.И. Особенности создания и применения на открытых горных работах специализированных транспортных средств. Горный информационно-аналитический бюллетень. 2008;(8):39–51.

7. Kartashov A., Harutyunyan G., Kosolapov A., Shkarupelov E. Justification of the concept of creating a perspective dump truck. IOP Conference Series: Materials Science and Engineering. 2020;779:012028. https://doi.org/10.1088/1757-899X/779/1/012028

8. Vdovin D., Chichekin I., Ryakhovsky O. Quad bike frame dynamic load evaluation using full vehicle simulation model. IOP Conference Series: Materials Science and Engineering. 2019:589:012025. https://doi.org/10.1088/1757-899X/589/1/012025

9. Vdovin D.S., Chichekin I.V., Levenkov Y.Y., Shabolin M.L. Automation of wheeled vehicles load bearing frames finite-element models loading procedure by using inertia relief method and vehicle multi-body dynamics model. IOP Conference Series: Materials Science and Engineering. 2019;534:012024. https://doi.org/10.1088/1757-899x/534/1/012024

10. Полунгян А.А. (ред.). Проектирование полноприводных колесных машин. М.: Изд-во МГТУ им. Н.Э. Баумана; 2008.

11. Kotiev G.O., Padalkin B.V., Kartashov A.B., Dyakov A.S. Designs and development of russian scientific schools in the field of crosscountry ground vehicles building. ARPN Journal of Engineering and Applied Sciences. 2017;12(4):1064-1071. https://arpnjournals.org/jeas/research_papers/rp_2017/jeas_0217_5726.pdf

12. Вдовин Д.С. Расчет нагрузок на звенья независимой подвески ходовой части автомобиля 8х8 с использованием Nx Motion. В кн.: Будущее автомобилестроения в России: материалы 85-й междунар. науч.-техн. конф., г. Москва, 24 апреля 2014 г. М.; 2014. С. 2–6.

13. Gorelov V.A., Komissarov A.I. Mathematical model of the straight-line rolling tire – rigid terrain irregularities interaction. Procedia Engineering. 2016;150:1322–1328. https://doi.org/10.1016/J.PROENG.2016.07.309

14. Вдовин Д.С., Чичекин И.В., Поздняков Т.Д. Виртуальный стенд для определения нагрузок на рулевое управление автомобиля. Инженерный журнал: наука и инновации. 2017;(8):3. https://doi.org/10.18698/2308-6033-2017-8-1642

15. Vdovin D., Chichekin I. Loads and stress analysis cycle automation in the automotive suspension development process. Procedia Engineering. 2016;150:1276–1279. https://doi.org/10.1016/J.PROENG.2016.07.285

16. Вдовин Д.С., Левенков Я.Ю., Чичекин И.В. Нагружение конечно-элементных моделей несущих систем колесных машин с применением метода inertia relief и твердотельной динамической модели автомобиля. В кн.: Технологии и компоненты интеллектуальных транспортных систем: материалы Международного автомобильного научного форума (МАНФ-2018), г. Москва, 18–19 октября 2018 г. М.: НАМИ; 2018. С. 620–640.

17. Вдовин Д.С., Чичекин И.В., Левенков Я.Ю. Прогнозирование усталостной долговечности элементов подвески полуприцепа на ранних стадиях проектирования. Труды НАМИ. 2019;(2):14–23.

18. Чичекин И.В., Максимов Р.О. Моделирование работы автомобильного дифференциала в системе расчёта динамики твёрдых тел. Известия Московского государственного технического университета МАМИ. 2019;(2):80–87. https://doi.org/10.31992/2074-0530-2019-40-2-80-87

19. Pacejka H.B. Tyre and vehicle dynamics. Oxford, Butterworth Heinemann; 2006. 672 p.

20. Pacejka H.B., Besselink I.Y. Magic formula tyre model with transient properties. Vehicle System Dynamics. 1997;27(Suppl. 1):234–249. https://doi.org/10.1080/00423119708969658