Разработка численных геомеханических моделей с различной степенью детализации на примере шахты «Ангидрит» рудника «Кайерканский»
![]() Ю.Ю. Головченко1 , И.С. Лепехин2, А.Е. Румянцев1, М.А. Соннов3, А.В. Трофимов1
Ю.Ю. Головченко1 , И.С. Лепехин2, А.Е. Румянцев1, М.А. Соннов3, А.В. Трофимов1
1 ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация
2 ООО «Норильский обеспечивающий комплекс», г. Норильск, Российская Федерация
3 ООО «Фидесис», г. Москва, Российская Федерация
Горная Промышленность №3 / 2023 стр. 79-88
Резюме: Ввиду осложнения условий ведения горных работ одним из наиболее перспективных направлений становится численное моделирование, которое позволяет получить данные для разработки эффективных технологических решений. Однако создание качественных численных моделей является крайне трудоемкой и наукоемкой задачей. Оптимизация процесса численного моделирования является крайне актуальной на текущий момент. Использование глобальных численных моделей с высокой детализацией позволяет не только укрупненно оценить напряженно-деформированное состояние скального массива на значительной площади, но и качественно оценить некоторые локальные эффекты. Такие модели позволяют более корректно выбрать наиболее опасные участки для построения локальных расчетных схем. Ввиду высокой детализации моделируемого подземного сооружения глобальная численная модель может выступать в роли «донора» исходной геометрии для локальных расчетных схем, а экспортированный тензор напряжений – в качестве граничных условий, что повысит точность локального численного моделирования. Благодаря такому подходу к численному моделированию возможно существенно повысить его качество. Несмотря на то что детализированные глобальные численные модели могут отображать некоторые локальные феномены поведения массива, не стоит воспринимать их как панацею. Результаты, полученные в глобальной численной модели, являются достаточно укрупненными и в случае локальных задач лишь указывают на наличие того или иного явления в определенной зоне, однако не могут количественно описать его. Исходя из этого переход от глобальных численных моделей к локальным является необходимой частью работы. В данной работе приведен пример полного цикла создания связки из детализированной глобальной и локальной численных моделей. Цикл включает в себя все этапы разработки: от оптимизации исходной геометрии до выполнения пошагового расчета и анализа полученных результатов. Благодаря использованному подходу удалось добиться как качественной, так и количественной сходимости с результатами натурных наблюдений.
Ключевые слова: горные работы, горные породы, численное моделирование, численная геомеханическая модель, численная модель подземного сооружения, целики, камерно-целиковая система отработки
Для цитирования: Головченко Ю.Ю., Лепехин И.С., Румянцев А.Е., Соннов М.А., Трофимов А.В. Разработка численных геомеханических моделей с различной степенью детализации на примере шахты «Ангидрит» рудника «Кайерканский». Горная промышленность. 2023;(4):79–88. https://doi.org/10.30686/1609-9192-2023-4-79-88
Информация о статье
Поступила в редакцию: 18.06.2023
Поступила после рецензирования: 12.07.2023
Принята к публикации: 13.07.2023
Информация об авторах
Головченко Юрий Юрьевич – научный сотрудник лаборатории геотехники, ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация; ORCID: https://orcid.org/0000-0003-2980-2173; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Лепехин Илья Сергеевич – заместитель директора рудника по горным работам, ООО «Норильский обеспечивающий комплекс», г. Норильск, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Румянцев Александр Евгеньевич – кандидат технических наук, главный специалист лаборатории геотехники, ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация; https://orcid.org/0000-0002-2204-961X; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Соннов Максим Александрович – действительный член Академии горных наук, заместитель генерального директора по продажам, ООО «Фидесис», г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Трофимов Андрей Викторович – кандидат технических наук, заведующий лабораторией геотехники, ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация; https://orcid.org/0000-0001-7557-9801; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Введение
В настоящее время в условиях осложнения горно-геологических и горнотехнических условий разрабатываемых месторождений для поддержания темпов производства имеется необходимость как в создании эффективных технологических решений [1–3], так и в качественном прогнозе состояния и поведения массива горных пород в процессе его отработки [4–6].
Принимая во внимание подземную разработку месторождений, следует отметить, что проведение качественного прогноза состояния массива горных пород требует значительного объема инструментальных исследований. Так, например, для определения напряженно-деформированного состояния в массиве необходимо производить трудоемкие и дорогостоящие измерения в нескольких точках рудного поля. Однако при данном способе можно определить поле напряжений только в настоящий момент времени. Произвести качественный прогноз во времени, с учетом ведения горных работ, можно только при помощи численного моделирования.
В последние несколько десятилетий ввиду значительно возросших вычислительных мощностей численные методы нашли свое широкое применение. В широком смысле численные методы можно классифицировать как связные и несвязные (дискретные) [7]. Существует достаточно большое количество различных методов для оценки расчетов в геомеханике. Наиболее важными или, по крайней мере, наиболее часто используемыми методами являются: для связных моделей – метод конечных разностей (МКР), метод конечных элементов (МКЭ) и метод граничных элементов (МГЭ); для дискретных – метод дискретных элементов (МДЭ), дискретный деформационный анализ (ДДА) и модель связных частиц (БПМ) [8].
Метод конечных элементов (МКЭ) зарекомендовал себя как надежный и доступный инструмент для осуществления моделирования задач геомеханики [9; 10]. Однако для выполнения качественного расчета необходимо иметь достаточно достоверные исходные данные, которые можно получить только в результате: испытаний на определение физико-механических свойств горных пород; полевого картирования горных выработок для оценки нарушенности; проведенных лабораторных исследований [11–14].
Применение МКЭ для геомеханических расчетов имеет широкое распространение как в горном деле, так и в гражданском строительстве [10; 15; 16].
Разработка глобальных численных моделей подземных сооружений с высокой степенью детализации является достаточно перспективным направлением в геомеханике. Использование подобных моделей позволяет получить не только укрупненные данные о напряженно-деформированном состоянии (НДС) массива, но и уточнить значения НДС на конкретных интересующих участках, что может быть использовано в дальнейшем при решении локальных задач.
В данной статье рассмотрена возможность применения программного продукта CAE Fidesys при численном моделировании глобальной и локальной геомеханических моделей шахты «Ангидрит» рудника «Кайерканский» с целью рассмотрения устойчивости междукамерных целиков.
Создание глобальной численной модели шахты «Ангидрит»
Разработка глобальных численных моделей подземных сооружений с высокой степенью детализации является достаточно перспективным направлением в геомеханике. Использование подобных моделей позволяет получить не только укрупненное напряженно-деформированное состояние (НДС) массива, но и уточнить локальное НДС, которое может быть использовано в дальнейшем при решении локальных задач. Разработка подобных конечно-элементных моделей является важным шагом на пути к созданию цифровых двойников рудников.
Детализированная глобальная модель шахты «Ангидрит» предназначена для определения напряженно-деформированного состояния шахты в любой момент эксплуатации. Использование подобной численной модели способно не только помочь оценить развитие шахты в ретроспективе или оценить ее текущее состояние, но и оценить влияние новых работ на НДС шахты.
Для того чтобы корректно определить НДС подземного сооружения, необходимо правильно воссоздать его природное напряженно-деформированное состояние (фактически, учесть преднапряжение массива). Ввиду того что подземные работы в шахте ведутся на небольшой глубине (до 350 м), а тектонические нарушения представлены двумя вертикальными разломами на востоке и западе, не пересекающими область ведения работ, можно сделать вывод о гравитационном режиме напряжений. Таким образом, для корректного учета природного НДС достаточно учесть лишь величину горного давления от действия веса скального массива. Также на качество численной модели непосредственное влияние оказывают:
1. Учет сложной геометрии и пространственного залегания литологии;
2. Учет рельефа дневной поверхности;
3. Учет камерно-столбовой системы разработки при моделировании шахты.
Разработка численной модели шахты «Ангидрит» велась в несколько этапов. Первый этап заключался в ретопологии исходной геометрии при помощи авторского скрипта на языке программирования Python. Данный шаг является необходимым ввиду особых требований, предъявляемых к геометрии, используемой в численном моделировании.
В частности, необходимо выполнять очистку геометрии от вырожденных и узких граней, которые не только создают дополнительные концентраторы напряжений, но и существенно ухудшают качество конечно-элементной сетки. После оптимизации исходных каркасов геометрии полученные тела имеют равномерную триангуляцию. При этом потери исходной геометрии являются минимальными. Пример ретопологии каркаса приведен на рис. 1.
 Рис. 1 Оптимизация геометрии каркаса: а – до оптимизации; б – после оптимизации
Рис. 1 Оптимизация геометрии каркаса: а – до оптимизации; б – после оптимизации
Fig. 1 Optimization of the frame geometry: а) before the optimization, б) after the optimization
Второй этап заключался в сборке модели в САПР AutoCAD. Выполнялось разнесение литологических разностей по разным слоям, а также уточнение сопряжения отдельных твердых тел. Также выполнялось разделение геометрии по назначению в расчете. В частности, была сформирована камерно-целиковая система шахты в слое промышленного ангидрита. Общий вид модели в САПР AutoCAD приведен на рис. 2. Разрез по направлению Ю-С показан на рис. 3.
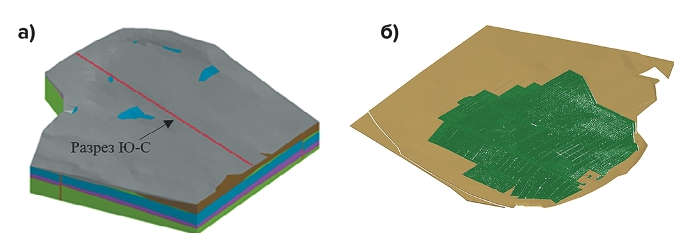 Рис. 2 Общий вид модели: а – общий вид; б – слой промышленного ангидрита с целиками и выработками
Рис. 2 Общий вид модели: а – общий вид; б – слой промышленного ангидрита с целиками и выработками
Fig. 2 General view of the model: а) general view, б) a layer of commercial anhydrite with pillars and excavations
 Рис. 3 Разрез модели по направлению Ю-С: 1 – четвертичные отложения; 2 – осадочные породы курейской свиты (мергель и аргиллит); 3 – интрузивные породы далдыканского комплекса; 4 – переслоения мергеля и ангидрита; 5 – осадочные породы зубовской свиты (мергель, ангидрит, гипс, аргиллит); 6 – ангидрит непродуктивный; 7 – мергель; 8 – продуктивный ангидрит
Рис. 3 Разрез модели по направлению Ю-С: 1 – четвертичные отложения; 2 – осадочные породы курейской свиты (мергель и аргиллит); 3 – интрузивные породы далдыканского комплекса; 4 – переслоения мергеля и ангидрита; 5 – осадочные породы зубовской свиты (мергель, ангидрит, гипс, аргиллит); 6 – ангидрит непродуктивный; 7 – мергель; 8 – продуктивный ангидрит
Fig. 3 A south-to-north cross-section of the model: 1 – Quaternary sediments, 2 – sedimentary rocks of the Kureyskaya Series (marls and mudstone), 3 – intrusive rocks of the Daldykan Complex, 4 – interbedded marls and anhydrites; 5 – sedimentary rocks of the Zubovskaya Series (marls, anhydrites, gypsum, mudstone), 6 – noncommercial anhydrites, 7 – marls, 8 – commercial anhydrites
Третий этап заключался в разбиении сетки конечных элементов. Предварительная обработка геометрии позволила не только получить конформную сетку высокого качества, но и получить возможность локального ее сгущения без понижения качества и существенного влияния на общую сетку. Конечно-элементная модель состоит из 5 243 873 тетраэдральных элементов первого порядка (899 642 узлов). Общий вид конечно-элементной сети и ее качество по критерию формы приведены на рис. 4.
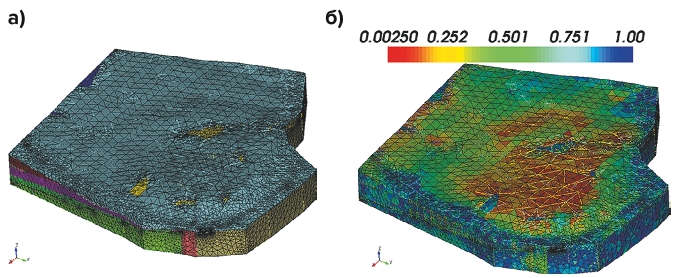 Рис. 4 Конечно-элементная сетка численной модели: а – общий вид; б – качество сетки по критерию формы
Рис. 4 Конечно-элементная сетка численной модели: а – общий вид; б – качество сетки по критерию формы
Fig. 4 Finite element mesh of the numerical model: а) general view, б) mesh quality in terms of its shape
Элементы с низким рангом качества расположены в слое четвертичных отложений, таким образом, они не виляют на расчетную зону (слой продуктивного ангидрита). Ввиду того что понижение ранга качества сетки в данном слое объясняется тем, что построенная сетка достаточно грубая, а сам слой имеет множество выклиниваний с толщиной менее 1 м, то при необходимости переноса расчетной зоны в данный слой необходимо выполнить сгущение сетки по выклиниваниям.
Четвертый этап подразумевал разработку логики пошагового расчета с учетом замены физико-механических свойств и отключения блоков.
Расчет физико-механических свойств массива выполнялся с учетом рейтинговых показателей по эмпирическим з ависимостям [17; 18]:
![]() (1)
(1)
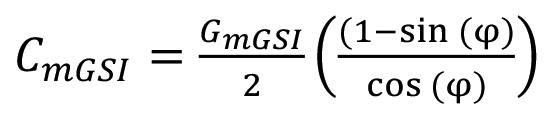 (2)
(2)
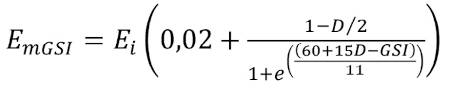 (3)
(3)
где σсж – предел прочности на одноосное сжатие образца, Па; Ei – модуль упругости образца, Па; GSI – geological strength index, определялся на основании индекса Q (по Бартону), полученному по результатам картирования; D – параметр нарушенности взрывными работами, принят равным 0; φ – угол внутреннего трения, град.
Физико-механические характеристики разупрочненного ангидрита являются пониженными характеристиками обычного. Понижение производилось ввиду общей нарушенности массива. Физико-механические характеристики материалов приведены в табл. 1.
Таблица 1 Физико-механические характеристики массива
Table 1 Physical and mechanical properties of the rock mass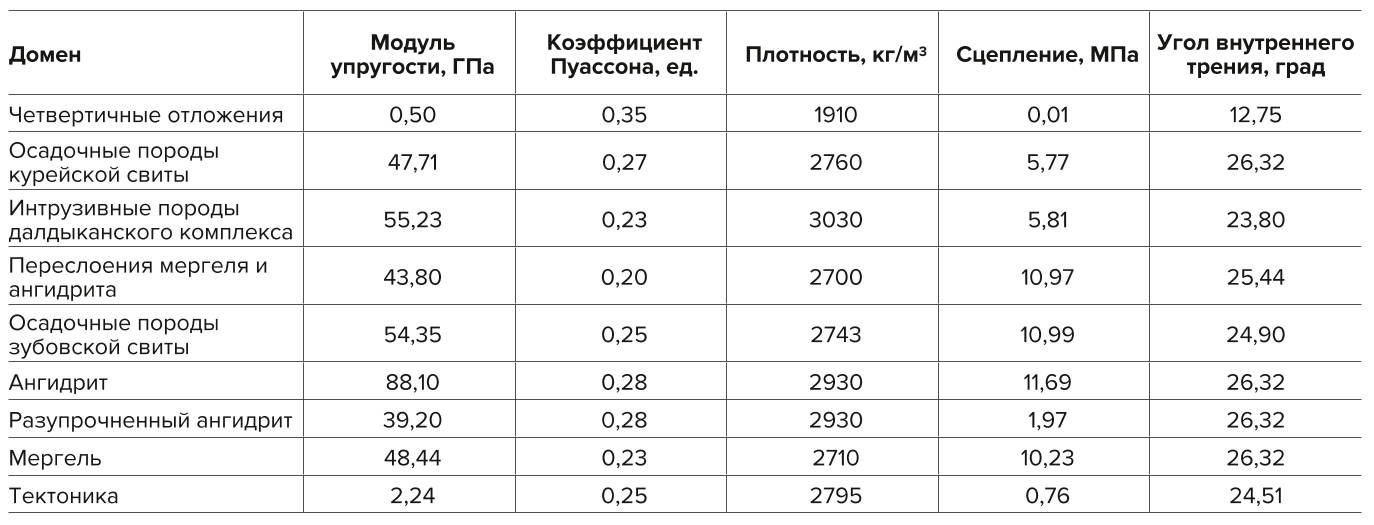
Моделирование выполняется в два шага:
1. Шаг 1: моделируется природное напряженно-деформированное состояние массива («greenfield»), в котором учитывается только собственный вес массива горных пород;
2. Шаг 2: моделируется отработка выработок и образование целиков в массиве.
На пятом этапе выполнялись расчет конечно-элементной модели в упруго-пластичной постановке с критерием Друкера-Прагера, а также анализ полученных результатов и их верификация путем сравнения с данными натурных наблюдений.
Рассмотрим максимальные главные напряжения по слою продуктивного ангидрита. Напряжения приведены на рис. 5. Зоны с наибольшими напряжениями по почве и кровле выделены красным контуром.
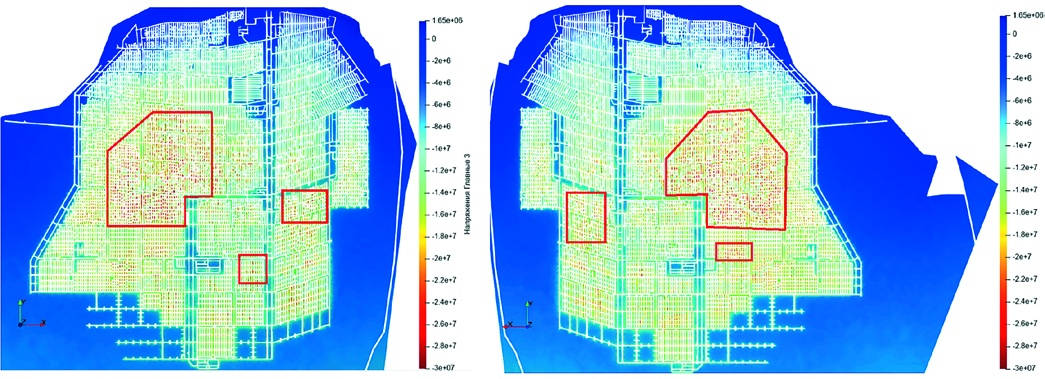 Рис. 5 Максимальные главные напряжения, Па, по слою продуктивного ангидрита: а – по кровле; б – по почве
Рис. 5 Максимальные главные напряжения, Па, по слою продуктивного ангидрита: а – по кровле; б – по почве
Fig. 5 Maximum principal stresses for the commercial anhydrite layer: а) for the superface, Pa, б) for the floor, Pa
Полученные при численном моделировании зоны довольно точно отображают осложнения в рамках эксплуатации шахты «Ангидрит». Таким образом, можно сделать вывод о качественном совпадении распределения напряжений в скальном массиве.
Рассмотрим максимальные главные напряжения по почве слоя мергелей, который находится непосредственно над слоем продуктивного ангидрита (рис. 6).
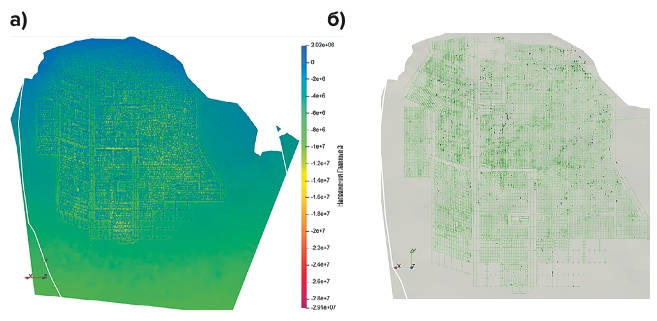 Рис. 6 Максимальные главные напряжения, Па, по почве слоя мергелей: а – общий вид; б – зоны растягивающих напряжений (черный цвет) с наложенными контурами выработок
Рис. 6 Максимальные главные напряжения, Па, по почве слоя мергелей: а – общий вид; б – зоны растягивающих напряжений (черный цвет) с наложенными контурами выработок
Fig. 6 Maximum principal stresses, Pa, for the floor of the marl layer: а) a general view; б) zones of tensile stresses (black colour) with superimposed excavation boundaries
Как видно на рисунке выше, по почве слоя мергелей присутствуют растягивающие напряжения с величиной до 2 МПа. Исходя из рисунка 6, б следует, что их распространение ограничено кровлей выработок, что соответствует действительности. При ведении очистных работ обязательным является крепление кровли выработок анкерами во избежание вывалов породы.
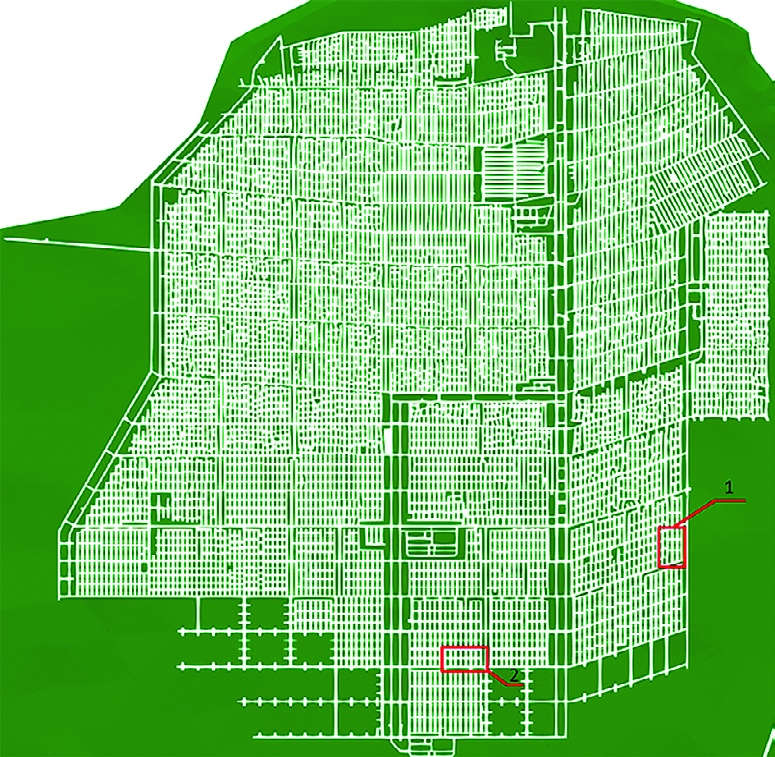 Рис. 7 Анализируемые участки
Рис. 7 Анализируемые участки
Fig. 7 Analyzed sections
Первый анализируемый участок приведен на рис. 8. По результатам численного моделирования видно, что зоны пластических деформаций на левой стороне целика больше, чем на правой. Также видно увеличение зоны пластических деформаций в центральной части целика. Если рассмотреть реальный целик, представленный на рис. 8, б, то видно, что он имеет форму «песочных часов», чтоуказывает на развитие больших зон разрушения в его центральной части (что качественно сопоставимо с картиной численного моделирования).
 Рис. 8 Анализируемый участок №1: а – результаты численного моделирования; б – состояние отмеченного целика
Рис. 8 Анализируемый участок №1: а – результаты численного моделирования; б – состояние отмеченного целика
Fig. 8 Analyzed section No.1: а) numerical simulation results, б) condition of the marked pillar
Аналогично видно, что левая часть целика имеет более значительные повреждения, чем правая, что также заметно по результатам численного моделирования. Однако, стоит отметить, что ввиду того что физико-механические характеристики понижались для всего целика, а не только для разупрочненных зон, участки пластических деформаций в массиве, полученные по результатам численного моделирования, существенно выше, чем в реальности. Кроме того, не удалось добиться количественной сходимости результатов, что указывает на необходимость решения локальных задач для оценки местных особенностей поведения массива.
 Рис. 9 Анализируемый участок №2: а – результаты численного моделирования; б – состояние отображенных целиков
Рис. 9 Анализируемый участок №2: а – результаты численного моделирования; б – состояние отображенных целиков
Fig. 9 Analyzed section No.2: а) numerical simulation results, б) condition of the indicated pillars
Второй анализируемый участок приведен на рис. 9. По результатам численного моделирования видно, что величина пластических деформаций больше в центральной части целиков. Также видно, что в целиках, расположенных с левой стороны, пластические деформации уменьшаются от ближних к дальним. Схожая качественная картина наблюдается и в реальности: целики приобретают форму песочных часов, однако разрушенная зона уменьшается от ближних целиков к дальним. Стоит отметить, что как в численном модели, так и в реальности, наблюдается еще одна особенность: целики на данном участке сильнее разрушены в верхней их части (по результатам численного моделирования, величина пластических деформаций в верхней части целиков выше, чем в нижней). Несмотря на качественную схожесть результатов, при анализе данного участка присутствуют такие же проблемы, как при анализе предыдущего.
Выполнение локального моделирования на базе глобальной численной модели
Примером выполнения локального моделирования на базе глобальной численной модели шахты «Ангидрит» является расчет устойчивости целиков при их повреждении в процессе нарезных и очистных работ от ведения буровзрывных работ. Целью данного расчета было определение максимального отклонения ширины междукамерного целика от проектных размеров.
Зона моделирования была выбрана на основе глобальной численной модели как одна из наиболее опасных по величине главных максимальных напряжений. Основная часть геометрии для выполнения локального расчета была взята из глобальной численной модели ввиду ее высокой детализации. Дополнительно была проработана основная расчетная зона: уточнено расположение вентиляционно-транспортных сбоек, учтен шаг уменьшения ширины целиков (на каждом этапе ширина междукамерного целика уменьшалась на 0,1 м). Общий вид модели приведен на рис. 10.
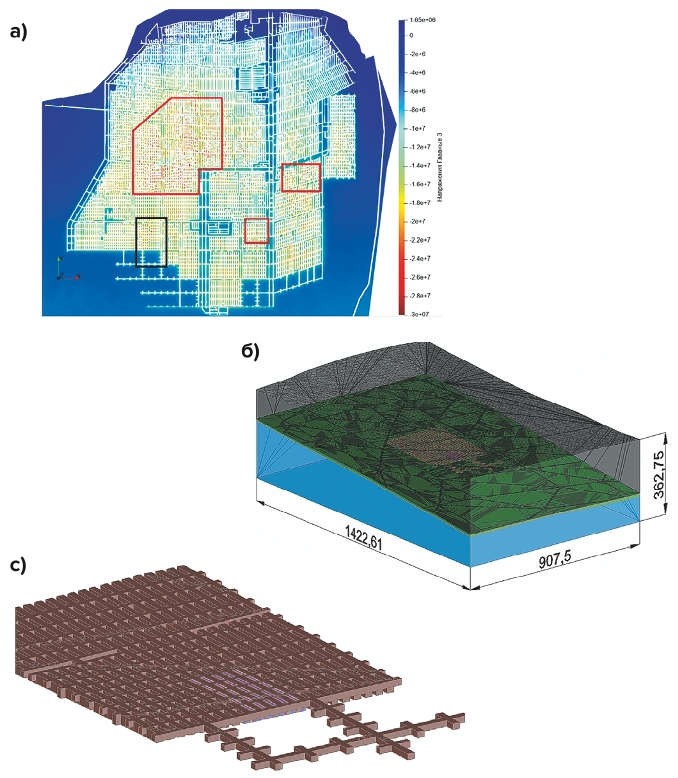 Рис. 10 Локальная численная модель: а – расположение участка локальной модели на глобальной (выделено черным); б – общий вид; в – детально смоделированный участок шахты
Рис. 10 Локальная численная модель: а – расположение участка локальной модели на глобальной (выделено черным); б – общий вид; в – детально смоделированный участок шахты
Fig. 10 A local numerical model: а) location of the local model section within the global model (highlighted in black), б) a general view, c) a mine section modelled in detail
Как видно из рис. 10, модель состоит из четырех основных частей: детально смоделированного участка шахты «Ангидрит», слоя продуктивного ангидрита, двух слоев скального массива (выше и ниже слоя продуктивного ангидрита). Ввиду того что основное влияние на поведение целиков будет оказано горным давлением от веса вышележащих скальных пород, для упрощения численной модели они были смоделированы единым слоем с присвоением медианных физико-механических характеристик. Размеры модели выбирались исходя из условия наличия дополнительного скального массива, который обеспечивает выполнение условия отсутствия краевых эффектов в расчетной зоне.
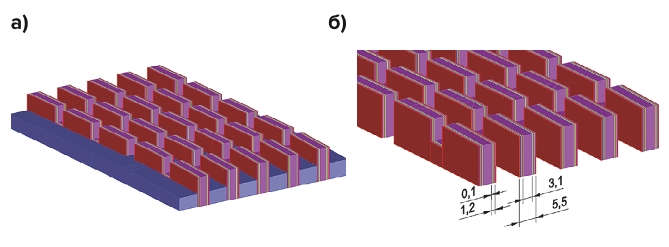 Рис. 11 Интересующий расчетный участок: а – общий вид; б – размеры элементов геометрии для моделирования изменения ширины целиков
Рис. 11 Интересующий расчетный участок: а – общий вид; б – размеры элементов геометрии для моделирования изменения ширины целиков
Fig. 11 The design section of interest: а) a general view, б) dimensions of geometry elements for modelling the changes in the pillar widths
Общий вид расчетной зоны приведен на рис. 11.
Из рис. 11 видно, что для моделирования устойчивости целиков была достаточно сильно уточнена часть геометрии численной модели. Целики были перерисованы в соответствии с проектом, также было уточнено расположение вентиляционно-транспортных сбоек. Максимально допустимая величина уменьшения поперечного размера целика была принята 1,2 м с каждой стороны (2,4 м в сумме), а шаг изменения ширины – 0,1 м.
Расчет выполнялся в CAE Fidesys. Общий вид схемы с построенной сеткой конечных элементов приведен на рис. 12. Сетка конечных элементов состоит из 4 356 551 тетраэдров и 1 177 696 узлов.
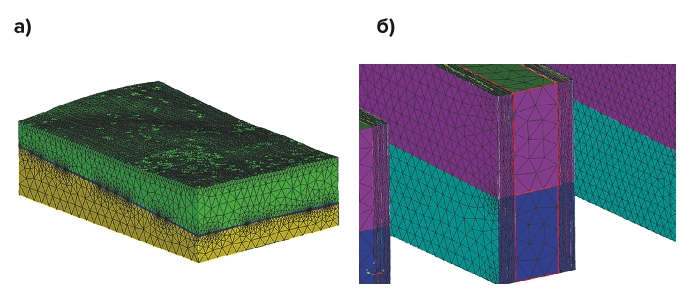 Рис. 12 Расчетная схема с построенной сеткой конечных элементов: а – общий вид; б – уточнение сетки конечных элементов на целиках
Рис. 12 Расчетная схема с построенной сеткой конечных элементов: а – общий вид; б – уточнение сетки конечных элементов на целиках
Fig. 12 Calculation model with the developed finite element mesh: а) general view, б) refinement of the finite element mesh on the pillars
Расчет выполнялся в 15 этапов:
1. Шаг 1: восстановление природного напряженно-деформированного состояния;
2. Шаг 2: формирование выработок;
3. Шаг 3: моделирование очистных работ в расчетной зоне;
4. Шаги 4–15: поэтапное уменьшение ширины целика с шагом 0,1 м.
Анализ результатов выполнялся пошагово. Рассматривалось развитие зон с запасом прочности меньше 1. Анализ результатов для некоторых шагов приведен на рис. 13. Согласно изоповерхностям распределения запаса прочности (рис. 13) видно, что целики разрушаются на полное сечение (т.е. запас прочности по Кулону-Мору <1 на шаге 10 (–140 см).
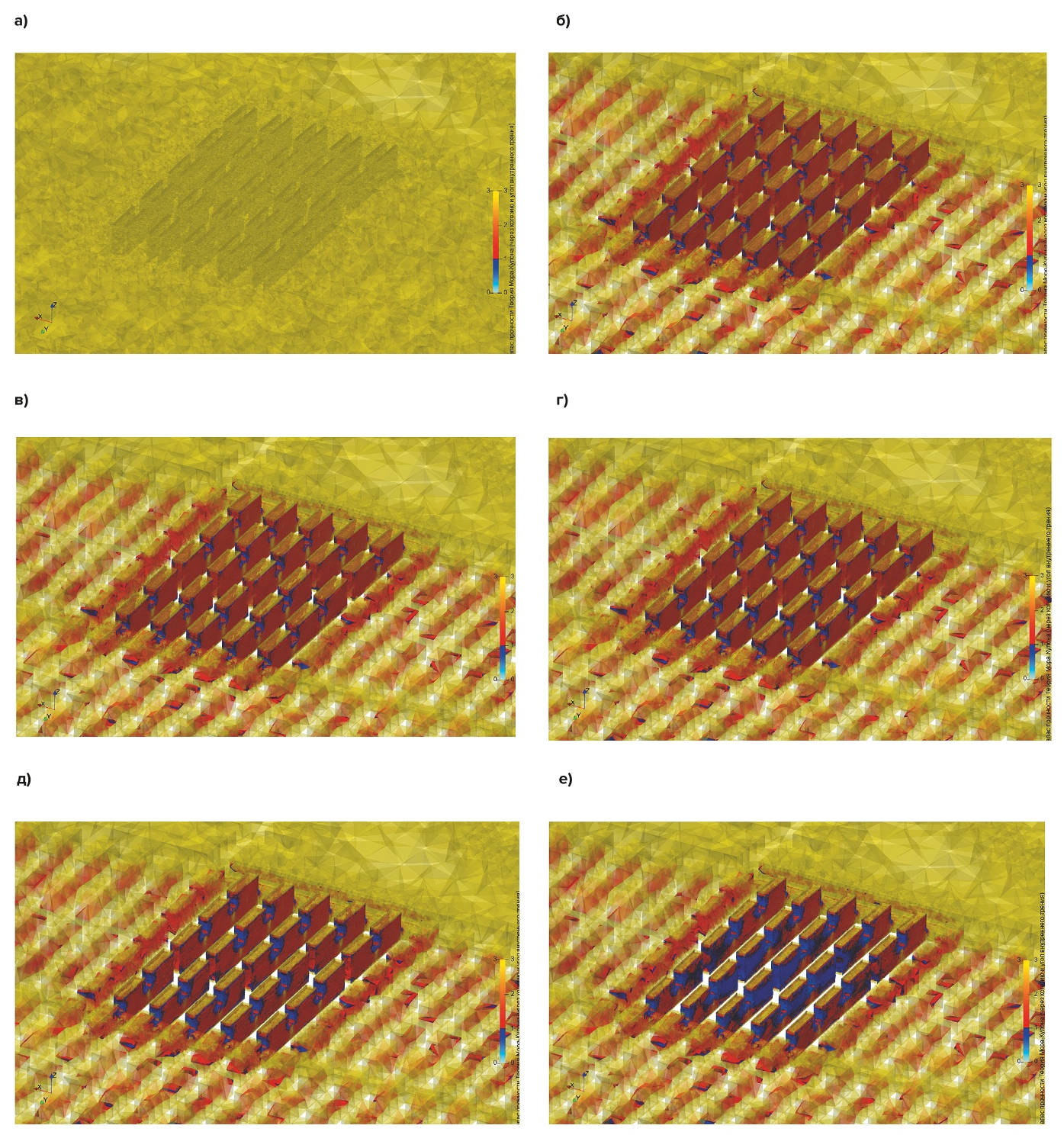 Рис. 13 Развитие зон с запасом прочности меньше 1 (синие зоны): а – шаг 1 – зоны отсутствуют; б – шаг 3 – присутствуют незначительные зоны с низким запасом прочности в местах концентрации напряжений; в – шаг 5 – суммарное уменьшение ширины целика на 40 см, наблюдается незначительный рост зон с запасом прочности меньше 1 в торцах целика; г – шаг 6 – суммарное уменьшение ширины целика на 60 см, зоны незначительно развиваются; д – шаг 10 – суммарное уменьшение ширины целика на 140 см, зоны с запасом прочности меньше 1 существенно увеличились, начинается распространение зон на боковую поверхность целиков; е – шаг 13 – суммарное уменьшение ширины целика на 200 см, большая часть целиков имеет запас прочности меньше 1
Рис. 13 Развитие зон с запасом прочности меньше 1 (синие зоны): а – шаг 1 – зоны отсутствуют; б – шаг 3 – присутствуют незначительные зоны с низким запасом прочности в местах концентрации напряжений; в – шаг 5 – суммарное уменьшение ширины целика на 40 см, наблюдается незначительный рост зон с запасом прочности меньше 1 в торцах целика; г – шаг 6 – суммарное уменьшение ширины целика на 60 см, зоны незначительно развиваются; д – шаг 10 – суммарное уменьшение ширины целика на 140 см, зоны с запасом прочности меньше 1 существенно увеличились, начинается распространение зон на боковую поверхность целиков; е – шаг 13 – суммарное уменьшение ширины целика на 200 см, большая часть целиков имеет запас прочности меньше 1
Fig. 13 Extension of zones with the safety margin less than 1 (blue zones): а) step 1 – no zones; б) step 3 – minor low safety margin zones are present in stress concentration areas; в) step 5 – cumulative reduction of the pillar width by 40 cm, there is an insignificant growth of zones with safety margin less than 1 at the pillar ends; г) step 6 – cumulative reduction of the pillar width by 60 cm, zones are slightly developing; д) step 10 – total reduction of the pillar width by 140 cm, zones with the safety margin less than 1 have significantly increased, zones are beginning to expand to the lateral surface of the pillars; е) step 13 – total reduction of the pillar width by 200 cm, most of the pillars have the safety margin less than 1
Таким образом, можно сделать вывод, что при заданных горно-геологических условиях прочности пород, при отсутствии перебора породы вследствие взрывных работ при нарезке и соблюдении параметров ведения горных работ в исключительных случаях возможно проведение очистных работ при уменьшении ширины целика от проектной величины на 80–100 см, значение 140 см является предельным и в отдельных случаях, при неблагоприятном расположении трещин и пр., может приводить к разрушению целика. Последнее может стать причиной перераспределения напряжений на близлежащие целики, тем самым перегрузив их и запустив цепную реакцию обрушения.
На рис. 14 приведен один из целиков, находящийся в рамках расчетной зоны. По результатам натурных измерений суммарное уменьшение ширины целика составило 80 см, что подтверждает результаты численного моделирования. Как видно, по аналогии с результатами, наблюдается разрушение углов в торце, однако целик остается устойчивым.
 Рис. 14 Целик, находящийся в рамках расчетной зоны
Рис. 14 Целик, находящийся в рамках расчетной зоны
Fig. 14 A pillar located within the calculation zone
Стоит учитывать, что математическая модель является наиболее приближенной к реальности по сравнению с аналитическими методами, однако она не дает стопроцентной точности расчета, т.к. невозможно учесть все факторы, которые возникают в конкретной выработке или целике. Также не допускается более двух целиков подряд с уменьшенной шириной, т.к. это будет способствовать перераспределению давления на соседние целики, что может служить причиной их разрушения.
Заключение
В статье представлена методология формирования глобальных детализированных численных моделей в CAE Fidesys с использованием САПР AutoCAD и дополнительного программного обеспечения для обработки геометрии, разработанного на языке программирования Python. Совместное использование данных инструментов позволило создать глобальную численную модель шахты «Ангидрит» с высокой детализацией литологии расчетного участка, а также камерно-столбовой системы отработки, используемой в шахте.
По результатам численного моделирования были получены зоны повышенного давления в рамках шахты «Ангидрит». Данные зоны совпадают с наиболее опасными участками в реальности. Таким образом, было верифицировано качественное распределение напряжений на расчетном участке.
По результатам выполнения расчета были получены зоны растягивающих напряжений в почве слоя мергелей, что соответствует реальности. Развитие подобных участков может провоцировать вывалы породы, исходя из чего происходит крепление кровли всех выработок.
Исходя из анализа пластических деформаций целиков и их сравнения с аналогичными реальными целиками можно сделать вывод о качественной схожести результатов численного моделирования и реального поведения скального массива. Это позволяет производить не только укрупненную оценку НДС расчетных участков, но и определять наличие локальных особенностей.
Несмотря на то что поведение численной модели схоже с поведением массива на шахте «Ангидрит», следует учитывать, что глобальная численная модель в первую очередь предназначена для получения укрупненных результатов и моделирования глобальных изменений в эксплуатации подземного сооружения. Несмотря на то что рассмотренная модель позволяет отследить качественные проявления локальных особенностей поведения массива, она не дает возможности количественно оценить величину зон разрушения, а также локальное напряженно-деформированное состояние. Анализ подобных моделей должен выполняться в первую очередь с целью определения наиболее опасных зон, которые в дальнейшем необходимо отдельно рассчитывать в виде локальных численных моделей.
Методология построения численных моделей от глобальных к локальным, является наиболее корректной при решении производственных задач. Она позволяет укрупненно определить наиболее опасные участки, а также увидеть возможные местные особенности поведения массива в глобальной модели, а в локальной – детально смоделировать данный участок, получив результаты, количественно и качественно приближенные к реальности. Таким образом, подобный подход обеспечивает наиболее продуктивный и оперативный вариант численного анализа крупных подземных сооружений.
Одновременное использование глобальной и локальной численных моделей в данной статье позволило не только решить производственную задачу в сжатые сроки, но и получить достаточно высокую сходимость с натурными наблюдениями. Благодаря численному моделированию было определено, что возможно проведение очистных работ при уменьшении ширины целика от проектной величины на 80–100 см, значение 140 см является предельным и в отдельных случаях, при неблагоприятном расположении трещин и пр., может приводить к разрушению целика.
Применение детальных глобальных численных моделей на текущий момент затруднено ввиду значительных трудоемкости и наукоемкости их создания. Главной проблемой является оптимизация исходной твердотельной геометрии для нужд численного моделирования. При исходной геометрии низкого качества полученные результаты могут быть сложно анализируемыми ввиду большого количества концентраторов напряжений. Помимо этого, теряется основная суть детальных глобальных моделей: возможность укрупненного представления о локальных процессах. Кроме того, иногда низкое качество геометрии делает невозможным построение подобной модели в целом. Использование разработанного дополнительного программного обеспечения для оптимизации геометрии позволяет решить данную проблему, что обеспечивает возможность формирования глобальных численных моделей.
Список литературы
1. Зубов В.П., Анисимов К.А. Ресурсосберегающая технология подземной отработки запасов алмазосодержащих кимберлитовых рудных тел ниже дна карьера под защитной подушкой. Горный журнал. 2023;(4):23–38. https://doi.org/10.17580/gzh.2023.04.05
2. Чебан А.Ю. Технология комбайновой выемки тонких рудных жил смешанным забоем. Горный информационно-аналитический бюллетень. 2021;(6):145–152. https://doi.org/10.25018/0236_1493_2021_6_0_145
3. Петров А. Н., Петрова Л. В., Сивцева А. И., Алексеев А. М. Отработка нижних горизонтов золоторудного месторождения «Бадран» с применением самоходного оборудования. Известия Тульского государственного университета. Науки о Земле. 2019;(2):175–184.
4. Соннов М.А., Румянцев А.Е., Трофимов А.В., Вильчинский В.Б. Геотехническое обоснование отработки залежей, ограниченных тектоническими нарушениями на основе применения конечно-элементного моделирования. Горная промышленность. 2018;(5):107–110. https://doi.org/10.30686/1609-9192-2018-5-141-107-110
5. Хохлов С.В., Виноградов Ю.И., Носков А.П., Баженова А.В. Прогнозирование смещения рудных контуров при формировании развала взорванной горной массы. Горный информационно-аналитический бюллетень. 2023;(3):40–56. https://doi.org/10.25018/0236_1493_2023_3_0_40
6. Wang Y., Huang J., Wang G. Numerical analysis for mining-induced stress and plastic evolution involving influencing factors: High in situ stress, excavation rate and multilayered heterogeneity. Engineering Computations. 2022;39(8):2928–2957. https://doi.org/10.1108/EC-10-2021-0614
7. Jing L., Hudson J.A. Numerical methods in rock mechanics. International Journal of Rock Mechanics and Mining Sciences. 2002; 39(4):409–427. https://doi.org/10.1016/S1365-1609(02)00065-5
8. Bobet A. Numerical methods in geomechanics. Arabian Journal for Science and Engineering. 2010;35(1B):27–48.
9. Li J., Shen C., He X., Zheng X., Yuan J. Numerical solution for circular tunnel excavated in strain-softening rock masses considering damaged zone. Scientific Reports. 2022;12:4465. https://doi.org/10.1038/s41598-022-08531-3
10. Xi P., Huo Y., Zhu D., Xing C., Wang Z. Development and application of triangulation joint network based on an FEM program (RS2). Journal of Geophysics and Engineering. 2022;19(2):245–254. https://doi.org/10.1093/jge/gxac013
11. Господариков А.П., Киркин А.П., Трофимов А.В., Ковалевский В.Н. Определение физико-механических свойств горных пород при применении противоударных разгрузочных мероприятий. Горный журнал. 2023;(1):26–34. https://doi.org/10.17580/gzh.2023.01.04
12. Бирючев И.В., Макаров А.Б., Усов А.А. Геомеханическая модель рудника. Часть 1. Создание. Горный журнал. 2020;(1):42–48. https://doi.org/10.17580/gzh.2020.01.08
13. Рассказов М.И., Цой Д.И., Крюков В.Г., Потапчук М.И., Федотова Ю.В. Изучение горно-геологических особенностей и определение физико-механических свойств горных пород золоторудного Албынского месторождения. Горный информационно аналитический бюллетень. 2021;(5-2):146–161. https://doi.org/10.25018/0236_1493_2021_52_0_146
14. Марысюк В.П., Сабянин Г.В., Трофимов А.В., Колганов А.В. Методология построения блочной геомеханической модели горного массива в поле рудника «Таймырский». Горный журнал. 2022;(10):39–45. https://doi.org/10.17580/gzh.2022.10.06
15. Писецкий В.Б., Лапин С.Э., Левин В.А., Горбунов В.А., Чевдарь С.М. О выборе критерия оценки риска потери состояния устойчивости горного массива по сейсмическим, аэрогазовым и геомеханическим данным. В кн.: Безопасность труда и эффективность производства горнодобывающих предприятий с подземным способом разработки: материалы 1-й междунар. науч.-техн. конф., г. Екатеринбург, 6 апреля – 7 июня 2016 г. Екатеринбург: Уральский государственный горный университет; 2016. С. 59–65.
16. Dang V.K., Do N.A., Dinh V.D. Estimating the radial displacement on the tunnel boundary by rock mass classification systems. International Journal of GEOMATE. 2022;22(92):9–15. https://doi.org/10.21660/2022.92.19
17. Hoek E., Diederichs M.S. Empirical estimation of rock mass modulus. International Journal of Rock Mechanics and Mining Sciences. 2006;43(2):203–215. https://doi.org/10.1016/j.ijrmms.2005.06.005
18. 18. Vasarhelyi B., Kovacs D. Empirical methods of calculating the mechanical parameters of the rock mass. Periodica Polytechnica Civil Engineering. 2017;61(1):39–50. https://doi.org/10.3311/PPci.10095








