Постановка многокритериальной задачи анализа и прогнозирования гранулометрического состава взорванных горных пород

А.В. Дремин¹, В.С. Великанов^{1, 2, 3
1} ООО «ДАВТЕХ», г. Екатеринбург, Российская Федерация
² Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, г. Екатеринбург, Российская Федерация
³ Уральский государственный горный университет, г. Екатеринбург, Российская Федерация
Горная Промышленность №5 / 2023 стр. 52-60

Резюме: Изменение горно-геологических характеристик месторождений твердых полезных ископаемых, резкое снижение содержания полезного компонента в руде на многих месторождениях твердых полезных ископаемых и интенсификация открытой геотехнологии обусловливают необходимость разработки научно-теоретических и методологических основ, определяющих повышение эффективности процесса взаимодействия технологических элементов в рамках концепции «карьер–фабрика» («mine-to-mill», М2М), которые могут быть адаптированы под каждое конкретное горнодобывающее предприятие и позволят оптимизировать производственные затраты. Буровзрывные работы – основная технологическая операция отделения горной породы от массива и дробления горной массы при добыче твердых полезных ископаемых. Основная цель проведения буровзрывных работ состоит в формировании горной массы, обладающей необходимыми характеристиками для бесперебойного и эффективного взаимодействия с горной техникой на последующих этапах разработки месторождения с учетом технико-экономических затрат. Формирование развала отбитой горной породы взрывом влияет на последующие технологические переделы горного производства, а следовательно, на себестоимость конечной продукции горного предприятия. Целью исследования явилась разработка математической модели прогнозирования и анализа гранулометрического состава взорванных пород в системе взаимодействия элементов «карьер–фабрика». Используемые методы: комплексный подход, который включает: научный анализ и обобщение ранее опубликованных исследований. Методологическую основу исследований составляют методы системного анализа, а также использование информационных технологий.

Ключевые слова: добыча, полезное ископаемое, буровзрывной способ, карьер, гранулометрический состав, математическая модель

Для цитирования: Дремин А.В., Великанов В.С. Постановка многокритериальной задачи анализа и прогнозирования гранулометрического состава взорванных горных пород. Горная промышленность. 2023;(5):52–60. https://doi.org/10.30686/1609-9192-2023-5-52-60

Информация о статье

Поступила в редакцию: 25.09.2023

Поступила после рецензирования: 09.10.2023

Принята к публикации: 09.10.2023

Информация об авторах

Дремин Александр Владимирович – генеральный директор, ООО «ДАВТЕХ», г. Екатеринбург, Российская Федерация

Великанов Владимир Семенович – доктор технических наук, научный консультант, ООО «ДАВТЕХ», профессор кафедры подъемно-транспортных машин и роботов, Уральский федеральный университет имени первого президента России Б.Н. Ельцина, г. Екатеринбург, Российская Федерация, профессор кафедры автоматики и компьютерных технологий, Уральский государственный горный университет, г. Екатеринбург, Российская Федерация; https://orcid.org/0000-0001-5581-2733; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

Основная задача горного производства – оптимизировать всю технологическую цепочку этапов добычи и переработки полезных ископаемых, при этом в рамках решения задачи необходимо рассматривать каждый технологический процесс как отдельно, так и в комплексе [1].

Буровзрывные работы (БВР) – это начальный этап добычи и широко используются при извлечении твердых полезных ископаемых, причем 15–30% энергии взрывчатых веществ (ВВ) идет на процесс дробления горных пород. Технология ведения буровзрывных работ постоянно совершенствуется. Внедрение на горнодобывающих предприятиях инновационных технологических решений, цифровых технологий для отдельных геологических, маркшейдерских и технологических задач направлено на минимизацию затрат на всех этапах добычи и переработки [1]. Вместе с тем актуальной проблемой в области буровзрывных работ, определяющей себестоимость и безопасность горных работ, остаются развал горной массы и его параметры (в основном гранулометрический состав – процентное содержание величины кусков одинакового размера (фракции) относительно общего объема взорванной массы. В англоязычных научных публикациях используется термин «фрагментация»). Доказано, что снижение эксплуатационной производительности и повышение себестоимости горных работ из-за нерациональных параметров развала весьма значительны. Так, например, при увеличении мелкой доли фракции с размером до 0,2 м в два раза производительность экскаватора-драглайна увеличивается в три раза, также в три раза производительность снижается при увеличении доли фракции 0,4–0,6 м в 5 раз, и фракции 0,21–0,4 м в 1,4 раза, а временные затраты, необходимые для подготовки и производства взрыва, в 5–8 раз меньше времени простоев, возникающих при некачественном взрыве [1–3].

Отметим также, что планирование и выполнение БВР с опорой на качественные и количественные показатели итогового распределения грансостава развала позволяют сократить общие затраты и устранить характерные для БВР неблагоприятные воздействия на окружающую среду: взрывное разрушение вглубь массива, вибрацию, образование пыли, разлет кусков породы и шум.

В работе [1] установлено, что предпринимавшиеся попытки теоретического обоснования физического процесса формирования гранулометрического состава (грансостава) в развале горной массы в увязке со сложной проблемой дробления горных пород взрывом не нашли реализации в разработке пригодных для практики расчетных методик прогнозирования грансостава развала.

Невозможность игнорирования существующей проблематики привела к тому, что в рамках научно-исследовательских работ (НИР) по изучению грансостава взорванных скальных пород, осуществляемых компанией «ДАВТЕХ», решается задача разработки математического и программного обеспечения, позволяющего оперативно обрабатывать большие объемы данных, а именно изображений развала горной массы, полученных в ходе исследований на конкретных месторождениях горнодобывающих предприятий, и получения точной прогнозной информации по грансоставу, необходимой для использования в цепочке взаимодействия технологических машин (конвейеры, грохоты, дробилки и другое оборудование) системы «карьер–фабрика».

Материалы и методы

Библиометрический анализ основных направлений развития НИР по установлению методов оценки распределения грансостава показал значительный рост числа публикаций за последнее десятилетие, в лидерах по количеству опубликованных работ являются КНР, США и ряд западноевропейских стран. В работе [4] представлен развернутый и детальный анализ научно-исследовательских работ по методам оценки распределения грансостава взорванных горных пород. Установлено, что используются неконтролируемые методы, основанные на физико-механических свойствах горных пород, и контролируемые методы, зависящие от проектных факторов, таких как оценка распределения по размерам и прогнозирование раздробленных горных пород. В свою очередь, контролируемые методы делятся на прямые и косвенные. Прямым методом, который является более надежным для определения распределения раздробленных пород, является ситовый анализ, он достаточно точный. Понятно, что в условиях действующих горнодобывающих предприятий с поточной технологией переработки добытого сырья сложность заключается главным образом в том, что для получения объективной информации по фракционному распределению раздробленных пород требуются значительные временные и материальные затраты. Косвенные же методы, включая эмпирические и методы обработки и анализа изображений, обеспечивают желаемый компромисс между точностью и количеством затраченного времени. Отдельные разработки посвящены методам измерения грансостава взорванной горной массы, использующим оптическую визуализацию или лазерное сканирование и собственное программное обеспечение (ПО, Soft) для определения гранулометрического состава.

Методы обработки и анализа изображений нашли широкое применение в промышленном производстве, искусстве, медицине, космосе, при управлении процессами автоматизации обнаружения и распознавании образов (изображения, создаваемые электронными микроскопами, рентгеновскими аппаратами, томографами и т. д.) [5; 6].

Востребованность и актуальность данных исследований несомненна, в зарубежной и отечественной литературе приводится большой класс алгоритмов обработки цифровых изображений, которые могут применяться для решения значительного спектра задач, описаны основные направления обработки и анализа изображений, включая основы теории восприятия и регистрации видеоинформации, методы фильтрации, вейвлет-преобразования, улучшения, восстановления и сжатия черно-белых и цветных изображений. Обсуждаются также вопросы сегментации, распознавания образов, описания и представления деталей, морфологического анализа изображения. В основном приведенные в работах модели и алгоритмы реализованы в системе MatLab. Вместе с тем существующее предложение по программам обработки изображений, которые были разработаны и позволяют быстро и точно оценивать распределение грансостава [7–14], представлено зарубежными IT-компаниями и их ПО. Данный подход ориентирован на использование мощных компьютеров, имеющих в своем составе пакеты обработки изображений, например, IPACS, Tucips, FragScan, CIAS, GoldSize, WipFrag, Split, Power Sieve и Fragalyst. Системы Split-Desktop (рис. 1), WipFrag (впервые предложена в 1987 г. и коммерциализирована в 1996 г.). FragScan и GoldSize являются наиболее популярными программными пакетами, основанными на обработке 2D-изображений для выполнения анализа распределения по размерам пород взрывного блока. Косвенный метод определения гранулометрического состава при фрагментации с помощью системы Split-Desktop предусматривает пять этапов: масштабирование изображения, выделение фрагментов породы для сегментации, выдачу разрешения на редактирование фрагментов породы, анализ отмеченных фрагментов и завершающий этап с отображением диаграммы гранулометрического состава.

 Рис. 1 Мобильное устройство компании Motion Metrics International Corp и изображения, полученные для анализа и их обрисовки с помощью программы Split-Desktop [15]

Fig. 1 A portable device by the Motion Metrics International Corp. and images obtained for analysis and outlining using the Split-Desktop software suite [15]

В работе [1] были определены два основных приоритетных направления исследований грансостава взорванных пород: прогнозирование гранулометрического состава исходя из условий и параметров БВР; оптимизация и автоматизация определения гранулометрического состава взорванных пород по их снимкам на разрабатываемых месторождениях.

В развитие приоритетных направлений нами решается комплекс задач по математическому обеспечению и внедрению «экспресс-метода», ориентированного на мобильное устройство с использованием процессоров, имеющих ограниченные ресурсы быстродействия, памяти и ограничения на встроенные методы обработки изображений, и не требующего, по возможности, участия человека при подготовке и обработке данных. В число производителей, активно развивающих данное направление с точки зрения технической реализации мобильных устройств, входят такие компании, как Metso, Motionmetrics (см. рис. 1), Innovative Machine Vision и Split Engineering. Компании Motion Metrics, Orica FRAGTrackTM и Split Engineering предлагают варианты размещения устройств измерения фрагментации горной массы на горнодобывающей технике, а именно на карьерных экскаваторах.

Систематизация параметров и показателей для создания математического описания гранулометрического состава взорванных пород. Объектом исследования является развал горной массы после проведения БВР, а основным предметом оценки – процентное соотношение кусков различных фракций. В соответствии с обозначенной целью исследований нами предлагается использование оригинального подхода, учитывающего взаимовлияние ряда факторов и позволяющего объединить в одной модели разнородные параметры и показатели для создания математического описания гранулометрического состава взорванных пород. Ключевые параметры и показатели, влияющие на формирование грансостава развала горной массы, условно можно разделить на две группы: природные (P₁) – исходные параметры взрываемого массива горных пород (свойства горной массы); технологические (P₂) – определяют способ и средства воздействия на массив (проектные параметры БВР) (табл. 1). К природным относятся характеристики массива горных пород (физико-механические свойства пород, направление трещиноватости, размер отдельности в массиве, тектонические нарушения, геометрия взрываемого блока и т. д.), в соответствии с приняты обозначением будут иметь индекс – P_1,i. Технологические параметры и показатели ориентированы и зависят от природных и могут быть представлены несколькими подгруппами: к первой относятся параметры размещения заряда в массиве (диаметр и высота заряда, сетка бурения, тип взрывчатого вещества (ВВ)), которые определяют удельный расход ВВ; ко второй можно отнести последовательность и направление инициирования скважинных зарядов ВВ, средства инициирования и др. – P_2,i.

 Таблица 1 Разнородные параметры и показатели для создания математического описания

Table 1 Various parameters and indicators for creating a mathematical description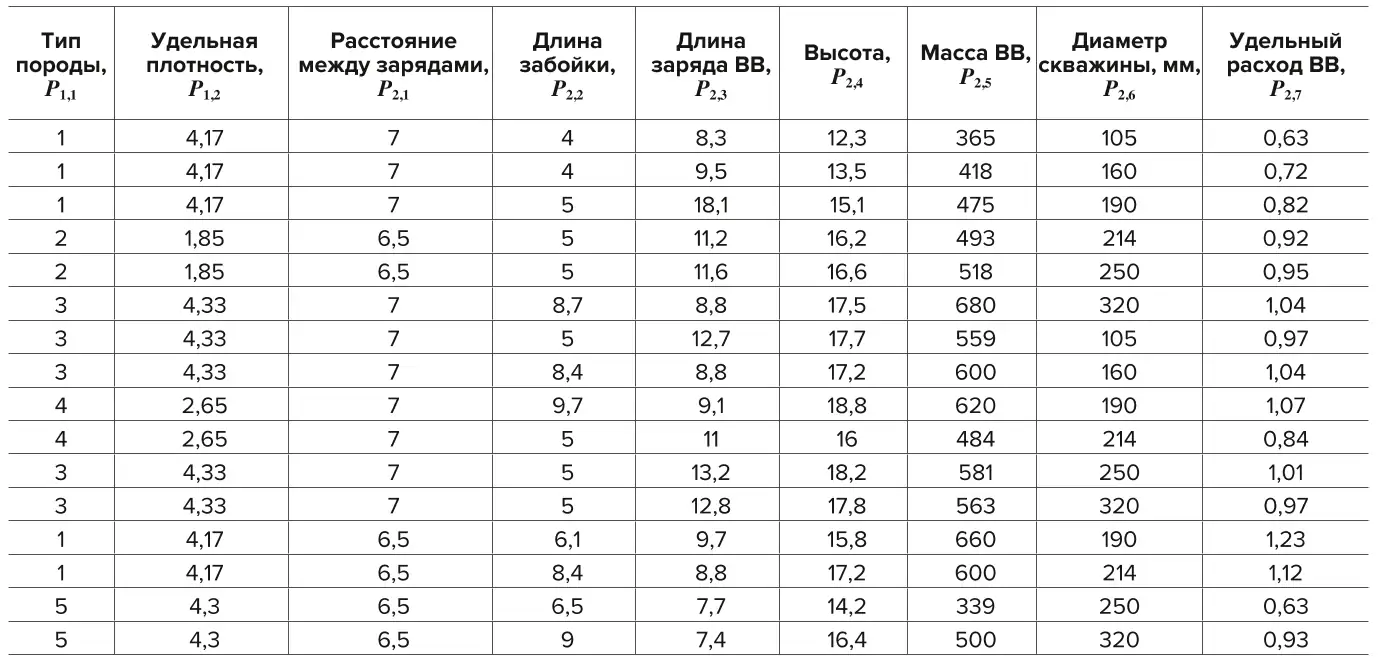

Указанные параметры и показатели (см. табл. 1) определяют основу построения модели с учетом их определяющего влияния (на основе весового коэффициента) в формировании грансостава развала горной массы. Весовой коэффициент – числовой коэффициент, параметр, отражающий значимость, относительную важность, «вес» параметра в сравнении с другими, оказывающими влияние на изучаемый процесс. В настоящее время существуют различные методы определения весовых коэффициентов, которые используют для решения различных задач в многокритериальных методах принятия решений (Multi-criteria decision making, MCDM). Субъективные методы определения веса основаны на экспертной оценке, т. е. определяются из суждений и в соответствии с предпочтениями ЛПР о данных критериях. Эффективность и качество оценки зависят от опыта, знаний и интуиции ЛПР и экспертов, численности экспертов (ЛПР) и степени согласия между ними. Наибольшее распространение в MCDM получили такие методы, как SMART, AHP, SIMOS и метод Delphi.

В методах объективного взвешивания вес определяется на основе информации, собранной по каждому критерию с использованием математических алгоритмов и моделей и без участия ЛПР. Наиболее распространенными методами являются метод наименьших средних квадратов (LMS), минимальное максимальное отклонение, энтропия, TOPSIS и многокритериальная оптимизация. Комбинированные подходы основаны на сочетании методов субъективного и объективного взвешивания на основе мультипликативного и аддитивного синтеза.

В работах [16–18] представлено оригинальное применение метода MCDM и определены основные достоинства и недостатки. А именно ключевые достоинства, отмеченные в данной работе: с использованием MCDM выполняется решение четырех типов проблем: выбор наилучшей альтернативы из множества, ранжирование и сортировка альтернатив, а также описание и систематизация решений и их последствий, для оценки и дальнейшего управления. Основная цель MCDM состоит в том, чтобы облегчить процесс принятия решения с учётом ценностей и целей всех стейкхолдеров в рамках решаемой проблемы. Это достигается в три ключевых этапа: выявление и структурирование проблемы; построение и использование моделей и разработка планов действий.

В ряде публикаций нами достаточно успешно использовались как субъективные методы – распределение баллов [19], методы ранжирования и парных сравнений [20; 21], так и объективные – среднеквадратичное отклонение и дисперсионный анализ [22], их применение было определено характером решаемых практических задач и областью научных исследований. Накопленный опыт (первые публикации датируются 2009 г.) и анализ различных методов в определении весовых коэффициентов позволили исходя из специфики решаемой проблемы предложить в качестве основного метода исследований – нечеткий аналитический иерархический процесс (Fuzzy AnalyticHierarchy Process, далее F-AHP). Основное принципиальное отличие F-AHP от классического метода анализа иерархий – это возможность снивелировать недостатки: несбалансированность шкалы суждений, неопределённость и субъективность суждения экспертов и одновременно повысить точность оценки.

Этапы F-AHP: построение начальной нечёткой матрицы попарного сравнения параметров (показателей); расчёт нечётких синтетических значений экстента для параметров (показателей); расчёт степени вероятности двух нечётких чисел M₁ и M₂; расчёт вектора приоритетов; расчёт нормализованных весовых векторов [17, 18]:

где Ã – нечеткая матрица попарного сравнения параметров (показателей); ũ_ij – нечеткое число, показывающее оценку степени влияния каждой пары параметров (показателей) между собой на пересечении i-й строки и j-го столбца

где S_i – нечеткие синтетические значения экстента для параметров (показателей); a, b, c – компоненты нечетких чисел треугольной функции принадлежности.

3. Степень вероятности того, что М2 = (a₂, b₂, c₂) > М1 = (a₁, b₁, c₁) определяется

где d – ордината самой высокой точки пересечения D между μ_М1(x) и μ_М2(y). Степень вероятности того, что выпуклое нечёткое число M больше, чем k выпуклых нечётких чисел M_i (i = 1, 2, 3, ..., k), определяется

где A_i (i = 1, 2, ..., n) – вектор оцениваемых параметров, состоящий из n элементов.

d'(A_i) = minV (S_i ≥ S_k), для k = 1, 2, ..., n; k≠i.

5. W = (d(A₁), d(A₂),..., d(A_n))T где W – нечеткое число.

Вообще говоря, известно свыше десятка типовых форм кривых для задания функций принадлежности нечетких множеств: треугольные, трапециевидные, гауссовы, двойные гауссовы, колоколообразные, сигмоидальные, двойные сигмоидальные, z-функции, s-функции и их обобщения. Наибольшее распространение получили кусочно-линейные (треугольные и трапециевидные) формы функций принадлежности.

Необходимо отметить, что на сегодняшний день в качественных моделях прогноза испытывают потребность многие отрасли, в том числе и горнодобывающая промышленность. Основная задача прогнозирования имеет целью по полученным ранее статистическим данным предсказать будущие значения изучаемого процесса, явления или системы, составить прогноз. При прогнозировании в основе лежит не только проведение аналитических исследований и подготовка базы данных, но и использование методов прогнозирования, способов и приемов расчетов будущих значений. В разрезе рассматриваемой тематики, исследуя существующие методы прогнозирования, можно дать ответы на следующие вопросы: какие методы возможно использовать при разработке прогнозов получения приемлемого грансостава при ведении БВР, насколько методическая база адекватна современным информационным технологиям и рыночным условиям функционирования горнодобывающих предприятий. В научно-технической литературе разработано и описано достаточно большое количество методов прогноза, но к основным можно отнести два: локальные и глобальные [23–25].

В настоящее время большинство горнодобывающих предприятий практически не используют научно обоснованные методы прогнозирования, к примеру, такие как статистические методы (различные экстраполяционные методы), экономико-математическое моделирование. Перспектива развития оценивается преимущественно на основе опыта и интуиции технического персонала и руководителей, а также методов аналогии. Главными причинами сложившейся ситуации послужили отсутствие на предприятиях современных методик прогнозирования, а также специалистов, владеющих методами прогнозирования и приемами по обработке исходной информационной базы (выделение трендовой, сезонной, циклической, случайной составляющих временных рядов) и приведению ее в сопоставимый вид.

Для прогнозирования и изучения сложных слабоформализуемых систем в условиях неопределенности используется подход на основе временных рядов, полученных в результате мониторинга, и нацеленный на извлечение знаний, полезных для прогнозирования. Bpeмeннoй ряд (ВР) – это последовательность дискретных упорядоченных в неслучайные равноотстоящие моменты времени измерений (показателей, наблюдений) y(t₁), y(t₂), …, y(t_n), характеризующих уровни состояний изучаемого процесса, протекающего в условиях неопределённости. Значения таких временных рядов изначально неточны и характеризуются внутренней неопределенностью. Основной идеей при моделировании таких временных рядов является использование моделей, позволяющих описывать неточности и неопределенности как в данных, так и в их динамике. Эта концепция основывается на понятии дискретных динамических процессов, для которых предполагается зависимость текущих состояний от предыдущих. Исторически наибольшее признание получили стохастические модели динамических процессов, в то же время, ввиду ограничений на длину ВР, в последнее время развиваются и успешно применяются альтернативные модели: нейросетевые, нечеткие и модели на основе методов сглаживания. Фундаментальной проблемой является проблема моделирования динамических процессов, порождающих временные ряды, особенностью которых является высокая степень неопределенности, которая выражается в: неопределенности значений – гетерогенном характере значений (количественном и качественном); неопределенности длины – вариабельности длины временных рядов от очень коротких до длинных; неопределенности поведения – нестационарном поведении ВР [26].

В современных условиях развития горнодобывающей отрасли растет роль средств, обеспечивающих и влияющих на скорость принятия решения, эти тенденции уже затронули практически все сферы деятельности и проникают в прикладные области в виде систем искусственного интеллекта [27]. Искусственные нейронные сети (ИНС) впервые появились в 1980-х годах как новое направление в разработке искусственного интеллекта (ИИ) и с тех пор успешно применяются для моделирования сложных задач.

Области применения нейронных сетей обширны – автоматизация процессов распознавания образов, прогнозирование, адаптивное управление, создание экспертных систем, организация ассоциативной памяти, обработка аналоговых и цифровых сигналов, синтез и идентификация электронных цепей и систем. Использование нейронных сетей в технологии интеллектуального анализа данных является актуальным направлением, которое непрерывно развивается. Все ИНС являются совокупностью двух типов элементов – нейронов и связей между ними. Нейроны представляют собой простые процессоры, вычислительные возможности которых ограничиваются некоторым правилом комбинаторики входных сигналов и правилом активации, позволяющим вычислить выходной сигнал по совокупности входных сигналов. Выходной сигнал элемента посылается другим элементам по взвешенным связям, с каждой из которых связан весовой коэффициент.

В зависимости от его значения передаваемый сигнал или усиливается, или подавляется. В целом работа с ИНС состоит из двух процедур: обучения и непосредственного решения поставленной задачи. Анализ данных (data mining), основанный на нечеткой нейронной сети. Основная идея, положенная в основу нечетких нейронных сетей, следующая: используется выборка данных для определения параметров функций принадлежности, которые лучше всего соответствуют некоторой системе логического вывода, то есть выводы делаются на основе аппарата нечеткой логики, а для нахождения параметров функций принадлежности используются алгоритмы обучения нейронных сетей. Такие системы могут использовать заранее известную информацию, обучаться, приобретать новые знания, прогнозировать временные ряды, выполнять классификацию образов и, кроме этого, они являются вполне наглядными для пользователя.

Результаты

В соответствии с этапами выбранного метода исследований F-AHP нами выполнены расчеты по определению весовых коэффициентов параметров и показателей для создания математического описания анализа грансостава развала. Для проведения исследований были выбраны 7 экспертов, методом анкетирования выполнена оценка параметров и показателей с использованием лингвистических переменных и треугольных нечетких чисел, по результатам оценки экспертов составлены матрицы нечетких агрегированных оценок параметров и показателей.

 Таблица 1 Разнородные параметры и показатели для создания математического описания

Table 1 Various parameters and indicators for creating a mathematical description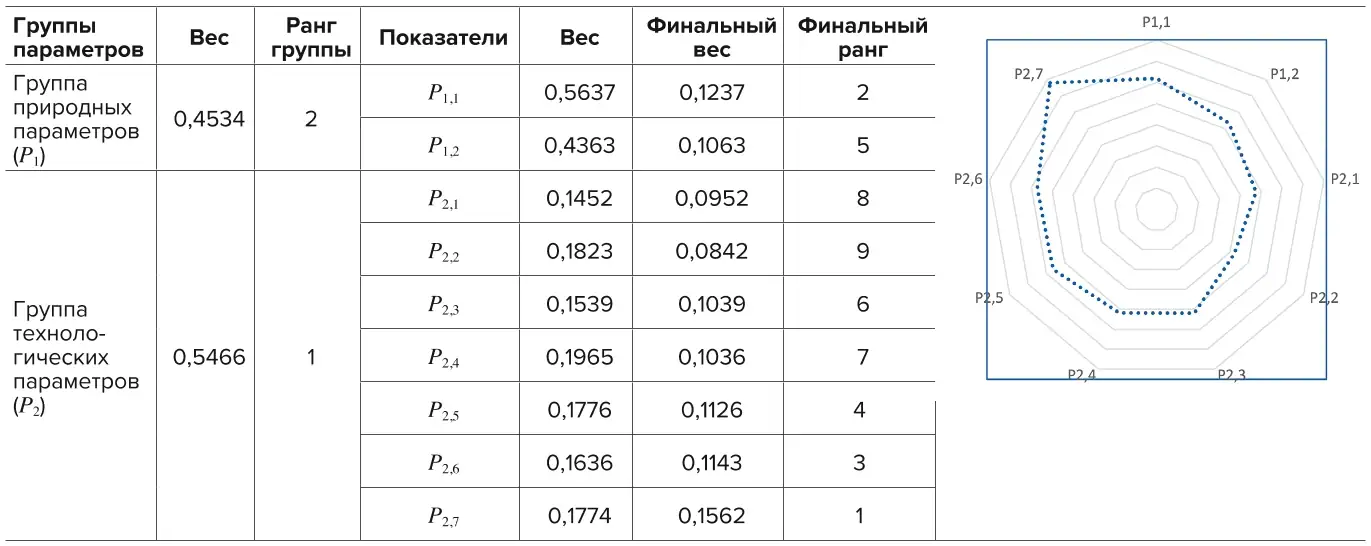

Итоговые результаты ранжирования процесса поэтапной обработки полученной информации методом F-AHP приведены в табл. 2, промежуточные данные в силу ограниченного объема публикации авторами не представлены. Исследование решения задач прогнозирования методами нейросетевого анализа предлагается проводить согласно следующей последовательности.

1. Физическая постановка задачи с целью построения обучающих выборок. Основой для создания обучающих выборок могут быть базы данных, содержащие аналитическую информацию по гранулометрическому составу пород на различных месторождениях твердых полезных ископаемых, с различными физико-механическими характеристиками пород, часть статистического материала для обработки использована из научно-технических источников, представленных в библиографическом списке, другая – данные по грансоставу с карьеров Уральского федерального округа.

2. Выбор архитектуры, топологии сети, а также выбор алгоритма ее обучения. Предварительная обработка данных и построение обучающих выборок.

3. Обучение, тестирование и возможное «дообучение» сети.

4. Анализ полученных результатов.

Используя основные положения теории НЛ, данные должны быть представлены в виде функций принадлежности. Данный этап называется фаззификацией, которая представляет собой процедуру нахождения значений функций принадлежности входных лингвистических переменных на основе обычных (не нечетких) исходных данных [20–22].

Для построения модели необходимо определить функции принадлежности каждого параметра μ(P1,1), μ (P1,2), …, μ (P2,7), а также построить нечеткую базу правил. Для фаззиидентификации привлекаются эксперты (10 человек, средний опыт работы 27,4 года). Экспертными методами определены терм-множества и функции принадлежности всех лингвистических переменных (рис. 2).

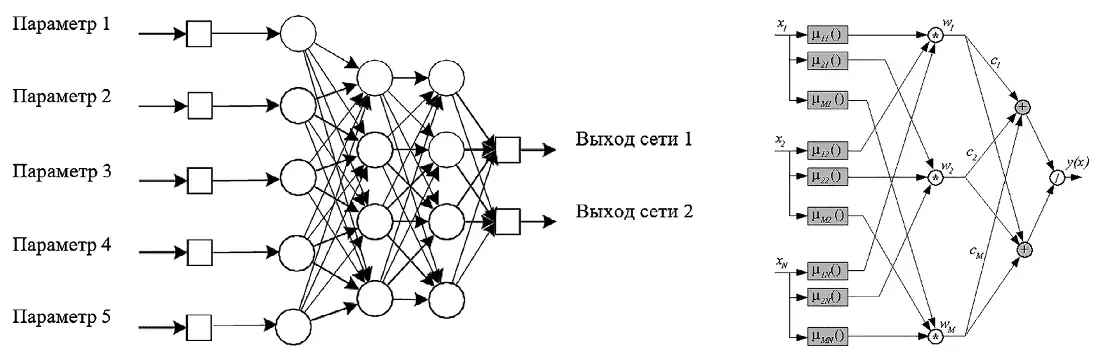 Рис. 2 ИНС прогнозирования грансостава в условиях малого объема достоверных исходных данных и неопределенности

Fig. 2 Forecasting of particle size distribution using an Artificial Neural Network in conditions of uncertainty and little reliable input data

При исследовании представленной ИНС точность результатов модели была подтверждена путем сопоставления прогноза с фактическими данными о фракционности в развале горных пород. Относительная погрешность модели составила менее 3% во всех исследованиях.

На рис. 3 представлена реализация гранулометрического анализа развала горной массы с использованием разработки ООО «Давтех». Обработка изображений развала горной массы с использованием ПАК разработки компании ООО «ДАВТЕХ» осуществлена на одном из действующих карьеров Уральского федерального округа.

 Рис. 3 Реализация анализа гранулометрического состава развала горной массы с использованием мобильного ПАК разработки компании ООО «ДАВТЕХ»

Fig. 3 Performing analysis of the particle size distribution of the rocks in the muck pile using mobile software and hardware suite developed by DAVTECH LLC

Заключение

Таким образом, в работе реализован оригинальный подход в решении многокритериальной задачи анализа и прогнозирования гранулометрического состава взорванных горных пород, учитывающий взаимовлияние значимых факторов и позволяющий объединить в одной модели разнородные параметры и показатели. Кроме того, решение задачи распознавания изображений развала горной массы в большой мере зависит от выбора исходного описания объекта исследований (грансостав развала), т. е. «пространства» параметров, показателей и признаков. При обоснованном выборе задача распознавания может оказаться тривиальной и, наоборот, неудачно выбранное «пространство» признаков способно привести либо к очень сложной обработке информации, либо вообще к отсутствию решения. Процедура поиска решения научно-практической задачи с использованием ИНС, прошедшей обучение, оказывается более гибкой, чем процесс программирования, поскольку ИНС может повышать точность результатов по мере накопления ею опыта и адаптироваться к происходящим изменениям.

Список литературы

1. Дремин А.В., Великанов В.С. К вопросу о гранулометрическом составе взорванных скальных пород. Горная промышленность. 2023;(4):73–78. https://doi.org/10.30686/1609-9192-2023-4-73-78

2. Панишев С.В., Ермаков С.А., Алькова Е.Л. О влиянии гранулометрии взорванного массива многолетнемерзлых пород на производительность драглайна. Горный информационно-аналитический бюллетень. 2011;(9):93–98. Режим доступа: https://giabonline.ru/files/Data/2011/9/Panishev_2011_9.pdf

3. Орынбай А. А. Разработка инновационных методов автоматизированного определения структурных характеристик взорванных горных пород на основе информационных технологий: дис. ... д-ра философии. Алматы; 2022. 130 с. Режим доступа: https://official.satbayev.university/download/documentPhd/26576/Диссертация%20PhD%20Орынбай%20АА.pdf

4. Саадун А., Фредж М., Букарм Р., Хаджи Р. Анализ дробления с использованием цифровой обработки изображений и эмпирической модели (Kuz-Ram): сравнительное исследование. Записки Горного института. 2022;257:822–832. https://doi.org/10.31897/PMI.2022.84

5. Salmi E.F., Sellers E.J. A review of the methods to incorporate the geological and geotechnical characteristics of rock masses in blastability assessments for selective blast design. Engineering Geology. 2021;281:105970. https://doi.org/10.1016/j.enggeo.2020.105970

6. Гундин А.А., Гундина М.А., Чешкин А.Н. Обработка цифровых изображений при дефектоскопии поверхностей промышленных объектов. Наука и техника. 2016;15(3):225–232. Режим доступа: https://rep.bntu.by/bitstream/handle/data/23909/225-232.pdf

7. Singh B.K., Mondal D., Shahid M., Saxena A., Roy P.N.S. Application of digital image analysis for monitoring the behavior of factors that control the rock fragmentation in opencast bench blasting: A case study conducted over four opencast coal mines of the Talcher Coalfields, India. Journal of Sustainable Mining. 2019;18(4):247–256. https://doi.org/10.1016/j.jsm.2019.08.003

8. Xie C., Nguyen H., Bui X-N., Choi Y., Zhou J., Nguyen-Trang T. Predicting rock size distribution in mine blasting using various novel soft computing models based on meta-heuristics and machine learning algorithms. Geoscience Frontiers. 2020;12(3):101108. https://doi.org/10.1016/j.gsf.2020.11.005

9. Dhekne P.Y., Balakrishnan V., Jade R.K. Effect of type of explosive and blast hole diameter on boulder count in limestone quarry blasting. Geotechnical and Geological Engineering. 2020;38:4091–4097. https://doi.org/10.1007/s10706-020-01280-y

10. Siddiqui F.I., Ali Shah S.M., Behan M.Y. Measurement of size distribution of blasted rock using digital image processing. Journal of King Abdulaziz University Engineering Sciences. 2009;20(2):81–93. https://doi.org/10.4197/Eng.20-2.4

11. Sudhakar J., Adhikari G.R., Gupta R.N. Comparison of fragmentation measurements by photographic and image analysis. Techniques Rock Mechanics and Rock Engineering. 2006;39(2):159–168. https://doi.org/10.1007/s00603-005-0044-9

12. Júlio de C.S., Andrêvhity da C.S., Suelen S.R. Analysis of blasting rocks prediction and rock fragmentation results using split-desktop software. Tecnologia em Metalurgia, Materiais e Mineração. 2018;15(1):22–30. https://doi.org/10.4322/2176-1523.1234

13. Tosun A. A modified Wipfrag program for determining muckpile fragmentation. Journal of the Southern African Institute of Mining and Metallurgy. 2018;118(10):1113–1199. https://doi.org/10.17159/2411-9717/2018/v118n10a13

14. Elahi A.T., Hosseini M. Analysis of blasted rocks fragmentation using digital image processing (case study: limestone quarry of Abyek Cement Company). International Journal of Geo-Engineering. 2017;8:16. https://doi.org/10.1186/s40703-017-0053-z

15. Souza J., Silva A., Rocha S. Analysis of blasting rocks prediction and rock fragmentation results using split-desktop software. Tecnologia em Metalurgia, Materiais e Mineração. 2018;15(1):22–30. https://doi.org/10.4322/2176-1523.1234

16. Осинцев Н.А. Многокритериальные методы принятия решений в «зелёной» логистике. Мир транспорта. 2021;19(5):105–114. https://doi.org/10.30932/1992-3252-2021-19-5-13

17. Осинцев Н.А., Рахмангулов А.Н., Сладковский А.В. Ранжирование инструментов зеленой логистики комбинированным методом Fuzzy AHP-TOPSIS. Транспорт Урала. 2020;(1):3–14. https://doi.org/10.20291/1815-9400-2020-1-3-14

18. Бурмистров К.В., Осинцев Н.А. Ранжирование параметров и показателей устойчивого функционирования и развития системы вскрытия карьера методом fuzzy AHP. Устойчивое развитие горных территорий. 2020;12(3):394–409. https://doi.org/10.21177/1998-4502-2020-12-3-394-409

19. Великанов В.С. Повышение эффективности эксплуатации карьерных гусеничных экскаваторов с оборудованием «прямая механическая лопата»: автореф. дис. … канд. техн. наук. Екатеринбург; 2009. 18 с.

20. Великанов В.С., Олизаренко В.В. К вопросу ранжирования профессиональных навыков машиниста карьерных экскаваторов. Горный информационно-аналитический бюллетень. 2010;(3):315–319. Режим доступа: https://giab-online.ru/files/Data/2010/3/ Velikanov_3_2010.pdf

21. Великанов В.С., Шабанов А.А. Метод анализа иерархий в установлении значений весовых коэффициентов эргономических показателей карьерных экскаваторов. В кн.: Социально-экономические и экологические проблемы горной промышленности, строительства и энергетики: 8-я Междунар. конф. по проблемам горной промышленности, строительства и энергетики, Тула, 1–2 нояб. 2012 г. Тула: Тульский государственный университет; 2012. Т. 1. С. 238–244.

22. Великанов В.С., Усов И.Г., Абдрахманов А.А., Усов И.И. Моделирование и оптимизация режимов работы горных машин с использованием среды MATLAB. Горный журнал. 2017;(12):78–81. https://doi.org/10.17580/gzh.2017.12.15

23. Ткаченко М.Г. Прогнозирование оставшегося времени безаварийной работы нефтегазодобывающего оборудования с применением технологии искусственных нейронных сетей. Инженерный вестник Дона. 2014;(4-1):21. Режим доступа: http://www. ivdon.ru/uploads/article/pdf/IVD_25_tkachenko.pdf_fb60339328.pdf

24. Elattar H.M., Elminir H.K., Riad A.M. Prognostics: a literature review. Complex & Intelligent Systems. 2016;2(2):125–154. https://doi.org/10.1007/s40747-016-0019-3

25. Heng A., Zhang S., Tan A.С.С., Matwew J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mechanical Systems and Signal Processing. 2008;23(3):724–739. https://doi.org/10.1016/j.ymssp.2008.06.009

26. Гришин И.А., Великанов В.С., Назаров О.В., Дерина Н.В. О возможности использования метода локальной аппроксимации для прогноза нерегулярных временных рядов отказов горнотранспортных машин. Уголь. 2022;(3):84–89. https://doi.org/10.18796/0041-5790-2022-3-84-89

27. Сергунин М.П., Еременко В.А. Обработка структурных геологических моделей алгоритмами искусственного интеллекта. Горный информационно-аналитический бюллетень. 2023;(9):56–67. https://doi.org/10.25018/0236_1493_2023_9_0_56