Анализ внезапного выброса газоугольной смеси из полости конической формы, сформированной в процессе выброса

С.В. Черданцев , П.А. Шлапаков, К.С. Лебедев
АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли», г. Кемерово, Российская Федерация
Горная Промышленность №6 / 2023 стр. 109-115

Резюме: Непременными атрибутами при добыче угля подземным способом являются метан и угольная пыль различной дисперсности. При их смешивании образуются газоугольные смеси, предрасположенные к различным опасным и особо опасным газодинамическим явлениям, в первую очередь к внезапным выбросам, сопровождающимся образованием полостей в угольном массиве и интенсивным выделением из них газоугольных смесей в выработки. В статье рассматривается задача об одномерном стационарном течении газоугольной смеси в подземной полости конусообразной формы, образующейся в процессе внезапного выброса. В качестве базовых уравнений используются уравнение движения Эйлера и уравнение неразрывности. В результате их преобразования получено обыкновенное дифференциальное уравнение первого порядка, для которого сформулирована задача Коши. Решением задачи Коши является трансцендентное уравнение относительно искомых чисел Маха. Корни трансцендентного уравнения вычислены с помощью математического программного пакета MathCAD. После нахождения чисел Маха определены остальные параметры смеси: давление, плотность и температура газоугольной смеси в любой точке конической области, включая их критические значения. Построены графики, на основе которых установлены некоторые закономерности одномерного стационарного течения газоугольной смеси в конической области. В частности, выявлено, что с ростом числа Маха параметры газоугольной смеси нелинейно уменьшаются, а с увеличением показателя адиабаты Пуассона давление и температура уменьшаются, а плотность увеличивается.

Ключевые слова: горные выработки, угольный пласт, внезапные выбросы, газоугольные смеси, уравнения газовой динамики, число Маха, критические параметры

Для цитирования: Черданцев С.В., Шлапаков П.А., Лебедев К.С. Анализ внезапного выброса газоугольной смеси из полости конической формы, сформированной в процессе выброса. Горная промышленность. 2023;(6):109–115. https://doi.org/10.30686/1609-9192-2023-6-109-115

Информация о статье

Поступила в редакцию: 21.09.2023

Поступила после рецензирования: 24.10.2023

Принята к публикации: 03.11.2023

Информация об авторах

Черданцев Сергей Васильевич – доктор технических наук, главный научный сотрудник, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), г. Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Шлапаков Павел Александрович – кандидат технических наук, заведующий лабораторией, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), г. Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Лебедев Кирилл Сергеевич – старший научный сотрудник, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), г. Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

Внезапные выбросы угля и газа в угольных шахтах происходят в течение многих десятилетий, практически во всех угледобывающих странах [1]. За этот период времени были накоплены и систематизированы многочисленные факты реализации внезапных выбросов. Однако к настоящему времени пока не создана единая теория внезапных выбросов угля и газа, описывающая их причинно-следственные связи протекания с единых методологических позиций.

Дело в том, что механизм внезапных выбросов очень сложен и обусловлен целым рядом сопряженных между собой явлений и факторов. По мнению ряда авторов [1–3], для корректного описания процесса внезапного выброса необходимо совместно сформулировать и найти решения, по крайней мере, трех задач. Первая из этих задач описывает фильтрацию газа в угольном пласте, вторая – рассматривает напряженно-деформированное состояние пласта, его разрушение вблизи забоя и образование подземных полостей и каверн. И, наконец, третья задача описывает особенности течения газоугольного потока в образовавшейся полости и его последующего выброса. Особо отметим, что все эти задачи тесно связаны между собой.

В первую очередь необходимо учесть, что непосредственно перед выбросом угольный пласт в краевой части вследствие процессов разрушения и трещинообразования значительно увеличивает свою проницаемость. В этом случае формируется мощный фильтрационный поток свободного газа, содержащегося в порах и трещинах, направленный из пласта к угольному обнажению, а затем в горную выработку. Таким образом, чтобы установить параметры фильтрационного потока перед выбросом необходимо определить параметры трещиноватости в краевой части разрушающегося пласта. К сказанному добавим, что форму и размеры образующейся в результате выброса полости можно установить только в результате решения второй задачи о напряженно-деформированном состоянии пласта и лишь после этого можно рассмотреть третью задачу о течении газоугольного потока внутри полости.

Обратим внимание, что все три указанные задачи в едином комплексе еще не обсуждались, ввиду очевидной сложности. Однако следует отметить ряд работ, которые внесли существенный вклад в решение каждой из этих задач.

Так, в статьях [4; 5] рассматриваются различные подходы к решению первой задачи. В частности, в статье [4] для описания геомеханических и физико-химических процессов в многофазных угольных пластах представлено так называемое аналитическое «операторное продолжение», связывающее между собой уравнение Ленгмюра и кинематическое уравнение для волн маятникового типа в напряженных геосредах. В статье [5] обсуждается математическая модель для описания фильтрации и диффузии свободного и сорбированного газа в угольном пласте. Рассмотрены ее асимптотические варианты, рассматривающие равновесное движение газа в порах при разных видах изотермы сорбции.

В рамках решения второй задачи отметим работы [6–8]. Например, в работе [6] показано, что выброс угля и газа осуществляется за счет энергии первоначально сжатого газа, заполняющего пространство между нераздробленными частицами угля и энергии сорбированного газа, способного к быстрому выделению из разрушенного угля. А в работах [7; 8] рассмотрена математическая модель породоугольного массива, предрасположенного к внезапному выбросу. За критерий выброса угля и газа принято условие, при котором не выполняется равновесие части пласта, находящейся под действием давления метана и сил трения между угольным пластом и «слабым» слоем, критическая длина которого вычислена в работе [8].

Третья задача обсуждалась в работах [9–12]. В работах [9; 10] показано, что если подземная полость состоит из сужающейся и расширяющейся частей, то выброс газа из подземной полости может произойти со сверхзвуковой скоростью и образованием ударной волны в выработке [11]. В работе [12] показано, что объемная доля пылевидного угля в двухфазном потоке является существенным фактором, влияющим на процесс затухания ударной волны, обусловленной внезапным выбросом.

В данной статье обсуждается третья задача о внезапных выбросах в рамках следующих допущений:

1) течение газоугольной смеси мы полагаем одномерным и стационарным;

2) если частицы угля пылевидные, то ввиду их малости мы пренебрегаем весом частиц и полагаем, что они и дальше будут двигаться со скоростью газового потока. Если же угольные частицы достаточно крупные, то кроме аэродинамических сил, на них действует сила тяжести, которая тормозит движение крупных частиц и быстро их останавливает, в то время как процесс истечения газа и пылевидных угольных частиц из полости продолжается еще некоторое время;

3) поскольку в работе рассматриваются только пылевидные частицы, то на основании второго допущения вместо двухкомпонентной смеси мы будем рассматривать однокомпонентную смесь, в силу чего газоугольную смесь будем полагать идеальным, политропным газом.

Из второго допущения следует, что количество выброшенного угля составляет лишь часть от массы всего угля в зоне отжима, а количество выброшенного газа определяется его содержанием во всей зоне отжима, из которой он выйдет полностью за определенный промежуток времени. Поэтому объем газа значительно превышает объем крупных угольных частиц.

Анализ форм подземных полостей и каверн, представленных в монографии [1], позволяет аппроксимировать некоторые виды подземных полостей совокупностью двухтрех геометрических фигур. В этой связи в данной статье подземная полость, образующаяся в результате выброса, рассматривается как область, состоящая из двух частей, одна из которых имеет форму, близкую к полусфере, а вторая представляет собой круговой усеченный конус (рис. 1). В процессе построения расчетной модели будем использовать аналогию между течением газа в подземной полости и течением в конфузоре энергетического сопла [13–15].

Постановка задачи о течении газоугольной смеси внутри подземной полости

На основании первого и третьего допущений для описания течения газоугольной смеси внутри подземной полости воспользуемся уравнением движения Эйлера и уравнением неразрывности. При стационарном, одномерном течении газа уравнение Эйлера имеет вид [13–15]

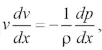(1)

где v, ρ, p – скорость, плотность и давление газоугольной смеси в полости; х – декартовая координата (см. рис. 1).

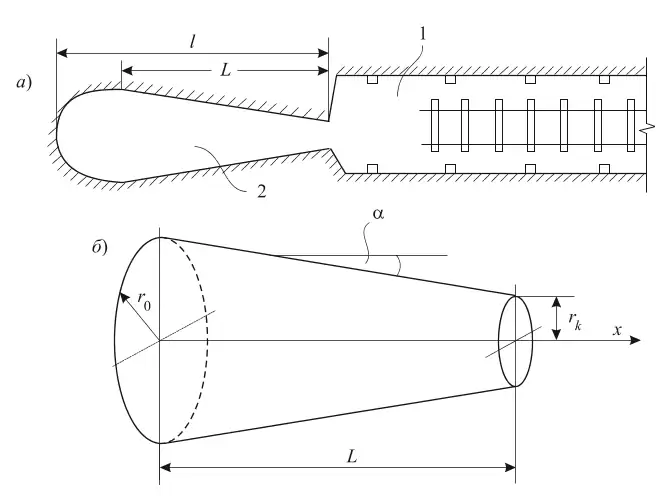Рис. 1 Форма подземной полости, образовавшейся при внезапном выбросе угля и газа: 1 – горная выработка, 2 – подземная полость

Fig. 1 The shape of the underground cavity formed by sudden coal and gas release: 1 – a mine workings, 2 – an underground cavity

Уравнение неразрывности запишем в следующем виде [13–15]:

(2)

где S – площадь произвольного поперечного сечения полости, координата которого х.

Продифференцировав уравнение (2) по х и подставив в уравнение (1), имеем

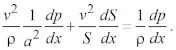(3)

В формуле (4), (3) величина a – является скоростью звука в газе, определяемая как [13]

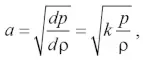(4)

где k – показатель адиабаты Пуассона. Поскольку величина M = v/a является числом Маха, то равенство (3) сначала преобразуем к виду

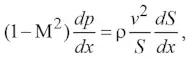(5)

а затем с помощью (1) получим соотношение

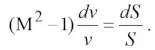(6)

Отметим, что уравнение (1) устанавливает зависимость между производными dv/dx и dp/dx, уравнение (5) связывает между собой производные dp/dx и dS/dx, а уравнение (6) устанавливает связь между dv/v и dS/S. Из анализа этих уравнений вытекают следующие выводы.

1. Если число Маха M < 1, то 1 – M² > 0, и поэтому из уравнения (5) следует, что знаки производных dp/dx и dS/dx совпадают. Следовательно, если сечение полости S сужается (dS/dx < 0), то давление газоугольной смеси падает (dp/dx < 0), а скорость, как это следует из уравнения (1), увеличивается (dv/dx > 0). Если же площадь S увеличивается (dS/dx > 0), то давление р тоже возрастает (dp/dx > 0), а скорость v уменьшается (dv/dx < 0).

2. Если M < 1, то величина 1 – M² < 0, и, следовательно, знаки производных dp/dx и dS/dx будут противоположными. В силу этого, если сечение уменьшается (dS/dx < 0), то давление возрастает (dp/dx > 0), а скорость уменьшается (dv/dx < 0). Если же площадь увеличивается (dS/dx > 0), то давление падает (dp/dx < 0), а скорость – увеличивается (dv/dx > 0).

3. Если M = 1, то 1 – M² = 0, и из уравнения (5) следует, что в некоторой точке x производная dS/dx = 0, и поэтому площадь сечения S в этой точке имеет экстремальное значение.

Из уравнения (6) следует, что если M < 1, то приращение скорости потока сопровождается уменьшением площади полости, а при M > 1, наоборот, рост скорости потока возможен только при увеличении сечения полости. Поэтому в точке x = xkp значение площади сечения полости должно быть минимальным – S = Smin. При этом условии скорость газоугольного потока в точке x = xkp становится равной скорости звука (M = 1), в связи с чем ее называют критической скоростью v = vkp = akp, а сечение Smin называют соответственно критическим сечением Skp.

Таким образом, чтобы получить сверхзвуковую скорость смеси, необходимо наличие в подземной полости трех элементов: суживающейся части (конфузора), горловины, в которой площадь S = S_min, и расширяющейся части (диффузора). Именно так и устроены энергетические сопла, предназначенные для получения потоков со сверхзвуковыми скоростями [13–15].

Решение задачи о течении газоугольной смеси внутри подземной полости конической формы

Для получения количественных оценок воспользуемся уравнением Бернулли [13]

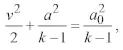(7)

где a₀ – скорость звука в покоящемся газе. Продифференцировав уравнение (7) и выполнив преобразования, получим равенство

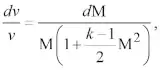(8)

связывающее скорость течения газа с числом Маха и показателем адиабаты Пуассона.

Найденное из формулы (8) отношение dv/v подставляем в (6) и после преобразования приходим к дифференциальному уравнению

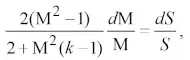(9)

в котором переменные разделены. Поскольку область течения газоугольной смеси представляет собой круговой усеченный конус, то

,

и тогда уравнение (9) приводится к виду

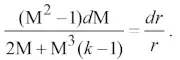(10)

Если на выходе смеси из конической полости M = 1, то имеет место следующее условие:

(11)

где r_k – радиус малого поперечного сечения конической полости.

Условие (11) можно рассматривать в качестве граничного условия для уравнения (10), в силу чего уравнение (10) и граничное условие (11) представляют собой задачу Коши. Поскольку в уравнении (10) переменные разделены, то, интегрируя его и учитывая условие (11), имеем

(12)

Подставляя условие (11) в (12), придем к уравнению

,

из которого находим постоянную интегрирования

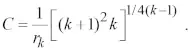(13)

Поскольку полость имеет форму усеченного конуса, то между текущим радиусом поперечного сечения r и координатой x имеет место следующее соотношение:

(14)

содержащее радиус выходного сечения полости rk, ее длину L и угол конусности α.

Подставив формулу (14) в равенство (12), получим уравнение

(15)

левая часть которого зависит только от числа Маха, а правая – только от координаты x. Поэтому для отыскания решения уравнения (15) мы поступим следующим образом. Вначале вычислим в ряде точек x = 0, 1, 2, … 10 м значения функции

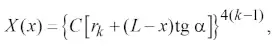(16)

представляющей собой правую часть уравнения (15). Затем, подставив найденные значения X(x) в (15), получим уравнение

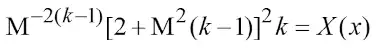(17)

относительного искомого числа Маха. Количество уравнений (17) соответствует количеству выбранных точек x. Поскольку уравнение (17) трансцендентное, то найти его решение в замкнутом виде невозможно. Поэтому в данной работе использовался математический программный пакет MathCAD, в котором решение уравнения найдено численно с использованием связки функций Given–Find. Так, например, при k = 1,4; α = 5°; rk = 0,5 м; L = 10 м числа Маха, найденные из уравнения (17) в точках x = 0; 2; 8 м, оказались равными соответственно M = 0,084; 0,111; 0,373. Чтобы найти давление, плотность, температуру и скорость газоугольной смеси, воспользуемся уравнением Бернулли (7), из которого с помощью формулы (4), получим соотношение

(18)

Поскольку согласно четвертому допущению газ политропный, то, учитывая формулу адиабаты Пуассона [13]

(19)

где D – некоторая постоянная величина, после преобразования сначала получим формулу для определения давления газоугольной смеси в конической части подземной полости

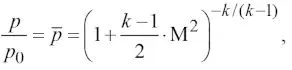(20)

а затем и формулу для плотности газа

(21)

Учитывая уравнение Менделеева–Клапейрона и принимая во внимание, что скорость звука в газе может быть определена по формуле , находим относительную температуру газоугольной смеси

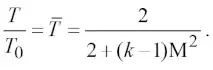(22)

Из уравнения Бернулли и формул (20), (21) нетрудно получить формулу для скорости истечения газа из подземной полости

(23)

где – скорость газоугольной смеси, отнесенная к скорости звука в покоящемся газе a₀, т.е.

(24)

откуда получаем формулу

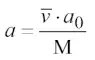(25)

для определения скорости звука a в произвольном сечении конической области.

Анализ полученных результатов

Вышеприведенные рассуждения позволяют нам составить алгоритм вычисления искомых параметров газоугольной смеси вдоль конической части подземной полости, который представляется в следующем виде. Вначале разбиваем длину L конической полости точками xi на n участков. В каждой точке x_i определяем значение функции X_(xi) по формуле (16), затем отыскиваем решение трансцендентного уравнения (17), корнями которого являются числа Маха M_i. Для каждого числа M_i по формулам (20) – (23), (25) вычисляем соответственно давление p_i, плотность ρ_i, температуру T_i, скорость v_i газоугольной смеси и скорость звука в ней a_i. По вычисленным значениям можно построить графики искомых параметров смеси.

В данной статье вычислительные процедуры выполнены при исходных данных, указанных ранее. На рис. 2 показаны графики некоторых параметров газоугольной смеси вдоль конической части подземной полости.

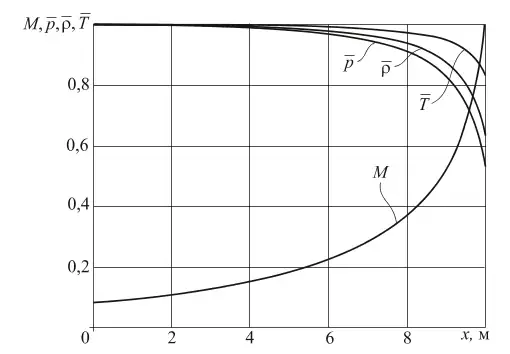Рис. 2 Распределение параметров газоугольной смеси вдоль продольной оси полости

Fig. 2 Distribution of the gas-coal mixture parameters along the longitudinal axis of the cavity

Анализируя представленные графики, замечаем, что на выходе из полости (в точке x = 10 м) число Маха достигает единицы и, следовательно, скорость газоугольной смеси имеет критическое значение. Функция M_(x) на рассматриваемом участке всюду монотонно растет, а ее график представляет собой сильно вогнутую кривую. Напротив, функции , на участке монотонно уменьшаются, особенно при значениях x > 8 м, а их графики являются выпуклыми кривыми.

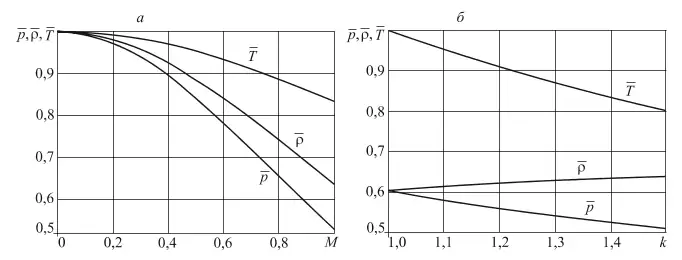Рис. 3 Графики зависимостей параметров смеси от числа Маха при k = 1,4 (а) и графики зависимостей параметров смеси от показателя адиабаты k при M = 1 (б)

Fig. 3 Graphs of the mixture parameters dependence on the Mach number at k = 1,4 (а) and graphs of the mixture parameters dependence on the adiabatic index k at M = 1 (б)

Обратим внимание, что искомые параметры газоугольной смеси являются функциями числа Маха и показателя адиабаты Пуассона. Их графики показаны на рис. 3, а и 3, б. Анализируя графики на рис. 3, а, замечаем, что они качественно схожи, поскольку на рассматриваемом отрезке все графики выпуклы и монотонно убывают, причем особенно интенсивно убывает функция , характеризующая давление газоугольной смеси. Графики функций , показанные на рис. 3, б, построены при M = 1. Анализ графиков показывает, что на рассматриваемом отрезке функция монотонно уменьшается, а ее график представляет собой прямую линию. Напротив, функция монотонно возрастает, но ее график также является прямой линией. График же функциипредставляет слабо вогнутую кривую, характеризующую монотонное убывание функции.

Приведенный анализ графиков на рис. 2, 3, а и 3, б показывает, что с увеличением числа Маха давление, плотность и температура газоугольной смеси нелинейно уменьшаются, причем особенно сильно – давление. С увеличением же показателя адиабаты Пуассона k уменьшаются только давление и температура, а плотность, наоборот, увеличивается.

Подставив в формулы (20) – (23) значение числа Маха M = 1, определим сначала критические параметры газоугольной смеси:

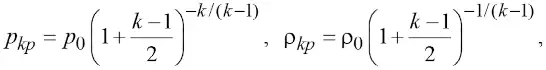
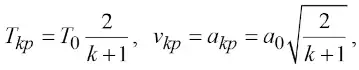
а затем по формуле (2) вычислим массу газоугольной смеси Qkp в процессе выброса из подземной полости в горную выработку

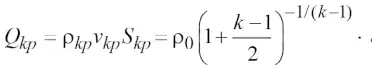
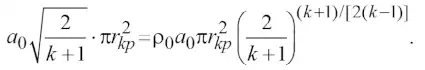(26)

Из формулы (26) видно, что масса смеси, выброшенной из подземной полости, зависит только от состояния смеси внутри полости и не зависит от параметров смеси вне полости.

Заключение

Основные результаты работы сводятся к следующему:

– сформулирована задача, описывающая одномерное, стационарное течение газоугольной смеси в подземной полости конической формы;

– в процессе построения решения сформулированной задачи получено трансцендентное уравнение относительно числа Маха, корни которого вычислены с помощью математического программного пакета MathCAD;

– найденные числа Маха позволили определить основные параметры газоугольной смеси: давление, плотность, температуру, в том числе и критические их значения;

– по вычисленным значениям параметров построены их графики вдоль продольной оси полости, а также в зависимости от значения числа Маха и показателя адиабаты Пуассона. Анализ графиков позволил установить:

а) числа Маха на участке всюду монотонно возрастают, а давление, плотность и температура, наоборот, монотонно уменьшаются, особенно заметно при x > 8 м;

б) с увеличением числа Маха давление, плотность и температура смеси нелинейно уменьшаются, причем особенно сильно уменьшается давление. С увеличением же показателя адиабаты Пуассона k уменьшаются только давление и температура, а плотность увеличивается.

Список литературы

1. Ходот В.В. Внезапные выбросы угля и газа. М.: Госгортехиздат; 1961. 363 с.

2. Христианович С.А. Распределение давления газа вблизи движущейся свободной поверхности угля. Известия АН СССР. 1953;(12):1673–1678.

3. Трофимов В.А. Внезапный выброс угля и газа. Вынос угля и газа в выработанное пространство. Горный информационноаналитический бюллетень. 2011;(S1):391–405.

4. Oparin V.N. Theoretical fundamentals to describe interaction of geomechanical and physicochemical processes in coal seams. Journal of Mining Science. 2018;53(2):201–215. https://doi.org/10.1134/S1062739117022031

5. Fedorov A.V., Fedorchenko I.A. Mathematical modeling of methane flow in coal beds. Journal of Mining Science. 2009;45(1):9–21. https://doi.org/10.1007/s10913-009-0002-0

6. Fedorov A.V. Shock wave in a coal bed under nonuniform desorption. Journal of Mining Science. 2014;50(1):38–42. https://doi.org/10.1134/S1062739114010062

7. Черданцев Н.В., Черданцев С.В., Зыков В.С. Моделирование геомеханического состояния породного массива, вмещающего выработку и дизъюнктивное нарушение. Маркшейдерский вестник. 2017;(3):51–55.

8. Черданцев Н.В. Результаты численного решения уравнений предельного состояния краевой зоны пласта и их аппроксимация полиномами. Безопасность труда в промышленности. 2019;(6):7–13. https://doi.org/10.24000/0409-2961-2019-6-7-13

9. Черданцев С.В., Черданцев Н.В., Ли Х.У., Лебедев К.С., Ли К.Х., Хаймин С.А. Определение параметров суфлярных выделений газа из угольного пласта в горные выработки. Вестник Научного центра по безопасности работ в угольной промышленности. 2017;(1):26–33.

10. Черданцев Н.В., Черданцев С.В., Ли Х.У., Филатов Ю.М., Шлапаков П.А., Лебедев К.С. Об одном подходе к описанию суфлярных выделений газа из резервуаров угольного массива в горные выработки. Безопасность труда в промышленности. 2017;(3):45–52. https://doi.org/10.24000/0409-2961-2017-3-45-52

11. Черданцев С.В., Шлапаков П.А., Потапов П.В., Голоскоков С.И., Лебедев К.С., Шлапаков Е.А. Математическое моделирование процесса формирования и выброса смеси «газ-уголь» в горные выработки. Вестник Научного центра ВостНИИ по промышленной и экологической безопасности. 2021;(3):40–52. https://doi.org/10.25558/VOSTNII.2021.31.51.005

12. Zhou A.T., Wang K., Oparin V.N. Regularities of two-phase gas flow under coal and gas outbursts in mines. Journal of Mining Science. 2018;53(3):533–543. https://doi.org/10.1134/S1062739117032476

13. Пирумов У.Г., Росляков Г.С. Газовая динамика сопел. М.: Наука; 1990. 368 с.

14. Ilakkiya S., Sridhar B.T.N. Study of decay, spread, and shock structure of a supersonic jet issuing from a C-D nozzle with semi-circular grooves. Thermophysics and Aeromechanics. 2022;29(3):327–346. https://doi.org/10.1134/S0869864322030027

15. Gromyko Yu.V., Tsyryulnikov I.S., Maslov A.A. Development of a method for determining flow parameters in impulse wind tunnels. Thermophysics and Aeromechanics. 2022;29(5):659–672. https://doi.org/10.1134/S0869864322050043