Самовоспламенение пылегазовоздушных смесей в атмосфере горных выработок

С.В. Черданцев , П.А. Шлапаков, К.С. Лебедев, А.Ю. Ерастов, С.А. Хаймин
АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли», г. Кемерово, Российская Федерация
Горная Промышленность №2 / 2024 стр. 121-126

Резюме: Разработка угольных месторождений подземным способом, как правило, сопровождается проявлением ряда негативных факторов, одним из которых является наличие пылегазовоздушных смесей, состоящих из мелкодисперсной угольной пыли, выделяющегося из разрушенного угля метана и воздуха рудничной атмосферы. Несмотря на современные методы и средства пылеподавления и пылеулавливания добиться полной нейтрализации пылегазовоздушных смесей в атмосфере горных выработок пока не удается. Негативное воздействие пылегазовоздушных смесей может проявляться по-разному. С одной стороны, отложения угольной пыли в выработанных пространствах при определенных условиях образуют очаги самовозгорания, являющиеся причинами эндогенных пожаров. С другой стороны, пылегазовоздушные смеси предрасположены к возгоранию от внешних источников или к самовоспламенению с последующим горением в форме дефлаграции, переходящей при определенных условиях в детонацию, распространяющуюся в атмосфере горных выработок со сверхзвуковой скоростью. В данной статье рассматривается нестационарная одномерная задача о самовоспламенении пылегазовоздушных смесей в воздушных потоках горных выработок. На основе решения данной задачи, построенного численно с помощью метода Гира, найдены температура и период самовоспламенения пылегазовоздушных смесей. Выполнен анализ процесса самовоспламенения смесей и выявлены некоторые закономерности влияния параметров смесей на период их самовоспламенения.

Ключевые слова: горные выработки, пылегазовоздушные смеси, уравнение баланса тепловой энергии, стехиометрическое соотношение, температура самовоспламенения, период самовоспламенения, адиабатический процесс

Для цитирования: Черданцев С.В., Шлапаков П.А., Лебедев К.С., Ерастов А.Ю., Хаймин С.А. Самовоспламенение пылегазовоздушных смесей в атмосфере горных выработок. Горная промышленность. 2024;(2):121–126. https://doi.org/10.30686/1609-9192-2024-2-121-126

Информация о статье

Поступила в редакцию: 17.02.2024

Поступила после рецензирования: 04.03.2024

Принята к публикации: 11.03.2024

Информация об авторах

Черданцев Сергей Васильевич – доктор технических наук, главный научный сотрудник, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Шлапаков Павел Александрович – кандидат технических наук, заведующий лабораторией, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Лебедев Кирилл Сергеевич – старший научный сотрудник, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Ерастов Антон Юрьевич – старший научный сотрудник, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Хаймин Сергей Александрович – старший научный сотрудник, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), Кемерово, Российская Федерация; е–mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

В процессе эксплуатации угольных шахт проявляется ряд негативных факторов, препятствующих ритмичной работе и безопасности угольных предприятий. Одним из основных негативных факторов является наличие пылегазовоздушных смесей, образующихся в атмосфере горных выработок при смешении метана, мелкодисперсной угольной пыли и рудничного воздуха [1].

В зоне действия рабочего органа угольного комбайна образующиеся пылегазовоздушные смеси частично нейтрализуются системами пылеподавления комбайна, а также обработкой смесей инертной пылью. Однако нейтрализация пылегазовоздушных смесей, как правило, не является полной, в связи с чем концентрация смесей в атмосфере очистных выработок остается достаточно высокой.

В естественных условиях в пылегазовоздушных смесях, как правило, отсутствуют процессы химического реагирования в течение длительного времени [2–4]. Но с повышением температуры пылегазовоздушные смеси способны реагировать с прогрессирующим нарастанием скорости реакции и переходом при определенных условиях в качественно новое состояние. Переход от состояния, при котором реагирование практически не происходит, к быстрой химической реакции с появлением пламени, как известно, называется самовоспламенением смеси [3; 4] и представляет собой процесс возникновения горения.

При самовоспламенении состав смеси изменяется только за счет протекания химических реакций. Температура же смеси изменяется скачкообразно вследствие преобладания тепловыделения над теплоотводом через боковую поверхность горной выработки, ограничивающей рассматриваемый объем пылегазовоздушной смеси [5]. Самовоспламенение пылегазовоздушной смеси в горной выработке происходит, как правило, при постоянном давлении [6].

Продолжительность времени, в течение которого самопроизвольное развитие процесса реагирования приводит к резкому подъему температуры, называется периодом самовоспламенения или периодом индукции [2–4]. Чем ниже начальная температура смеси, тем медленнее развивается процесс самовоспламенения.

Известно, что процесс воспламенения представляет собой в первую очередь химический процесс, сопровождающийся превращением веществ [2]. Однако, следует заметить, что этот процесс не происходит независимо, а обусловлен чисто физическими процессами, такими, как теплопроводность, диффузия, конвекция, излучение [3; 4; 6; 7]. Например, воспламенение может быть осуществлено в покоящемся облаке двухкомпонентной смеси [8], а также в ламинарном потоке при наличии внешнего источника зажигания или при наличии стационарного пламени [9; 10].

При высоких температурах покоящейся смеси ее самовоспламенение, как правило, завершается взрывом, а последующее за ним горение носит волновой характер [11; 12]. К сказанному добавим, что самовоспламенение является, вообще говоря, нестационарным процессом [6; 8].

Однако для упрощения задачи первоначально можно рассматривать стационарную теорию теплового самовоспламенения, в которой определяется критическое состояние смеси, являющееся предельным стационарным состоянием [13; 14]. Так как согласно стационарной теории в критическом состоянии выделяющееся тепло полностью отводится, то температуре самовоспламенения отвечает достаточно большая величина периода индукции.

Если период индукции мал, то необходимо пользоваться нестационарной теорией теплового самовоспламенения, поскольку в этом случае появляется возможность выявить динамику развития процесса самовоспламенения, а также влияние свойств топлива и физических условий на процесс самовоспламенения [6].

В данной статье рассматривается нестационарная задача о самовоспламенении пылегазовоздушных смесей в потоках горных выработок. Тематика данной статьи нам представляется достаточно актуальной, если учесть наличие в окрестности горных выработок очагов самонагревания, способных заметно увеличить температуру горных пород в окрестности горных выработок, что существенно повысит предрасположенность смесей к самовоспламенению. Использование нестационарной теории, на наш взгляд, позволит выявить динамику развития процесса самовоспламенения, а также влияние свойств смесей и физических условий на процесс самовоспламенения.

Нестационарную задачу о самовоспламенении смесей будем рассматривать в рамках следующих допущений:

1. горная выработка, внутри которой происходит химическое реагирование пылегазовоздушных смесей, имеет круглое поперечное сечение;

2. пылегазовоздушные смеси содержат только мелкодисперсные угольные частицы;

3. поток пылегазовоздушных смесей считаем одномерным;

4. размеры горной выработки, занятой пылегазовоздушной смесью, гораздо больше расстояний между угольными частицами, и поэтому смесь будем рассматривать как некоторую однородную среду;

5. лучистым теплообменом внутри зоны самовоспламенения пренебрегаем.

Постановка и решение задачи о самовоспламенении пылегазовоздушных смесей в атмосфере горных выработок

Пусть в атмосфере горной выработки со скоростью v движется поток пылегазовоздушной смеси, в которой происходит химическое реагирование, в результате чего выделяется тепловая энергия Qp. Часть тепловой энергии Qн расходуется на нагрев смеси, а другая часть Qт, отводимая через боковую поверхность выработки в массив горных пород, представляет собой потерю тепловой энергии. В силу сказанного тепловой баланс будет выражаться равенством [3; 4; 6]:

Q_p = Q_н – Q_т . (1)

Тепловую энергию Qp, выделяющуюся в результате химического реагирования, запишем в следующем виде [4; 6]:

Q_p = q · c · μ · S_Σ · k_T · M · k₀e ^–E/RT , (2)

где q – удельная теплота сгорания угольных частиц; c и μ – соответственно концентрация кислорода и угольной пыли в рассматриваемой области при 0°C и 760 мм рт. ст.; S_Σ – поверхность угольных частиц массой 1 кг; k₀ – предэкспоненциальный множитель; E – энергия активации; R – универсальная газовая постоянная; T – текущая температура смеси, K.

Поскольку концентрация угольных частиц и кислорода определяется экспериментально при 0°C, чему соответствует температура T = 273 K, то в формулу (2) введен коэффициент приведения k_T, равный

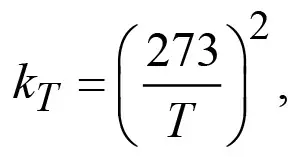(3)

который учитывает концентрацию угольных частиц и кислорода при текущей температуре T. Величина M, входящая в формулу (2), представляет собой стехиометрическое соотношение, показывающее отношение веса прореагировавшей угольной пыли G_T0 к весу израсходованного при этом кислорода G₀:

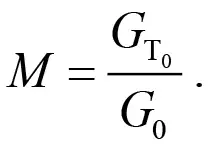(4)

Стехиометрическое соотношение определяется из рассмотрения химической реакции. Так, при протекании реакции полного выгорания углерода [2–4]

C+O₂=CO₂

теоретически необходимые количества угля и кислорода составляют G_T0 = 12 кг, G₀ = 32 кг и поэтому стехиометрическое соотношение (4) составляет M = 12/32 = 0,375.

Горению в гетерогенном режиме соответствуют две химические реакции [4]:

3C+2O₂=CO₂+2CO; 4C+3O₂=2CO₂ + 2CO,

откуда следует, что теоретически необходимое количество угля и кислорода в первой реакции составляет G_T0 = 36 кг, G₀ = 64 кг, а во второй реакции G_T0 = 48 кг, G₀ = 96 кг, в силу чего стехиометрические соотношения соответственно: M = 36/64 = 0,5625, M = 48/96 = 0,5. Низкотемпературное выгорание углерода, протекающее по схеме [4]

2C+O₂=2CO;

имеет G_T0 = 24 кг, G₀ = 32 кг и поэтому M = 24/32 = 0,75. При других режимах горения углерода величина стехиометрического соотношения, как показано в работах [4; 6], лежит в интервале M [0,375; 0,75].

Возвращаясь к уравнению теплового баланса (1), найдем расход тепла на нагрев смеси, используя формулу [3]

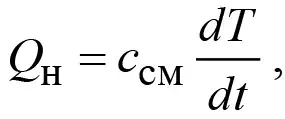(5)

где c_см – теплоемкость смеси при 0°C и 760 мм рт. ст.; t – время.

И, наконец, потери тепла Qт определим по формуле Ньютона [7]:

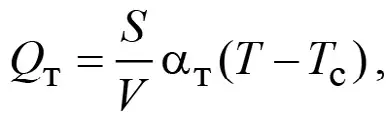(6)

где α_т – коэффициент теплообмена смеси с окружающим породоугольным массивом; T_c – температура боковой поверхности выработки; S и V – соответственно боковая поверхность и объем той части длины L горной выработки, в которой происходит химическое реагирование смеси. Поскольку выработка имеет круглое поперечное сечение диаметром D, то

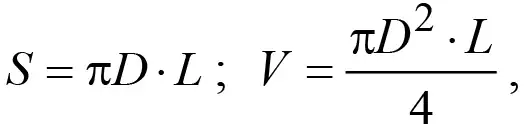
в связи с чем формулу (6) приведем к виду

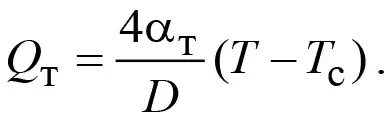(7)

Подставив формулы (2), (5) и (7) в уравнение (1), приходим к следующему дифференциальному уравнению:

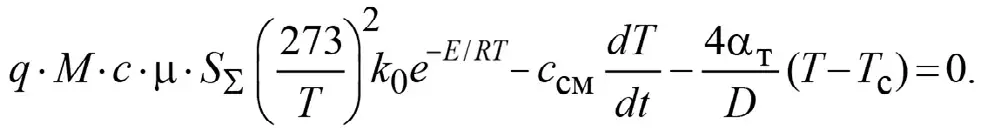(8)

Обозначив в уравнении (8) показатель степени как

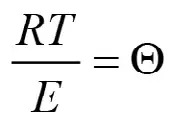(9)

и выразив из (9) температуру

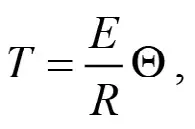(10)

преобразуем уравнение (8) следующим образом:

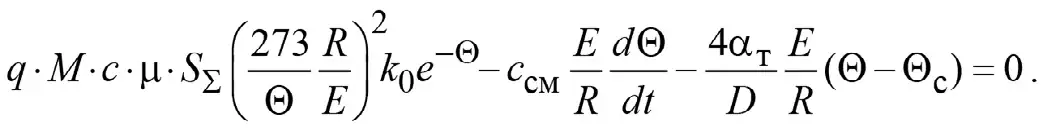
Полученное уравнение разделим на величину

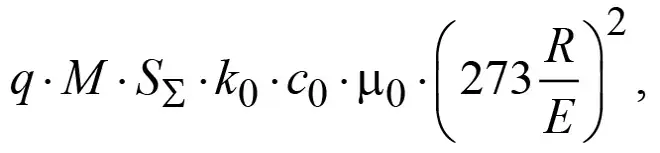
в силу чего оно преобразуется к виду

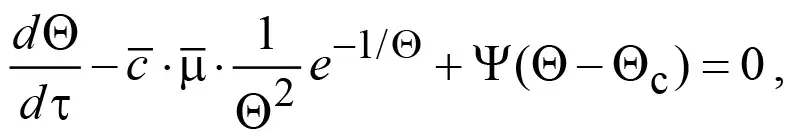(11)

где безразмерное время τ, безразмерный коэффициент теплоотдачи Ψ, безразмерные концентрации кислорода c и угольной пыли μ определены следующим образом:

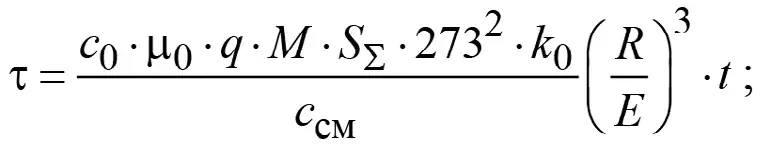(12)

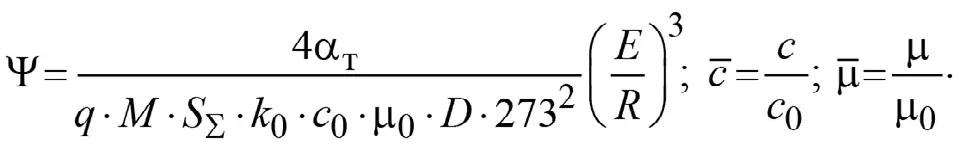(13)

Если полагать, что концентрации реагирующего газа c и угольной пыли μ изменяются в процессе химического реагирования, то уравнение (11) не определено, поскольку содержит кроме искомой безразмерной температуры Θ еще неизвестные величины c и μ. Поэтому для решения рассматриваемой здесь задачи необходимо в дополнение к уравнению (11) составить еще два уравнения, связывающие  c и μ с безразмерным временем τ.

Однако в этой статье мы учтем, что наиболее интенсивно концентрации реагирующего газа и угольной пыли изменяются в процессе распространения пламени, когда реагирующий газ и угольная пыль интенсивно выгорают. На начальном же этапе химического реагирования изменения концентраций и хотя и происходят, но несущественно. Поэтому в качестве дополнительного упрощения мы пренебрежем изменением концентраций и в рассматриваемом процессе и будем полагать, что  c = 1 и μ = 1.

В силу сказанного уравнение (11) приобретает следующий вид:

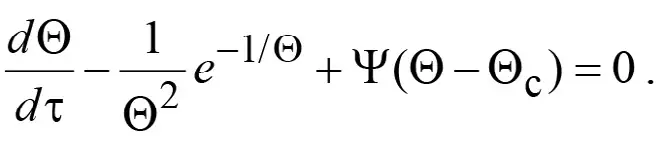(14)

Дифференциальное уравнение (14) описывает рассматриваемый процесс химического реагирования единственным образом только в том случае, если искомая функция Θ в начальный момент времени нам заранее известна. Иначе говоря, искомое решение уравнения (14) должно удовлетворять при τ = 0 некоторому начальному условию, которое в данном случае представляется в виде

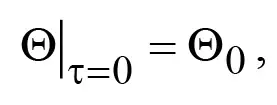(15)

где Θ₀ – известное значение искомой функции Θ в начальный момент времени.

Таким образом, дифференциальное уравнение (14) в совокупности с граничным условием (15) образует задачу Коши [15] для искомой функции Θ.

Уравнение (14) является нелинейным, поэтому найти его решение в квадратурах не представляется возможным [15]. В связи с этим в данной статье решение задачи Коши (14), (15) построено численно методом Гира [16] и реализовано с помощью программного пакета Maple V Power Edition [17].

В статье приняты следующие исходные данные, заимствованные из работ [2; 4; 6; 13]: D = 3 м; v = 5 м/с; c₀ = 0,23 кг/м³; μ₀ = 0,355 кг/м³; q = 27·106 Дж/(кг·K); M = 0,375; S_Σ = 1850 м²/кг; k₀ = 3,5·103 м/с; E = 133·103Дж/моль; T0 = 848 K; Tс = 848 K; cсм = 880 Дж/(кг·К); αТ = 15 Вт/(м²·К); R = 8,31 Дж/(моль·K). Подставляя исходные данные сначала в формулу (9), вычисляем Θ₀ = Θ_с = 0,0534, а затем по формуле (13) определяем Ψ = 2,052·10^-4.

Используя далее метод Гира и программный пакет Maple V численно находим решение Θ(τ) задачи Коши, график которого представлен на рис. 1 (линия 1).

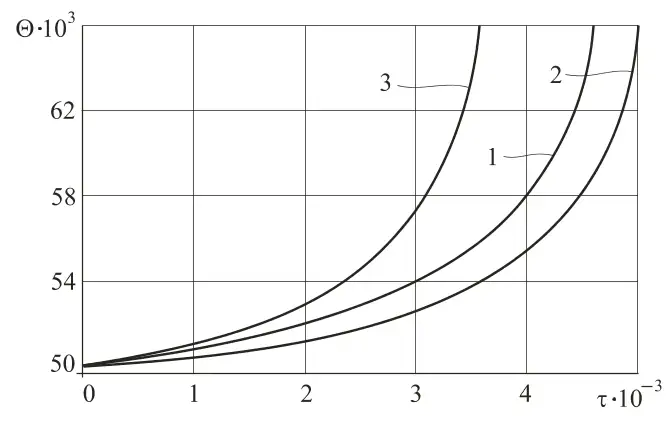
Анализ рис. 1 и полученных численных значений показывает, что на отрезке τ∈ [4600; 4620] происходит практически скачкообразный рост искомой функции Θ(τ), которая изменяется от значения Θ(4600) = 0,0663 до значения Θ(4620) = 2,466 и далее продолжает неограниченно расти.

Анализ полученных результатов

Известно, что если значение искомой функции скачкообразно и неограниченно увеличивается, то рассматриваемая физическая система неустойчива, поскольку находится в критическом состоянии. Это значит, что система способна перейти в новое состояние, качественно отличное от начального состояния [18].

Из сказанного следует, что скачкообразное изменение безразмерной температуры Θ(τ) представляет собой качественный переход от химического реагирования смеси, характеризуемого её разогревом, в новое состояние, при котором химическое реагирование сопровождается распространением пламени. Следовательно, точку τ_к1 = 4600 можно приближенно считать критической точкой, в которой происходит воспламенение пылегазовоздушной смеси, а значение искомой функции в критической точке является её критическим значением Θ_к(τ_к), которое в условиях рассматриваемого примера составляет Θ_к1 = 0,0663. Таким образом, безразмерное время τк представляет собой период самовоспламенения смеси, который также называют периодом индукции [6; 8–10].

В результате самовоспламенения в поперечном сечении выработки возникает фронт пламени, который может распространяться вдоль выработки в режиме дефлаграции либо в режиме детонации. В данной статье эти режимы не обсуждаются, поскольку они реализуются в закритической области (при τ > τ_к), что выходит за рамки постановки и решения задачи, рассматриваемой в данной статье.

Если в условиях рассматриваемого примера изменить только коэффициент теплообмена, увеличив его до α_Т = 20 Вт/(м²·К), то соответственно увеличится безразмерный коэффициент Ψ = 2,736·10^-4, что указывает на более интенсивный теплообмен с окружающим выработку породоугольным массивом. Полученное решение задачи Коши (14), (15) и его график на рис. 1 (линия 2) показывают качественное сходство искомой функции Θ(τ), построенной при различных значениях параметра Ψ. Разница заключается только в том, что с увеличением коэффициента теплообмена Ψ критическая точка τк удаляется от начала координат. Так, если при значении коэффициента теплообмена Ψ= 2,052·10^-4 критическая точка занимала положение τ_к1 = 4600, то при значении Ψ = 2,736·10^-4 критическая точка переместилась в положение τ_к2 = 5040, но при этом критическое значение функции Θ_к2 = 0,0663 не изменилось.

Таким образом, при увеличении теплообмена между пылегазовоздушной смесью и окружающим породоугольным массивом период воспламенения смеси возрастает, но температура воспламенения остается прежней.

Если же теплообмена между смесью и породоугольным массивом не происходит или он пренебрежимо мал, то в уравнении (14) коэффициент теплообмена Ψ = 0, в связи с чем уравнение (14) существенно упрощается:

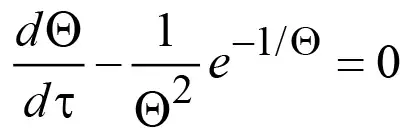(16)

и в совокупности с начальным условием (15) образует задачу Коши, которая описывает химическое реагирование пылегазовоздушной смеси в адиабатическом режиме, т.е. без теплообмена смеси с окружающим породоугольным массивом. Решение задачи Коши (16), (15) построено также методом Гира и показано на рис. 1 (график 3).

Анализируя рисунок, замечаем, что графики, описывающие химическое реагирование в адиабатическом процессе (график 3) и в условиях теплообмена с окружающим породоугольным массивом (графики 1 и 2), качественно схожи. Однако критическая точка τ_к3 = 3720 находится значительно ближе к началу координат, чем критические точки τ_к1, τ_к2. Следовательно, период времени, в течение которого происходит самовоспламенение смеси в условиях адиабатического процесса, существенно меньше периода воспламенения смеси при наличии теплообмена с окружающим массивом. Однако значение функции, как уже ранее отмечено, остается прежним, т.е. Θ_к3 = Θ_к2 = Θ_к1 = Θ_к = 0,0663.

Далее перейдем от безразмерных величин к размерным и определим критическую температуру, при которой происходит самовоспламенение, и периоды самовоспламенения, соответствующие различным критическим точкам. Для этого воспользуемся формулами (10) и (12).

Вначале из (10) определяем критическую температуру по шкале Кельвина:

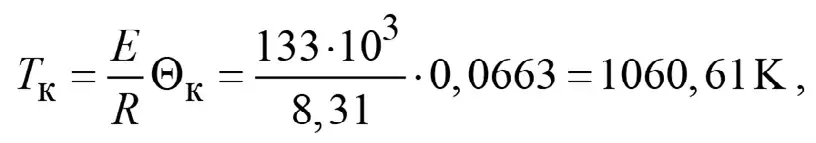
что соответствует температуре по шкале Цельсия, равной 787,61°C.

Далее из (12) получаем формулу для определения периода самовоспламенения:

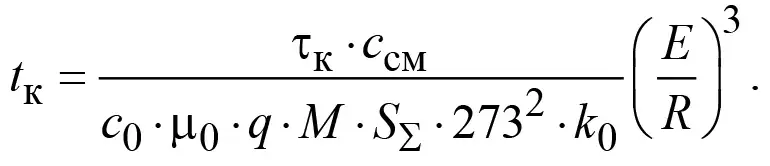(17)

Подставляя в (17) исходные данные и найденные значения τк1 = 4600, τк2 = 5040, τк3 = 3720, вычисляем периоды самовоспламенения:

t_к1 = 41,54 с; t_к2 = 45,51 с; t_к3 = 33,59 с.

Зная период самовоспламенения t_к, можно найти соответствующую длину L_к той части выработки, в которой начинается процесс химического реагирования, заканчивающийся самовоспламенением. Будем полагать, что течение смеси в горной выработке происходит с постоянной скоростью v, в связи с чем имеет место формула: L_к = v·t_к, с помощью которой находим длины L_к1, L_к2, L_к3, соответствующие различным периодам самовоспламенения:

Таким образом, при протекании химического реагирования смеси в адиабатическом режиме период самовоспламенения является наименьшим. И, наоборот, с ростом безразмерного коэффициента теплообмена Ψ период самовоспламенения τк увеличивается. А при достаточно больших значениях Ψ процесс самовоспламенения, вообще может и не произойти, поскольку тепло, образующееся в результате химического реагирования, будет интенсивно поглощаться окружающим массивом. Тем самым критические условия, сопровождаемые скачкообразным ростом температуры, не наступят и самовоспламенения смеси не произойдет.

К сказанному добавим, что существенное влияние на процесс теплообмена с окружающим массивом оказывает температура Θc боковой поверхности выработки. Чем ниже Θ_c, тем интенсивнее происходит теплообмен, в результате которого образующееся тепло уходит в окружающий массив, что с большой долей вероятности исключает процесс самовоспламенения смеси.

Заключение

Основные результаты статьи заключаются в следующем:

– сформулирована задача Коши, описывающая одномерный нестационарный процесс химического реагирования пылегазовоздушной смеси в атмосфере горных выработок;

– ввиду нелинейности задачи Коши ее решение построено численно методом Гира и реализовано с помощью программного пакета Maple V Power Edition;

– полученные значения и построенные графики искомой функции позволили выявить критические условия процесса химического реагирования пылегазовоздушной смеси и найти ее температуру, а также период самовоспламенения;

– на базе выполненного анализа критических состояний процесса химического реагирования пылегазовоздушных смесей с различными параметрами установлено, что наименьшее значение период самовоспламенения смеси имеет место при адиабатическом режиме протекания химического реагирования. С ростом коэффициента теплообмена и с уменьшением температуры боковой поверхности выработки период самовоспламенения увеличивается.

Список литературы

1. Шлапаков П.А., Ерастов А.Ю., Хаймин С.А., Лебедев К.С., Колыхалов В.В., Шлапаков Е.А. Эндогенная пожаробезопасность на угольных предприятиях Кузбасса. Вестник Научного центра ВостНИИ по промышленной и экологической безопасности. 2019;(1):14–21. https://doi.org/10.25558/VOSTNII.2019.69.88.002 Shlapakov P.A., Erastov A.Yu., Khaymin S.A., Lebedev K.S., Kolikhalov V.V., Shlapakov E.A. Endogenous fire safety in kuzbass coal enterprises. Bulletin of Scientific Centre VostNII for Industrial and Environmental Safety. 2019;(1):14–21. (In Russ.) https://doi.org/10.25558/VOSTNII.2019.69.88.002

2. Денисов Е.Т., Саркисов О.М., Лихтенштейн Г.И. Химическая кинетика. М.: Химия; 2000. 568 с. Denisov E.T., Sarkisov O.M., Lichtenstein G.I. Chemical kinetics. Moscow, Khimiya Publ; 2000, 568 p. (In Russ.).

3. Франк-Каменецкий Д.А. Диффузия и теплопередача в химической кинетике. М.: Наука; 1987. 502 с. Frank-Kamenetsky D.A. Diffusion and heat transfer in chemical kinetics. Moscow, Nauka Publ., 1987, 502 p. (In Russ.).

4. Канторович Б.В. Основы теории горения и газификации твердого топлива. М.: Книга по требованию; 2013. 601 с. Kantorovich B.V. Fundamentals of the theory of combustion and gasification of solid fuels. Moscow, Book-on-Demand Publ., 2013, 601 p. (In Russ.).

5. Кремнев О.А., Журавленко В.Я. Тепломассоперенос в горном массиве и подземных сооружениях. Киев: Наукова думка; 1986. 344 с. Kremnev O.A., Zhuravlenko V.Ya. Heat and mass transfer in a rock mass and underground facilities. Kiev, Naukova Dumka Publ., 1986, 344 p. (In Russ.).

6. Виленский Т.В., Хзмалян Д.М. Динамика горения пылевидного топлива. М.: Энергия; 1978. 248 с. Vilensky T.V., Khzmalyan D.M. Dynamics of pulverised fuel combustion. Moscow, Energia Publ., 1978, 248 p. (In Russ.).

7. Кутателадзе С.С. Основы теории теплообмена. М.: Атомиздат; 1979. 416 с. Kutateladze S.S. Fundamentals of the heat transfer theory. Moscow, Atomizdat Publ., 1979, 416 p. (In Russ.).

8. Moiseeva K.M., Krainov A.Yu., Krainov D.A. Two-scale mathematical model of combustion of coal–methane–air gas–particle suspension. Combustion, Explosion, and Shock Waves. 2023;59(1):29–38. https://doi.org/10.1134/S0010508223010033

9. Sidorov A.E., Shevchuk V.G. Laminar flame in fine-particle dusts. Combustion, Explosion, and Shock Waves. 2011;47(518–522. https://doi.org/10.1134/S0010508211050042

10. Sidorov A.E., Shevchuk V.G., Kondrat’ev E.N. Conductive-radiative model of a laminar flame in dust suspensions. Combustion, Explosion, and Shock Waves. 2013;49(257–263. https://doi.org/10.1134/S0010508213030015

11. Vasil’ev A.A. Detonation as combustion in a supersonic flow of a combustible mixture. Combustion, Explosion, and Shock Waves. 2022;58(6):696–708. https://doi.org/10.1134/S0010508222060077

12. Shevchuk V.G., Kondrat’ev E.N., Zolotko A.N., Sidorov A. E., Oparin A.S. Wave regimes of dust combustion. Combustion, Explosion, and Shock Waves. 2014;50(80–86. https://doi.org/10.1134/S0010508214010109

13. Черданцев С.В., Ли Хи Ун, Филатов Ю.М., Шлапаков П.А. Определение критической температуры зажигания микрогетерогенных пылегазовоздушных смесей в горных выработках. Горный информационно-аналитический бюллетень. 2018;(1):117–125. https://doi.org/10.25018/0236-1493-2018-1-0-117-125 Cherdantsev S.V., Lee Khi Un, Filatov Yu.M., Shlapakov P.A. Determination of critical ignition temperature of micro-heterogeneous dust/gas-air mixtures in mines. Mining Informational and Analytical Bulletin. 2018;(1):117–125. (In Russ.) https://doi.org/10.25018/0236-1493-2018-1-0-117-125

14. Черданцев С.В., Шлапаков П.А., Шлапаков Е.А., Лебедев К.С., Ерастов А.Ю. Теплофизические и газодинамические условия протекания процессов дефлаграции и детонации в пылегазовоздушных потоках горных выработок вблизи очагов самонагревания. Химическая физика и мезоскопия. 2019;21(2):179–189. https://doi.org/10.15350/17270529.2019.2.20 Cherdantsev S.V., Shlapakov P.A., Shlapakov Е.A., Lebedev K.S., Erastov A.Yu. Thermophysical and gas-dynamic conditions of deflagration and detonation processes in dust-gas-air flows of mine workings near the centers of self-heating. Chemical Physics and Mesoscopy. 2019;21(2):179–189. (In Russ.) https://doi.org/10.15350/17270529.2019.2.20

15. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Наука; 1974. 331 с. Pontryagin L.S. Ordinary differential equations. Moscow, Nauka Publ., 1974, 331 p. (In Russ.).

16. Самарский А.А., Гулин А.В. Численные методы. М.: Наука; 1989. 432 с. Samarskiy A.A., Gulin A.V. Numerical methods. Moscow, Nauka Publ., 1989, 432 p. (In Russ.).

17. Манзон Б.М. Maple V Power Edition. М.: Филин; 1998. 240 с. Manzon B.M. Maple V Power Edition. Moscow, Filin Publ.; 1998, 240 p. (In Russ.).

18. Постон Т., Стюарт И. Теория катастроф и ее приложения. М.: Физматлит; 1980. 608 с. Poston T., Stewart I. Catastrophe theory and its applications. Moscow, Fizmatlit Publ., 1980, 608 p. (In Russ.).