Повышение оперативности прогноза сейсмической активности при отработке запасов угля на шахтах с применением алгоритмов нейронных сетей

Р.Ю. Замараев, П.В. Гречишкин, О.Л. Гиниятуллина
Кемеровский филиал АО «ВНИМИ», г. Кемерово, Российская Федерация
Горная Промышленность №3S / 2024 стр. 57-62

Резюме: Предложен новый подход к оперативному прогнозу сейсмичности при ведении горных работ на шахтах. В его основе лежит оригинальный взгляд на прогнозирование нестационарных нерегулярных временных рядов с использованием классификатора на основе нейронной сети с архитектурой «SWIN Transformer». Основная решенная задача заключается в разработке схемы преобразования стандартных сейсмологических данных о координатах и магнитудах событий в понятный для нейронной сети образ. Прогноз представляется как вероятность того, что на интервале прогнозирования не появится события с энергией выше установленной границы для класса. Введено три класса событий – с высокой, средней или низкой энергией, границы между которыми определяются статистическими характеристиками магнитуды текущих данных. Интервал прогнозирования задается числом будущих событий. На примере данных одной из шахт оценены свойства распределений координат и магнитуд, оценена точность модели в зависимости от параметров компиляции набора данных, показаны примеры прогнозирования на исторических данных.

Ключевые слова: подземная добыча, сейсмичность, нерегулярные временные ряды, нейронные сети

Для цитирования: Замараев Р.Ю., Гречишкин П.В., Гиниятуллина О.Л. Повышение оперативности прогноза сейсмической активности при отработке запасов угля на шахтах с применением алгоритмов нейронных сетей. Горная промышленность. 2024;(3S):57–62. https://doi.org/10.30686/1609-9192-2024-3S-57-62

Информация о статье

Поступила в редакцию: 03.06.2024

Поступила после рецензирования: 16.07.2024

Принята к публикации: 16.07.2024

Информация об авторах

Замараев Роман Юрьевич – кандидат технических наук, научный сотрудник, Кемеровский филиал АО «ВНИМИ», г. Кемерово, Российская Федерация

Гречишкин Павел Владимирович – кандидат технических наук, директор, Кемеровский филиал АО «ВНИМИ», г. Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Гиниятуллина Ольга Леоновна – кандидат технических наук, старший научный сотрудник, Кемеровский филиал АО «ВНИМИ», г. Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

Нарушение сплошности среды и сложившегося равновесия слоев в ходе добычи полезных ископаемых, как правило, вызывает во вмещающем шахту горном массиве сейсмические явления. Они представляют серьезную опасность для инфраструктуры шахты и жизни горняков, поэтому потребовалась разработка технических, технологических и организационных мероприятий для минимизации риска их возникновения. Значимым элементом организационных мероприятий, очевидно, являются методы прогнозирования сейсмичности, в основе которых можно выделить два подхода.

Первый подход – чисто статистический и исторически – первый. Он состоит в анализе законов распределения свободного потока сейсмических событий в шахтах по энергии, пространству и времени аналогично тектонической сейсмичности. Подобные модели прошли значительный эволюционный путь от первого закона Омори [1] для плотного потока событий в тектонических сейсмоактивных зонах до продвинутых адаптивных решений [2] для зон разреженной сейсмичности и маловероятных событий в шахтах. Модели этого типа используются для определения вероятности возникновения на горизонте прогнозирования от месяца до года сейсмических событий выше определенной магнитуды (обычно) или максимально возможной магнитуды [3].

Второй подход формировался по мере появления работ, доказывающих связь количества и энергии ассоциированных с антропогенным воздействием сейсмических событий в шахтах с объемом извлекаемой горной массы в единицу времени, а также с горно-геологическими условиями и технологиями проведения горных работ, например [4–6].

В рамках этого подхода появились комбинированные модели сейсмической опасности (риска), связывающие параметры наблюдаемой сейсмичности в пространстве и времени с горно-геологическими параметрами типа энергетического индекса (EI), совокупного кажущегося объема (CAV) или частоты сейсмических кажущихся напряжений (ASF) [7–10]. Прогнозные модели этого типа предполагают, что условия добычи существенно не меняются в течение длительных периодов времени. Прогноз составляется для выделенных (активных) областей в окрестности шахты, определяемых кластерами событий и связанных с расположением горных выработок и известными геологическими структурами. Горизонт прогнозирования в этих моделях адаптивный и может меняться от нескольких дней до года.

Сильной стороной первого подхода является универсальность алгоритмов для любого каталога сейсмических событий. С другой стороны, в отношении шахтной сейсмичности нарушается основная гипотеза о свободном потоке событий. Деятельность человека со своей логикой в пространстве и времени становится основным фактором и триггером многих процессов, что негативно влияет на адекватность и точность моделей.

Второй подход позволяет в развитых моделях учесть множество индивидуальных особенностей шахты и в целом всю ситуацию на конкретном объекте, что обеспечивает высокую точность прогноза. Однако об автоматизации учета горно-геологических условий и компоновки шахты говорить не приходится, и каждая модель превращается в артефакт, требующий высочайшей и разносторонней квалификации как разработчика, так и пользователя.

Отдельно следует выделить регрессионный подход к прогнозированию сейсмичности и сейсмического риска. В таких работах обычно используется прием регуляризации времени путем агрегации суммированием энергии событий (целевой показатель) за равные интервалы (день, месяц). В качестве предикторов используются технологические параметры и физико-механические свойства угля, например, как в [11; 12]. В качестве решателей (регрессоров-классификаторов) используются логистическая регрессия, нейронные сети и градиентный бустинг различных модификаций. Основная идея заключается в том, что при определенной цикличности производства и соответствующей повторяемости состояния горного массива формируется связь сейсмичности с одним или несколькими предикторами. В результате удается получить вполне адекватную модель для прогноза на ближайший интервал.

Важно, что в работе [11] целевым показателем выбрана дневная суммарная энергия сейсмических событий, приведенная к бинарному виду относительно заданного уровня. Такой взгляд на регрессию фактически является классификацией, где класс объекта (интервала) определяется сравнением – больше или меньше уровня.

Тем не менее в отношении регрессионного подхода остаются сомнения в корректности неизбирательного суммирования энергий за установленный период, т.к. в него могут попасть события из разных локальных источников и разных потоков, сформированных (вызванных) различными воздействиями и в разное время.

Обобщение качеств статистического и регрессионного подходов позволяет предложить комбинированный подход – использование методов классификаторов с обучением и данных каталогов сейсмических событий (магнитуда и координаты) для прогнозирования того, что в последовательности нескольких будущих событий не окажется события выше установленного уровня. Тогда прогноз как уровень энергии будущего события будет определяться наиболее устойчивой комбинацией показателей предыдущих событий, которые могут быть сколь угодно сложно разделены другими, неинформативными событиями в общем ряду, при этом снимается неопределенность с корректностью и параметрами регуляризации рядов сейсмических событий.

Данные

В качестве источника данных для иллюстраций и примеров использован каталог сейсмических событий за 2022 год одной из шахт Кузбасса, где эксплуатируется система сейсмического мониторинга GITS1. Извлекались значения энергий событий в логарифмическом масштабе ML и координаты X, Y и Z в метрах.

Все манипуляции с данными предполагали, что они станут частью технологии пакетной подготовки данных и обучения модели прогнозирования. Поэтому для очистки данных использованы формальные признаки и кластеризация без обучения, а статистический анализ выполнен на уровне иллюстраций для контроля основных свойств распределений и вычисления требуемых статистических показателей.

Так, за год на прослушиваемой территории системой было зарегистрировано более 10 тыс сейсмических событий магнитудой от 0,6 до 5,1. Первичная очистка данных была выполнена по результатам кластеризации методом k-средних [13], качество кластеризации оценивалось по индексу достоверности (Silhouette score) [14]. В итоге сформировалось ядро данных мощностью 6321 событие, кластеризация которых в пространстве представлена на рис. 1.

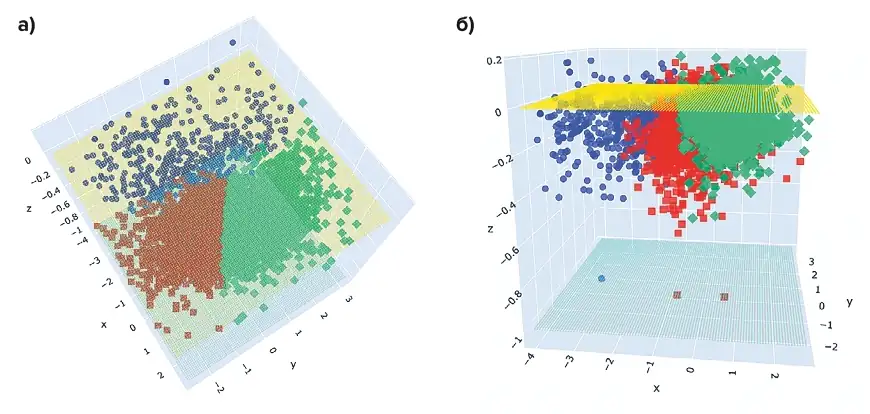Рис. 1 Пространственная композиция сейсмических событий за 2022 г. после очистки данных; координаты X и Y стандартизированные, координаты Z действительные (км)

Fig. 1 Spatial composition of seismic events for 2022 after data cleaning; X and Y coordinates are standardized, Z coordinates are real (km)

Оценка качества кластеризации ядра для числа кластеров составила: 2 – 0,37091; 3 – 0,37645; 4 – 0,33124; 5 – 0,26552; 6 – 0,25770. Из этого следует, что проиллюстрированное на рис. 1 деление событий на 3 кластера обладает наилучшим качеством, но и оно неудовлетворительное. Это подтверждает визуальное восприятие того, что ни в плоскости XY, ни по глубине Z никаких выраженных группировок не проявляется. Подтверждение этому находим в формах распределений показателей на рис. 2.

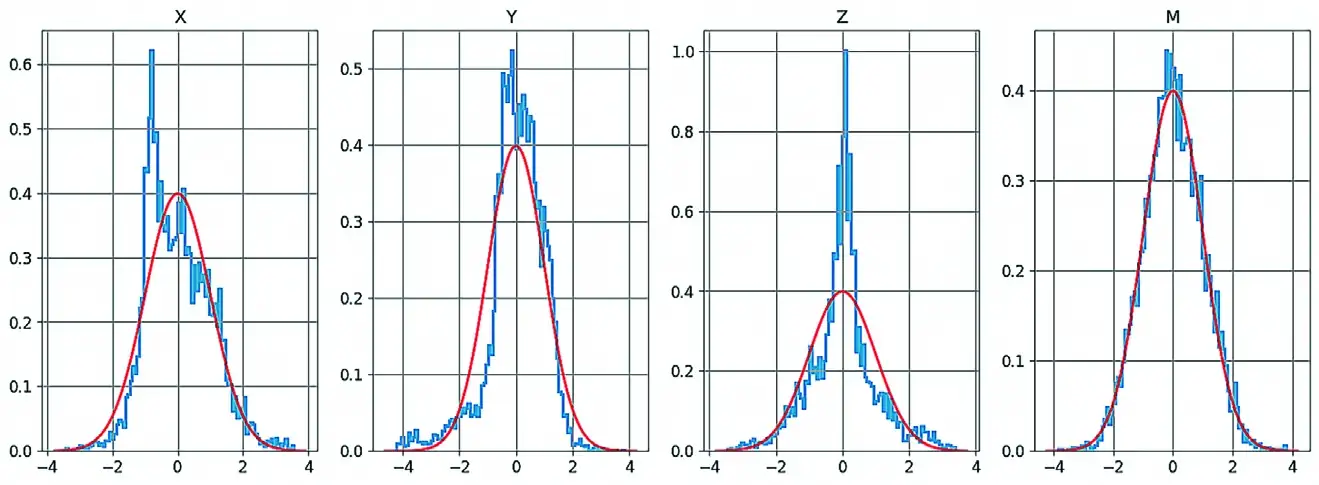Рис. 2 Формы распределений координат и магнитуды сейсмических событий на фоне модели нормального закона распределения; все величины стандартизированные

Fig. 2 Distribution shapes of coordinates and magnitudes of seismic events against the background of the normal distribution law model; all values are standardized

Здесь видно, что распределение координаты Z имеет высокий эксцесс, т.е. выделенные события сильно консолидированы по глубине, полимодальность не просматривается. Координата Y визуально имеет полимодальность, но отдельные пики плотности вероятности приходятся на зону от –2 до 2 среднеквадратического отклонения и статистически их трудно разделить.

Тем не менее неоднородности в распределениях координат X и Y имеются, что свидетельствует о процессе миграции источников выделения сейсмической энергии вслед за перемещениями активных выработок, но с неизвестным отставанием по времени и разбросом по координатам [5].

Почти идеальное соответствие распределения магнитуд нормальному закону приводит к очевидному выводу, что антропогенное воздействие на массив и его отклик сильно зажаты по величине, а отклонения от математического ожидания вызваны большим количеством разнообразных слабых факторов. Среднее значение магнитуды очищенных данных составило 2,150, среднеквадратическое отклонение σ = 0,409 и верхняя граница 3σ отклонения от среднего значения составляет 3,377. Еще одно распределение, свойства и параметры которого характеризуют сейсмичность и важны для последующих решений – это распределение интервалов между событиями. На рис. 3 видно, что этот показатель распределения подобен экспоненциальному. Интервалы менее 1 ч составляют около 80% выборки, а на интервалы менее 5 ч приходится 95%.

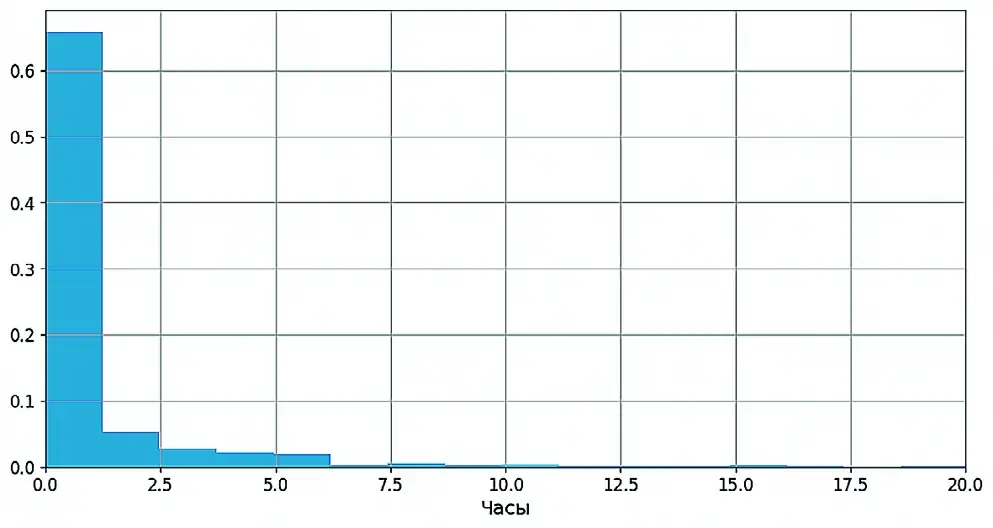Рис. 3 Форма распределения временных интервалов между сейсмическими событиями

Fig. 3 Shape of distribution of time intervals between the seismic events

Методы

Итак, поставлена задача поиска устойчивых комбинаций магнитуды и координат в ряду известных событий (база прогноза), которые на некотором горизонте прогнозирования могут предсказать максимальную магнитуду для некоторого числа будущих событий. При этом полезные для построения образа известные события могут быть случайным образом разделены другими, неинформативными событиями в общем ряду.

Такой сложной постановке соответствуют классификаторы на основе нейронных сетей с архитектурой «трансформеров» [15]. Эта архитектура дает возможность учитывать взаимодействие между атрибутами (словами, значениями), находящимися в данных (текст, ряд, изображение) на произвольно большом расстоянии. Первые варианты трансформеров обладали одним недостатком – размер и положение целевого образа были фиксированными. Адаптация трансформеров под задачи компьютерного зрения [16] привела к архитектуре с подвижным локальным образом. Благодаря этому стало возможным формировать и извлекать из данных целевые образы на разных масштабах и успешно решать задачи сегментации изображений и обнаружения на них объектов.

Имеется несколько свободных библиотек скомпилированных моделей с указанной архитектурой для классификации изображений. Для апробации подхода выбраны базовая библиотека² и конкретная модель «swin-tiny-patch4-window7-224», которая принимает на входе изображение 224×224 пикселей в RGB формате. Чтобы использовать подобные модели, необходимо привести данные каталога событий к приемлемому для них виду. Для этого разработана схема компиляции данных, в которой создается обучающая выборка и подготавливаются данные для прогноза. Ее основные этапы, влияющие на точность прогнозирования, включают:

– выбор числа событий ожидаемого большого N и малого n периодов повторяемости сейсмичности;

– выбор горизонта прогнозирования – числа m будущих событий, для которых прогнозируется предельное значение магнитуды;

– выбор индекса i события, для которого производится классификация-прогноз;

– извлечение базы прогноза – векторов известных значений магнитуды и координат XY с индексами (i – N; i], формирование из векторов трех матриц размером n×(N/n), приведение матриц к нормированному виду (все значения от 0 до 1), агрегация нормированных матриц в RGB изображение, передискретизация (resampling) изображения в требуемый моделью размер;

– если компилируется обучающая выборка, то также извлекаются «будущие» значения магнитуды с индексами (i; i + m], из которых находится максимальное значение , полученное значение сравнивается с границами классов и определяется класс данной базы прогноза;

– границы классов получаются путем деления наблюдаемого диапазона значений магнитуды на статистические или значимые для безопасности уровни.

Важно, что все этапы хорошо автоматизируются, т.е. обучение нескольких вариантов модели для получения приемлемой точности может быть выполнено в одном пакетном задании на подготовленном вычислительном комплексе за несколько часов.

Обучение модели и тестирование

Для подбора параметров и обучения модели из 6321 события было сформировано несколько вариантов обучающей выборки различной мощности. При этом производилось деление магнитуд на три уровня (класса) – низкий, средний и высокий (low, medium, high).

Границы между классами задавались как положительное отклонение от среднего значения магнитуды μ в долях k₁ и k₂ среднеквадратического отклонения σ. Истинный класс каждой базы прогноза определялся по правилу: low if < μ + k₁σ else high if > μ + k₂ σ else medium; k₁ < k₂.

По итогам тестирования установлено, что для использованных данных рациональное число событий малого периода составило 40–50, а большого – 1500–3000. Модели на основе трансформера оказались чувствительны к процедуре передискретизации изображений, поэтому при отсутствии других соображений рационально связать большой и малый периоды как N = n^₂.

Также установлено, что большой горизонт прогнозирования приводит к размыванию образов классов и повышает ложноположительные классификации, а малый горизонт делает модель слишком чувствительной к последним событиям перед прогнозом. Рациональные значения по итогам тестирования составили 5–10 событий. Коэффициенты k₁ и k₂ были определены с точностью до 0,1 как 1,4 и 2,6, что дало в действительных значениях магнитуды 2,680 и 3,127 соответственно. С этими значениями определились истинные значения классов и проводилось обучение моделей с последующим тестированием, оценкой средней точности и построением матриц ошибок.

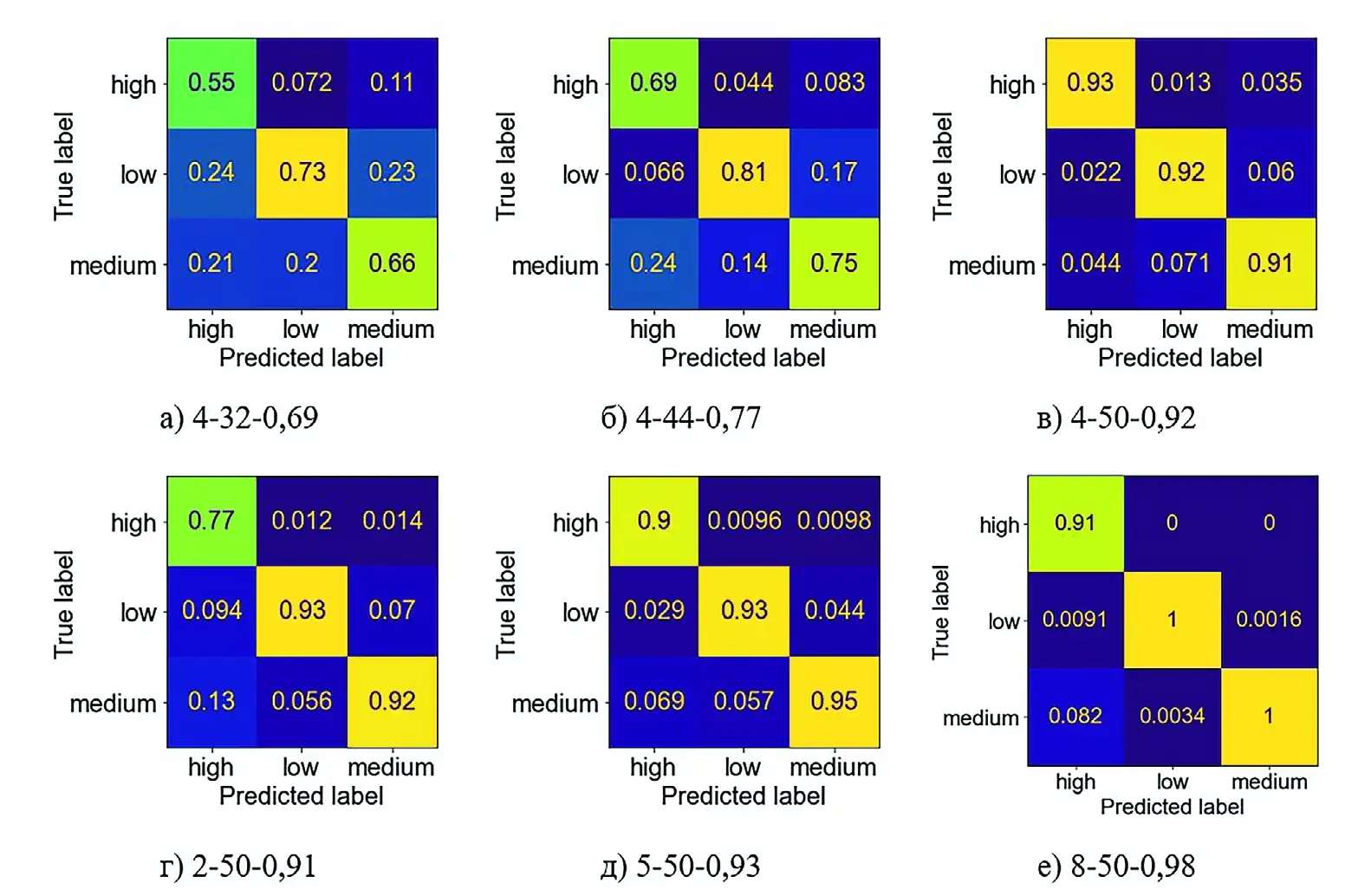Рис. 4 Сравнение качества моделей

Fig. 4 Comparison of the model quality

На рис. 4 приведены некоторые результаты тестирования моделей в виде матриц ошибок. Под каждой матрицей указаны горизонт прогнозирования, малый период прогнозирования и средняя точность соответственно. Можно видеть, что приемлемая средняя точность свыше 90% достигается при 50 событиях в малом периоде, что дает 2500 событий в большом периоде (рис. 4, в–е). Малый горизонт прогнозирования при приемлемой средней точности дает неприемлемую точность определения высокоэнергетических событий – почти 9% вероятности для слабого события и 13% для среднего события ложноположительной классификации как сильного.

Очевидно, что прогноз появления именно сильного события представляет наибольший интерес. Поэтому в итоге лучшей признана модель с параметрами на рис. 4, е, у которой средняя точность 98% и менее 1% вероятности для слабого события и 8% для среднего события ложноположительной классификации как сильного. На рис. 5 показана классификация-прогноз на исторических данных. Ряд значений магнитуды представлен простой последовательностью без привязки ко времени.

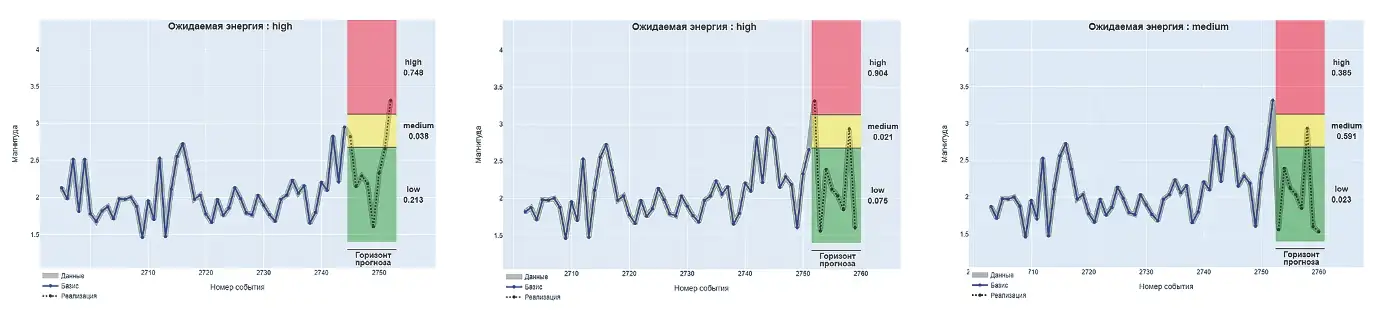Рис. 5 Пример классификации-прогноза для одного события

Fig. 5. xample of classification-forecasting for a single event

Базис представлен последним малым периодом (50 значений). Горизонт прогнозирования (8 значений) представлен последующей известной реализацией. На рис. 5, а показано, что на ближайшие 8 событий прогнозируется появление как минимум одного высокоэнергетического (ML > 3,127) и, как видно, оно присутствует. Пока его признаки сохраняются по мере появления новых событий, сохраняется и прогноз (рис. 5, б), но меняется достоверность заключения в зависимости от силы признаков от 0,748 до 0,904. Как только прогнозируемое высокоэнергетическое событие происходит (рис. 5, в) и признаки такового пропадают, происходит смена прогнозируемого класса на средний.

Эволюция прогноза на множестве событий со сменой класса показана на рис. 6. Вертикальные черные линии показывают место смены класса, в пределах каждого класса сверху указана средняя достоверность заключения.

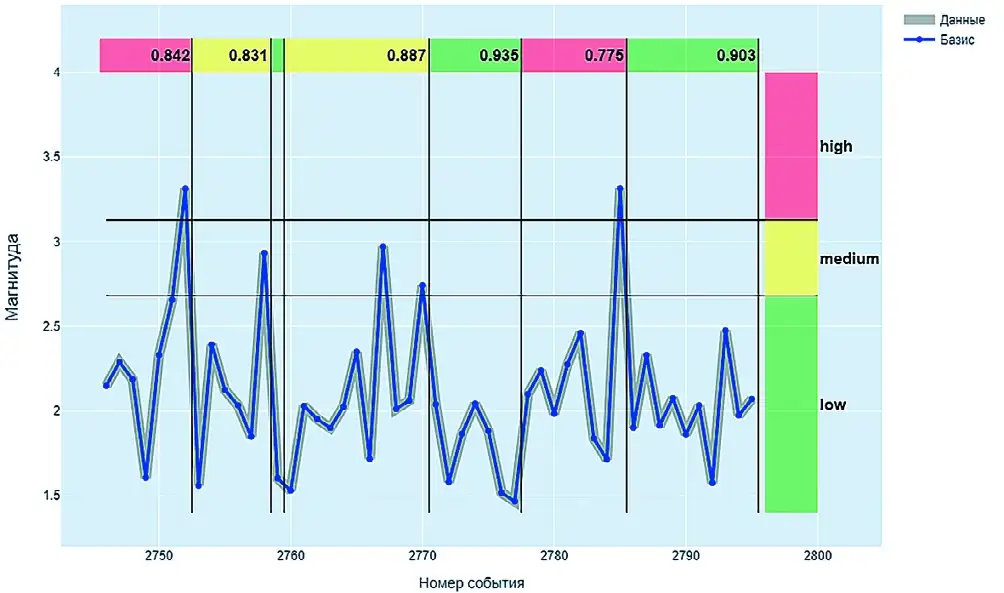Рис. 6 Пример классификации- прогноза для множества событий

Fig. 6 Example of classificationforecasting for multiple events

Особое место занимает вопрос проекции прогноза на реальное время. Здесь может быть выбрано статистическое решение: для известного числа интервалов прогнозирования, которое равно горизонту m, и размеров интервалов Δt таких, что P(Δt ≤ t_max ) ≤ P_max, можно оценить реальное время T, эквивалентное горизонту прогнозирования как T ≤ mt_max ‰ p = . Например, для использованных данных и параметров модели при P_max = 0,95 получим, что t_max = 5 ч и прогноз актуален не более 40 ч с вероятностью 66%.

Выводы

Предложен новый подход к оперативному прогнозу сейсмичности при ведении горных работ на шахтах. В его основе лежит оригинальный взгляд на прогнозирование нестационарных нерегулярных временных рядов с использованием классификатора на основе нейронной сети с архитектурой «SWIN Transformer». Прогноз представляется как вероятность того, что на интервале прогнозирования не появится события с энергией выше установленной границы. На примере данных одной из шахт оценены свойства распределений координат и магнитуд, оценена точность модели в зависимости от параметров компиляции набора данных, показаны примеры прогнозирования на исторических данных. Подготовка модели, обучение и прогноз в условиях конкретной шахты хорошо автоматизируются, для чего используются данные только каталогов сейсмических событий.

Список литературы

1. Utsu T., Ogata Y., Matsu’ura R.S. The centenary of the Omori formula for a decay law of aftershock activity. Journal of Physics of the Earth. 1995;43(1):1–33. https://doi.org/10.4294/jpe1952.43.1

2. Helmstetter A., Werner M.J. Adaptive smoothing of seismicity in time, space, and magnitude for time‐dependent earthquake forecasts for California. Bulletin of the Seismological Society of America. 2014;104(2):809–822. https://doi.org/10.1785/0120130105

3. Kijko A., Funk C.W. The assessment of seismic hazards in mines. The Journal of The South African Institute of Mining and Metallurgy. 1994;94:179–185.

4. Маловичко А.А., Завьялов А.Д., Козырев А.А. Горные удары. В кн.: Соболев Г.А. (ред.) Природные опасности России. Т. 1. Сейсмические опасности. М.: Крук; 2000. С. 243–293.

5. Мельников Н.Н. (ред.). Сейсмичность при горных работах. Апатиты: Кольский научный центр РАН; 2002. 325 с.

6. Мустафин М.Г. Механизм возникновения горных ударов с разрушением почвы выработок. Записки Горного института. 2016;217:40–48. Режим доступа: https://pmi.spmi.ru/pmi/article/view/5080 (дата обращения: 15.05.2024). Mustafin M.G. The mechanism of rock burst leading to ground destruction of mine openings. Journal of Mining Institute. 2016;217:40–48. (In Russ.) Available at: https://pmi.spmi.ru/pmi/article/view/5080 (accessed: 15.05.2024).

7. van Aswegen G. Routine seismic hazard assessment in mines. In: Potvin Y., Hudyma M. (eds). RaSiM6: Proceedings of the Sixth International Symposium on Rockburst and Seismicity in Mines Proceedings. Perth: Australian Centre for Geomechanics; 2005, pp. 437–444. https://doi.org/10.36487/ACG_repo/574_45

8. Mendecki A.J. Forecasting seismic hazard in mines. In: Potvin Y., Carter J., Dyskin A., Jeffrey R. (eds) SHIRMS 2008: Proceedings of the First Southern Hemisphere International Rock Mechanics Symposium. Perth: Australian Centre for Geomechanics; 2008, pp. 55–69. https://doi.org/10.36487/ACG_repo/808_101

9. Nordström E., Dineva S., Nordlund E. Back analysis of short-term seismic hazard indicators of larger seismic events in deep underground mines (LKAB, Kiirunavaara Mine, Sweden). Pure and Applied Geophysics. 2020;177(2):763–785. https://doi.org/10.1007/s00024-019-02352-8

10. Разумов Е.Е., Рукавишников Г.Д., Мулёв С.Н., Простов С.М. Анализ сейсмической активности массива при ведении горных работ на шахте «Комсомольская» АО «Воркутауголь». Горный информационно-аналитический бюллетень. 2022;(1):104–114. https://doi.org/10.25018/0236_1493_2022_1_0_104 Razumov E.E., Rukavishnikov G.D., Mulev S.N., Prostov S.M. Seismic activity in rock mass during mining operations in Vorkutaugol’s Komsomolskaya mine. Mining Informational and Analytical Bulletin. 2022;(1):104–114. (In Russ.) https://doi.org/10.25018/0236_1493_2022_1_0_104

11. Jakubowski J., Tajdus A. Predictive regression models of monthly seismic energy emissions induced by longwall mining. Archives of Mining Sciences. 2014;59(3):705–720. https://doi.org/10.2478/amsc-2014-0049

12. Jakubowski J. A predictive model of daily seismic activity induced by mining, developed with data mining methods. Geoinformatica Polonica. 2014;13(1):7–19. https://doi.org/10.2478/gein-2014-0001

13. MacQueen J. Some methods for classification and analysis of multivariate observations. In: Le Cam L.M., Neyman J. (eds) Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics. Berkeley, Calif.: University of California Press; 1967, pp. 281–297. Available at:https://sci2s.ugr.es/keel/pdf/algorithm/congreso/1967-MacQueen-MSP.pdf (accessed: 15.05.2024).

14. Rousseeuw P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. Journal of Computational and Applied Mathematics. 1987;20:53–65. https://doi.org/10.1016/0377-0427(87)90125-7

15. Vaswani A., Shazeer N., Parmar N., Uszkoreit J., Jones L., Gomez A.N. et al. Attention is all you need. In: 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA; 2017, pp. 1–11.

16. Liu Z., Lin Y., Cao Y., Hu H., Wei Y., Zhang Z. et al. Swin transformer: Hierarchical vision transformer using shifted windows. In: 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. IEEE; 2021, pp. 9992–10002. https://doi.org/10.1109/ICCV48922.2021.00986