Вариационный метод оценки устойчивости откосов

А.В. Жабко^{1, 2
1} Уральский филиал АО «ВНИМИ», г. Екатеринбург, Российская Федерация
² Уральский государственный горный университет, г. Екатеринбург, Российская Федерация
Горная Промышленность №3S / 2024 стр. 06-13

Резюме: В статье рассматривается вариационный метод (способ) оценки устойчивости откосов, который основан на методе предельного равновесия, но в отличие от инженерных способов оценки устойчивости позволяет математически (вариационное исчисление) обосновать единственную наиболее опасную поверхность скольжения в массиве, включая углы ее изломов и распределение межблоковых реакций на ее различных участках. Основными идеями и положениями предлагаемой теории или концепции – вариационного метода расчета устойчивости откосов являются: 1) определение формы и положения в массиве поверхности скольжения должно обосновываться строгими математическими (вариационными) методами, а не подбором поверхности скольжения заданной формы, например, круглоцилиндрической; 2) расчет или оценка устойчивости, а более конкретно, подсчет сдвигающих и удерживающих сил на различных участках поверхности скольжения в зависимости от геометрии поверхности скольжения и откоса, а также механических характеристик пород и контактов осуществляется с использованием различных функционалов (обобщенной силы). В статье автор показывает, что при применении инженерных способов расчета устойчивости откосов для различных форм их потери устойчивости, в отличие от вариационного метода, резко завышаются их предельные (проектные) параметры. Это, на взгляд автора, является первопричиной многих аварий, связанных с разрушением откосных сооружений. Применение вариационного метода оценки устойчивости откосов позволило установить новые формы потери устойчивости откосов и объяснить наблюдаемые на практике аномально крутые углы наклона сдвиговых площадок.

Ключевые слова: откос, расчет устойчивости, предельные параметры откосов, поверхность скольжения, поверхность ослабления, угол внутреннего трения, подошвенный оползень, подподошвенный оползень

Для цитирования: Жабко А.В. Вариационный метод оценки устойчивости откосов. Горная промышленность. 2024;(3S):06–13. https://doi.org/10.30686/1609-9192-2024-3S-06-13

Информация о статье

Поступила в редакцию: 10.05.2024

Поступила после рецензирования: 18.06.2024

Принята к публикации: 25.06.2024

Информация об авторе

Жабко Андрей Викторович – доктор технических наук, доцент, заведующий лабораторией устойчивости бортов карьеров, Уральский филиал АО «ВНИМИ»; заведующий кафедрой маркшейдерского дела, Уральский государственный горный университет, г. Екатеринбург, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

Вопросы устойчивости бортов карьеров, откосов отвалов, дамб различного назначения, котлованов и т.д. являются достаточно актуальными, что следует из непрерывно пополняющихся научных исследований по данному вопросу, как отечественных [1–9], так и зарубежных [10– 15], появляющихся новых нормативных документов1 и т.д. Суть расчета устойчивости откосов и определения их предельных параметров по методу предельного равновесия сводится к определению положения поверхности скольжения в массиве и оценке вдоль нее удерживающих и сдвигающих обобщенных сил (силы, моменты сил).

На сегодняшний день большинство расчетов выполняются с использованием программного обеспечения, например, Slide, Geo-slope, Geo-studio и др., которые реализуют ряд так называемых инженерных способов оценки устойчивости (Fellenius, Bishop, Spenser, Teylor, Morgenstern-Price, Janbu и мн. др.). Какой из данных способов является более точным в конкретных условиях, сказать не представляется возможным, какие погрешности дает каждый из этих способов, оценить также невозможно в силу того, что каждый из этих способов наделен определенными недостатками, из-за которых их и относят к оценочным или приближенным. Основные недостатки, характерные для инженерных способов оценки устойчивости, следующие:

1. Необоснованность междублоковых реакций смежных блоков или отсеков. Это приводит к тому, что каждый из инженерных способов расчета прогнозирует свое значение коэффициента устойчивости и параметры наиболее слабых поверхностей скольжения (призм смещения).

Касательная составляющая междублоковой реакции необоснованно принимается от нуля до максимально возможного кулоновского значения, что является следствием статической неопределимости задачи по установлению условий равновесия отсека.

2. Необоснованность формы поверхности скольжения (для расчета откосов используются, как правило, простейшие формы поверхностей скольжения – дуга окружности, логарифмическая спираль и т.д., которые не имеют должного теоретического обоснования), включая излом поверхности скольжения при переходе в литологический слой с иными механическими характеристиками (неоднородный откос, неустойчивое или слабое основание сооружения), излом поверхности скольжения при встрече со слабым контактом (контакты литологических разностей, прочные породы или прислоненный откос, трещины большого протяжения и тектонические нарушения, другие поверхности ослабления массива) – анизотропный откос, контактный оползень.

3. Инженерные способы расчета, в том числе все существующие современные компьютерные отечественные и зарубежные программы, реализующие данные способы, не позволяют учитывать изменение закона распределения междублоковой реакции вдоль поверхности скольжения. Дело в том, что на различных участках поверхности скольжения, в том числе участках, определяемых анизотропией массива, междублоковая реакция распределяется по-разному, что приводит к тому, что на каждом участке необходимо использовать свой функционал (формулу) для оценки сдвигающих и удерживающих сил. Например, на участках под откосом, где поверхность скольжения формируется в массиве вследствие дилатансионных процессов (увеличение объема в пластической фазе деформирования), будет возникать повышенная межблоковая реакция, а на участках, где поверхность скольжения предопределена геологическим строением (слабый контакт), междублоковой реакции возникать не будет и разрушение будет происходить в виде смещения «жесткого клина». Другими словами, программные продукты по оценке устойчивости откосов и оснований могут учесть геометрию контактов и самой поверхности скольжения (ручной режим задания поверхности скольжения), но не могут физику (механику) процесса разрушения посредством использования нужного функционала. Именно поэтому область применения современных программных продуктов по оценке устойчивости откосов (Slide, Geo-slope, Geo-studio и др.) ограничивается изотропными откосами на устойчивом основании.

Погрешность оценки устойчивости обычно определяется по внутренней сходимости между данными различными способами оценки устойчивости или способами подсчета сил, сдвигающих и удерживающих призму смещения. Однако имеется целый ряд доказательств того, что погрешности расчета устойчивости и определения предельных параметров откосов значительно выше, приведем два резонансных примера.

В Бразилии на руднике Córrego do Feijão Mine в январе 2019 г. была разрушена дамба хвостохранилища. В результате данной техногенной катастрофы погибло около 300 человек, под селевыми массами объемом примерно 12 млн м³ погребено 130 вагонов, разрушен мост, ядовитыми отходами обогащения загрязнено примерно 300 км рек. Второй случай произошел 1 апреля 2015 г. в результате мощного оползня объемом 27,5 млн м³ внешнего отвала разреза «Заречный» в Кузбассе. Оползнем повреждена ЛЭП, часть железнодорожных путей и подвижной состав, автомобили и склад ГСМ, завалены русла рек.

Отметим, что оползень отвала разреза «Заречный» произошел при его высоте, немногим превышающей 120 м, при проектной более чем 200 м, а рассматриваемая дамба хвостохранилища накануне аварии, согласно отчету авторитетной немецкой специализированной мониторинговой организации TÜV SÜD, по большинству поперечных разрезов на всю свою высоту имела запас близкий к двум, однако и в первом, и во втором случаях разрушение сооружений произошло. Весьма показательно, что расчет устойчивости бразильской дамбы хвостохранилища был выполнен с помощью программы Slide 7.0, разработанной компанией Rocscience, расчетный способ – Spenser, по круглоцилиндрической поверхности скольжения, вместе с тем после произошедшего оползания было видно, что поверхность скольжения абсолютно не похожа на дугу окружности, особенно в своей верхней части с весьма крутым наклоном сдвиговых площадок (имеются фотои видеоматериалы). Показательность данных примеров для дальнейших рассуждений заключается в том, что в обоих случаях практически исключается влияние на погрешность прогноза устойчивых параметров других факторов, кроме погрешности самого расчета. То есть ни погрешности в определении механических характеристик, ни резкого обводнения, ни сейсмического воздействия либо не было, либо они не могли привести к столь большим погрешностям расчета.

Сравнение предельных параметров, полученных инженерными и вариационным методами

В данной работе речь пойдет о вариационном способе (методе) оценки устойчивости и определения предельных параметров откоса. Сразу оговоримся, что использование вариационного метода оценки устойчивости откосов (при тех же характеристиках пород и тех же условиях обводнения и др.) позволило установить, что предельные параметры Бразильской дамбы и отвала «Заречный» полностью соответствуют фактическим параметрам на момент их разрушения (данные будут опубликованы в отдельной статье). Поэтому главной причиной данных трагических событий является некорректный расчет их устойчивости, включая расчетную схему, определение наиболее вероятной поверхности скольжения и способ расчета сдвигающих и удерживающих сил вдоль данной поверхности.

Вариационный способ оценки устойчивости, получивший свое развитие главным образом в трудах таких ученых, как Н.М. Герсеванов, J. Kopacsy, А.Г. Дорфман, М.Н. Гольдштейн, С.Г. Кушнер, М.И. Шевченко [16], Ю.И. Соловьев [17], применительно к задачам обеспечения устойчивости горнотехнических сооружений – А.В. Жабко [18; 19] и рекомендуемый к использованию Федеральными нормами и правилами в области промышленной безопасности2, не имеет указанных выше недостатков и позволяет получить более точные результаты, при этом в силу того, что наиболее слабая (опасная) поверхность скольжения обосновывается математически (вариационное исчисление), включая углы ее излома, прогнозируемые коэффициенты устойчивости всегда меньше коэффициентов устойчивости, полученных инженерными способами.

Вариационный способ расчета устойчивости откосов или определения их предельных параметров относится к аналитическому способу. Принципиальное отличие данного способа заключается в том, что инженерные способы подразумевают задание множества поверхностей скольжения, как правило, простейшего типа (плоская, круглоцилиндрическая, логарифмическая спираль и т.д.) и отыскание среди них перебором наиболее опасной, то есть имеющей минимальный коэффициент устойчивости. При использовании такого перебора однотипных поверхностей скольжения не представляется возможным выявить механизм нарушения устойчивости откоса.

Напротив, вариационный способ позволяет с помощью вариационного исчисления (математического анализа) напрямую определить форму и положение наиболее слабой поверхности скольжения в откосе, а также определить предельные параметры откосов и призмы смещения. В этой связи для решения задач вариационным способом необходимо аналитически или численно решить систему уравнений предельного равновесия при условии экстремума обобщенной силы.

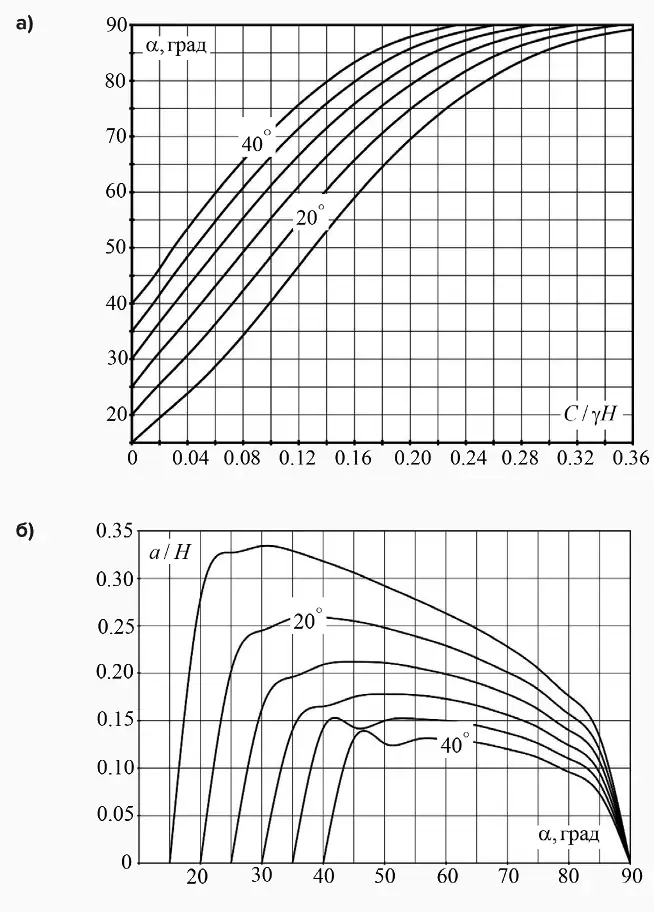Рис. 1 Номограмма для определения предельных параметров однородного откоса (а) и номограмма для определения ширины призмы обрушения в однородном откосе (б)

Fig. 1 A nomographic chart for defining the limiting parameters of a homogeneous slope (а), and a nomographic chart for defining the width of the sliding wedge in a homogeneous slope (б)

В результате численного решения уравнений, определяющих наиболее опасную поверхность скольжения, определены предельные параметры плоских однородных откосов и построена номограмма устойчивости (рис. 1, а), а также номограмма для определения ширины призмы обрушения однородных откосов (рис. 1, б).

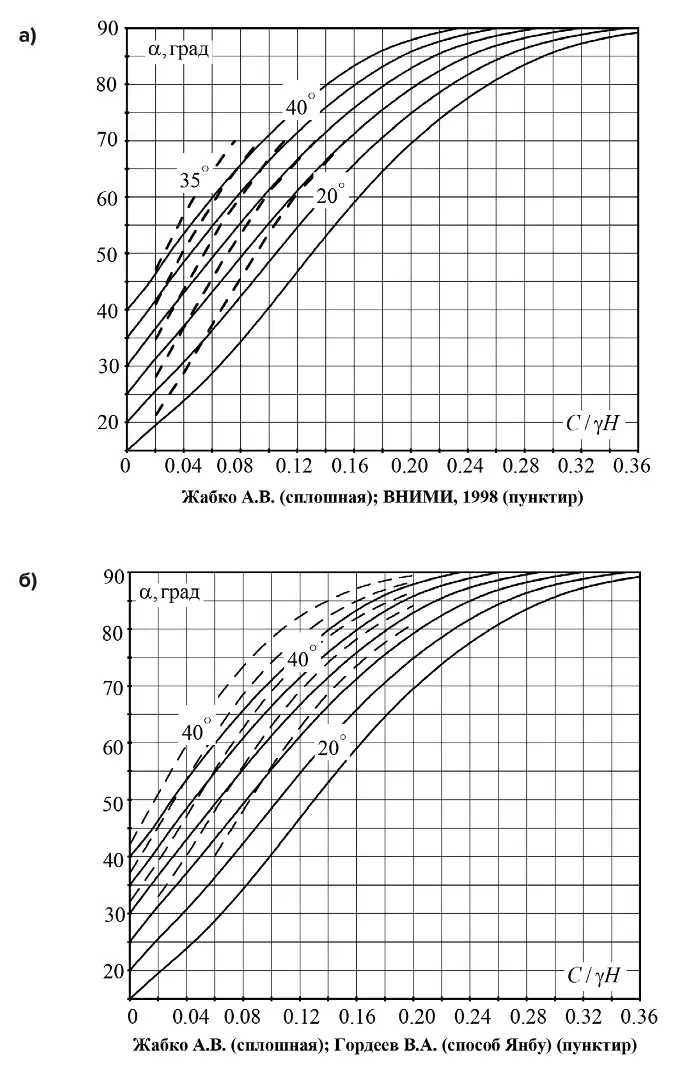Рис. 2 Сравнение предлагаемых графиков устойчивости Жабко А.В. (сплошная) с данными ВНИМИ, 1998 (пунктир) (а) и СНИП 45.13330.2012 (пунктир) (б)

Fig. 2 Comparison of the proposed stability graphs by A.V. Zhabko (solid line) with the VNIMI data, 1998 (dashed line) (а) and SNIP 45.13330.2012 (dotted line) (б)

На рис. 2, а приведено сравнение полученных графиков устойчивых откосов с графиками, рекомендуемыми Правилами обеспечения устойчивости откосов на угольных разрезах3 (далее – Правила обеспечения устойчивости). Анализ данных графиков показывает, что рекомендуемый нормативным документом предельный угол устойчивых откосов завышен относительно предлагаемого автором на и более градусов. Меньшие значения расхождений соответствуют высоким откосам (бортам карьера) и составляют 2-5 градусов, что является достаточно существенным.

Для высоких откосов рекомендации СНиП (рис. 2, б) также прогнозируют завышенные значения углов откосов на 2 и более градусов, в зависимости от угла внутреннего трения и высоты откоса. Для невысоких откосов разница становится весьма существенной. Завышения углов устойчивых откосов прогнозируют и расчеты способами Janbu (Янбу) и D. Taylor (Тейлора) (рис. 3, а, б), однако для высоких откосов разница с автором уже менее значительна, а для небольших по высоте откосов разница углов откоса также возрастает.

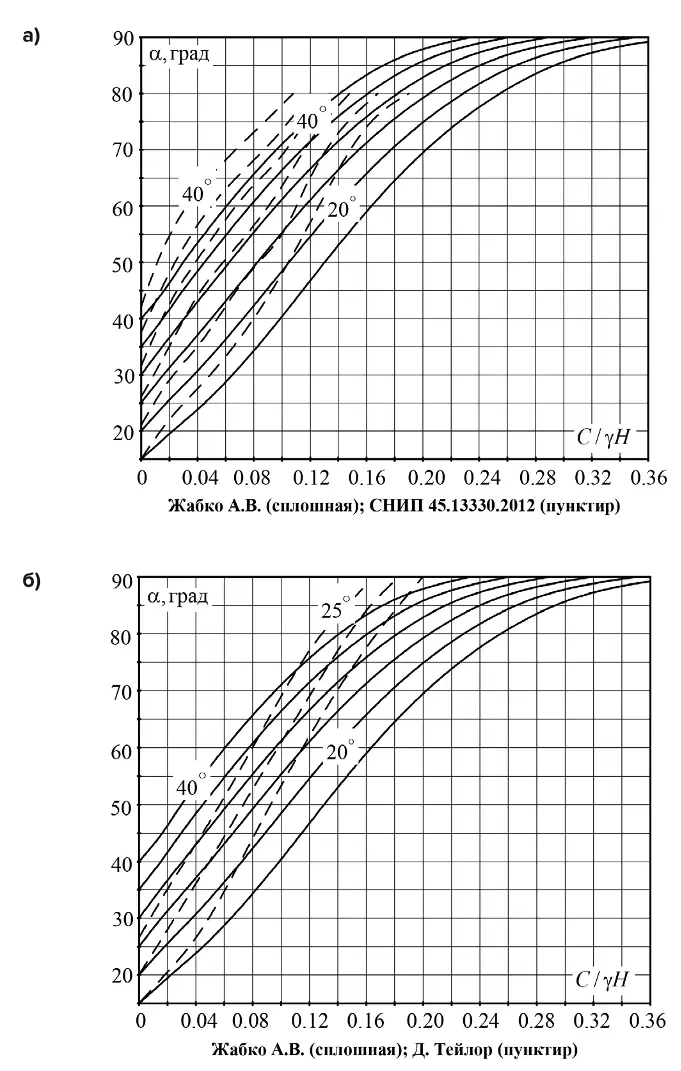Рис. 3 Сравнение предлагаемых графиков устойчивости А.В. Жабко (сплошная) с данными В.А. Гордеева (способ Янбу, пунктир) (а) и Д. Тейлора (пунктир) (б)

Fig. 3 Comparison of the proposed stability graphs by A.V. Zhabko (solid line) with the data by V.A. Gordeev (the Janbu’s method, dotted line) (а) and D. Taylor (dashed line) (б)

Прогнозирование завышенных значений углов откосов всеми рассмотренными способами и нормативными документами относительно предлагаемых объясняется недостаточной обоснованностью формы и положения, используемых в расчетах потенциальных поверхностей скольжения. Кроме того, значительные различия углов откоса (см. рис. 2, а) объясняются использованием расчетных схем с переоцененным вкладом в устойчивость касательной межблоковой реакции.

Необходимо отметить, что только предлагаемая теория (вариационный метод) прогнозирует для сыпучих пород (С = 0) плоскую поверхность скольжения, совпадающую с откосом, и его устойчивый угол, равный углу внутреннего трения (углу естественного откоса). Все известные в мире способы (инженерные), схемы расчета и т. д. не удовлетворяют данному теоретическому условию по уже упомянутой причине – недостаточная обоснованность геометрии поверхности скольжения.

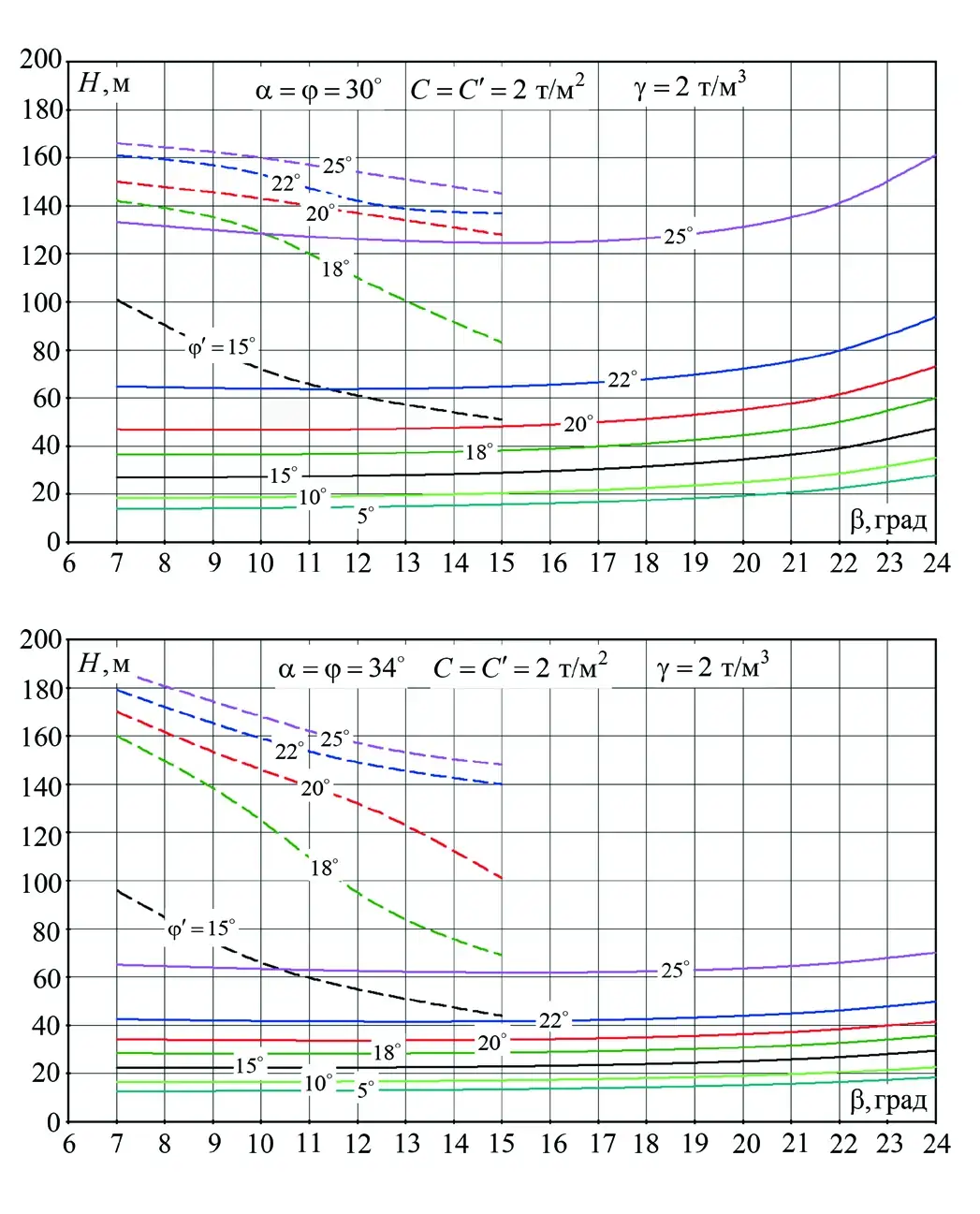Рис. 4 Номограммы устойчивости отвалов при контактной схеме разрушения

Fig. 4 Nomographic charts of dump stability under the contact failure scheme

Теперь проведем сравнение номограмм устойчивости откосов отвалов, полученных вариационным методом и рекомендованных Правилами обеспечения устойчивости для контактной схемы нарушения устойчивости. Сплошными линиями на рис. 4 приводятся графики, полученные вариационным методом, а пунктиром – рекомендуемые Правилами обеспечения устойчивости. Как следует из результатов расчета, для контактной схемы нарушения устойчивости инженерные методы весьма значительно завышают предельную высоту (угол откоса) отвала.

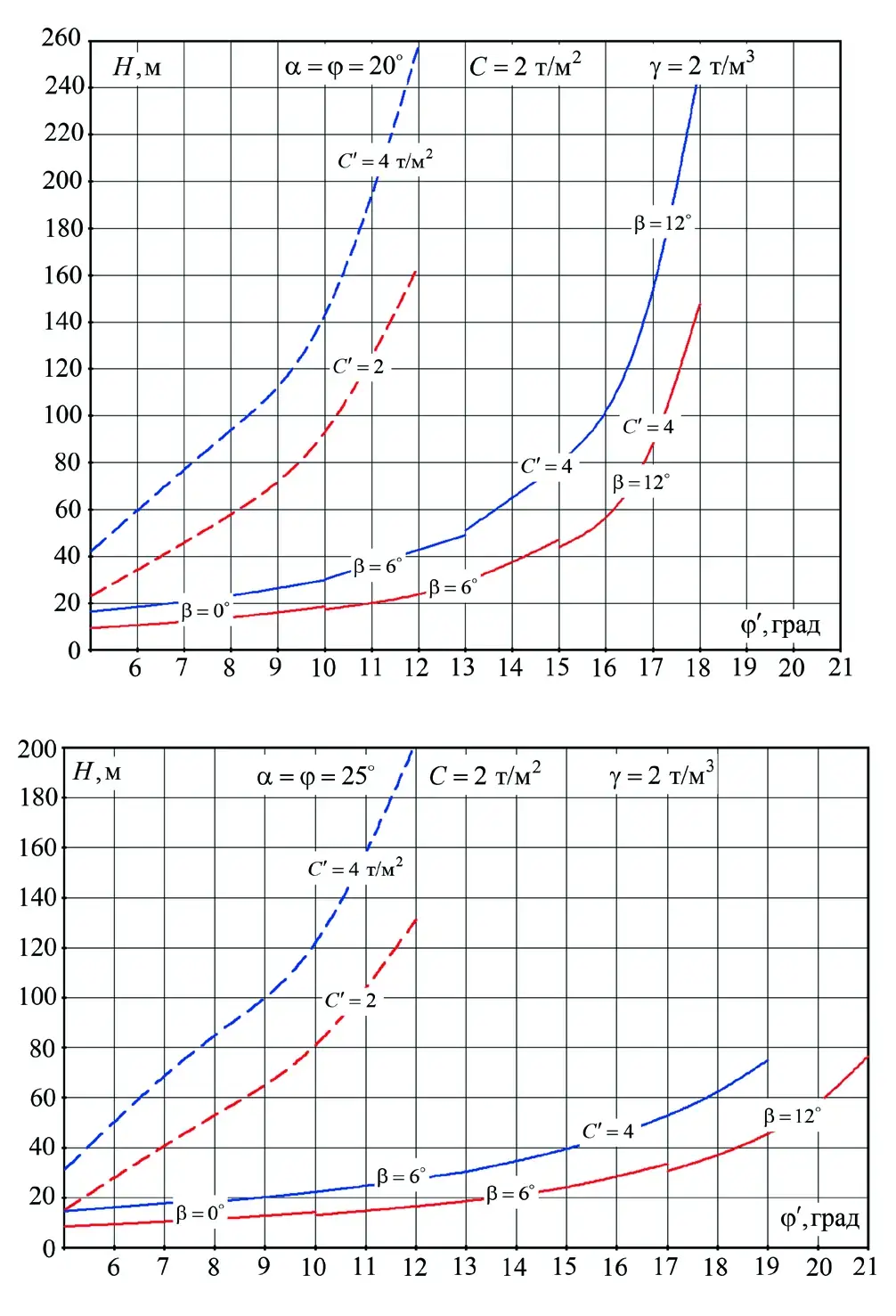Рис. 5 Номограмма устойчивости отвалов на слабом основании

Fig. 5 A nomographic chart of dump stability on weak base

На рис. 5 приведена номограмма для определения предельных параметров отвалов на слабом основании (сплошная – А.В. Жабко [19], пунктир – Правила обеспечения устойчивости). Как видно, и в этом случае погрешности прогноза предельных параметров откосов, полученные инженерными методами, достаточно велики. Кроме того, как видно из графиков, полученных вариационным методом расчета, поверхность скольжения в зависимости от угла наклона основания может выходить в основание откоса и при достаточно больших значениях его угла внутреннего трения (до 21 град). Таким образом, вариационный метод расчета устойчивости позволяет выявить и расширить понятие слабого основания, то есть учесть вклад угла наклона основания в его устойчивость.

Основы расчета устойчивости вариационным методом

Как уже отмечалось выше, инженерные методы расчета устойчивости откосов прогнозируют завышенные устойчивые параметры откосных сооружений (борта, отвалы, дамбы и т.д.). Однако, кроме этого, они не позволяют оценить реальную схему потери устойчивости откосов, параметры призмы смещения (ширину) и т.д. Это связано с тем, что поверхности скольжения в программах задаются, как правило, простейших форм и без каких-либо граничных условий, отвечающих существующим теоретическим положениям законов разрушения горных пород. Далее с помощью компьютерной программы или ручным счетом просто отбирается поверхность скольжения с наибольшей разницей между сдвигающей и удерживающей обобщенной силой и считается, что расчет закончен. Разумеется, такой расчет никогда не выявит реальную форму поверхности скольжения, а соответственно, и параметры призмы смещения.

Принципиальным положением предлагаемой концепции (вариационного метода): на различных участках поверхности скольжения, в зависимости от углов ее наклона и угла наклона откоса на рассматриваемом участке, а также наличия поверхностей ослабления, частично или полностью совпадающих с поверхностью скольжения, для подсчета сдвигающих и удерживающих сил должен применяться конкретный функционал (формула), что связано с различием в распределении межблоковой реакции (реакции между смежными отсеками). Еще одним принципиальным отличием является то, что согласно существующим представлениям, заложенным в инженерные методы расчета, поверхность скольжения не может превышать угол наклона равный , что, конечно же, не соответствует действительности, достаточно взглянуть на верхнюю часть поверхности скольжения любого оползня, в частности, оползня бразильской дамбы. В табл. 1 приведены формулы (подынтегральные выражения или обобщенная сила) для подсчета сдвигающих и удерживающих сил вдоль поверхности скольжения, на различных ее участках согласно разработанной концепции.

Таблица 1 Функционалы (формулы) расчета сил вдоль поверхности скольжения и условия их применения

Table 1 Composite functions (formulas) to calcilate forces along the slip surface and conditions of their application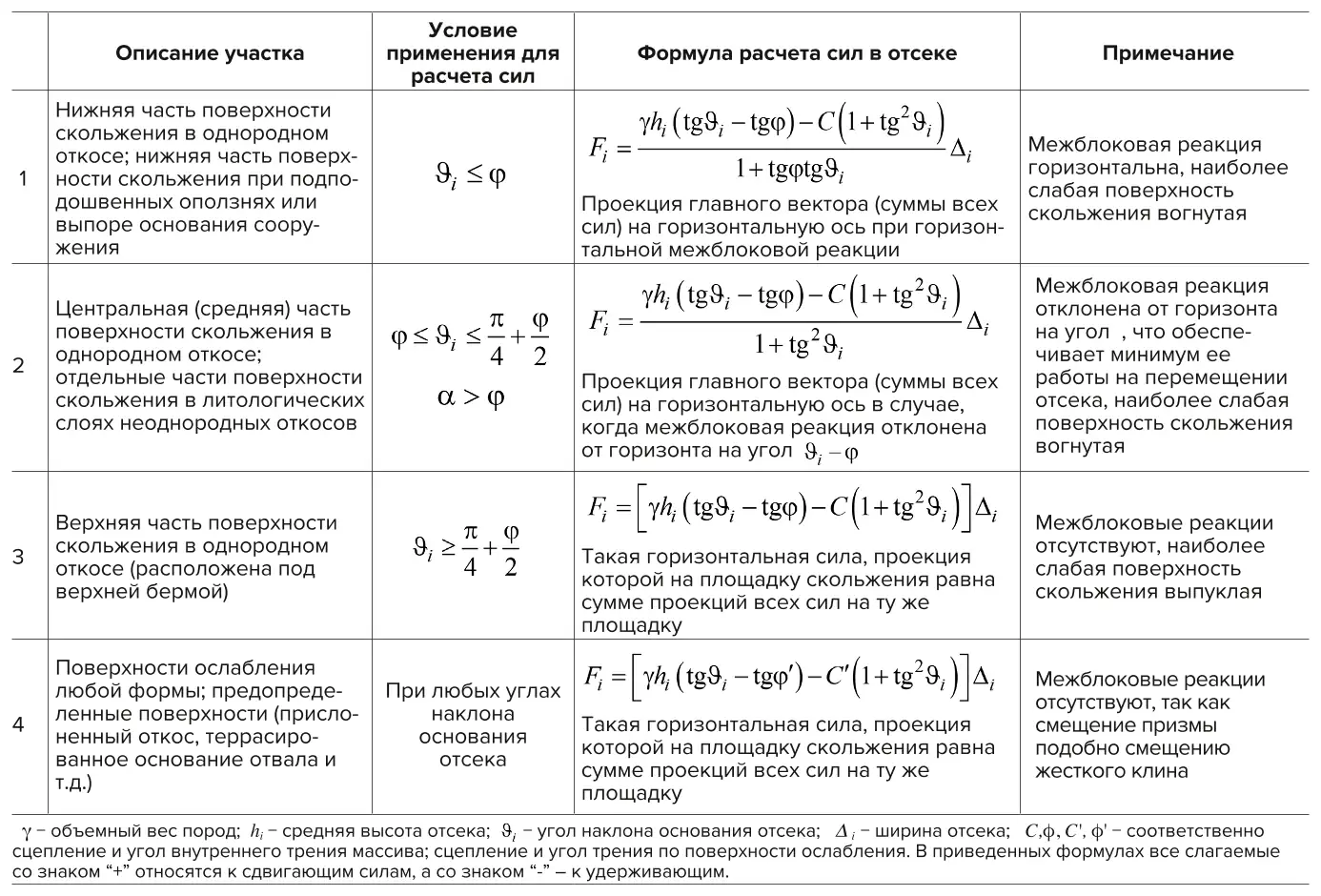

Математический аппарат для установления геометрии наиболее опасной поверхности скольжения в различных горно-геологических условиях и ее построения, а также определения предельных параметров откосов приводится в работе [19].

Необходимо отметить, что вариационный метод, в отличие от способов, реализуемых в программах (инженерных), позволяет сразу в процессе расчета определить предельные параметры опасной поверхности скольжения и предельные параметры откоса. То есть нет необходимости в последовательном итерационном изменении параметров модели откоса с целью нахождения ее предельных параметров (последовательные приближения). Также крайне важно отметить, что при поиске решения уравнений, входящих в вариационный метод, отсутствие корней уравнений напрямую указывает на то, что схема разрушения откоса с данными конкретными принятыми параметрами откоса и физико-механическими характеристиками пород (грунтов) не реализуется. При использовании вариационного метода расчета устойчивости помимо нагрузки от собственного веса сооружения учитываются также нагрузка от оборудования, сейсмическая нагрузка и нагрузка от обводнения сооружения. Может быть также учтена пригрузка породным отвалом (контрфорс).

Таблица 2 Основные схемы расчета устойчивости откосных сооружений согласно вариационному методу

Table 2 Basic schemes for calculating the stability of slope structures using the variational method

В табл. 2 приводятся типовые расчетные схемы для оценки устойчивости откосов и закономерности формирования поверхностей скольжения в различных условиях, полученные на основе вариационного метода. Цифрами в расчетных схемах указываются номера формул из табл. 1, которые необходимо использовать на конкретном участке поверхности скольжения для вычисления обобщенной силы (разности сдвигающих и удерживающих сил). В табл. 2: C, φ ‒сцепление и угол внутреннего трения пород тела откоса (отвала, дамбы и т.д.); C', φ' ‒ сцепление и угол трения по поверхности ослабления (контакту) либо пород основания, в зависимости от расчетной схемы; α ‒ угол откоса; β ‒ угол падения слабого контакта либо контакта пород откоса и основания. При использовании для расчета пологих откосов (α < φ) вариационного метода было выявлено, что поверхность скольжения при отсутствии пригрузки на берме выходит в верхнюю бровку откоса или вообще в откос при соответствующей степени обводнения призмы смещения (форме депрессионной кривой). Таким образом, возможным и достаточно вероятным механизмом потери устойчивости обводненных дамб и отвалов является их разрушение сначала в нижней наиболее обводненной части, а затем вследствие перераспределения напряжений на верхнюю часть поверхности скольжения с полной потерей устойчивости вдоль всей поверхности скольжения. Этому также имеются подтверждения на практике.

Выводы

Проведенные исследования доказывают безальтернативность научного подхода при оценке устойчивости откосов различных сооружений и недопустимость прагматичных (инженерных) методов определения их предельных параметров. Расчеты с использованием предлагаемой теории (вариационный метод) прогнозируют минимальные предельные параметры для однородных, анизотропных и откосов на слабом основании, в подавляющем большинстве случаев расхождения достаточно значительные. Таким образом, ее использование значительно повышает надежность определения предельных параметров откосов и прогноза схем потери устойчивости и параметров призм смещения.

Список литературы

1. Бахаева С.П., Гурьев Д.В. Оценка устойчивости борта котлована под промышленную площадку шахты. Горный информационно-аналитический бюллетень. 2021;(1):32–42. https://doi.org/10.25018/0236-1493-2021-1-0-32-42 Bakhaeva S.P., Gur’ev D.V. Slope stability analysis of pit wall meant for mine infrastructure site. Mining Informational and Analytical Bulletin. 2021;(1):32–42. (In Russ.) https://doi.org/10.25018/0236-1493-2021-1-0-32-42

2. Кутепов Ю.И., Васильева А.Д. Инженерно-геологические условия внешнего отвалообразования на разрезах Кузбасса. Горный информационно-аналитический бюллетень. 2017;(10):122–131. https://doi.org/10.25018/0236-1493-2017-10-0-122-131 Kutepov Yu.I., Vasil’eva A.D. Geotechnical conditions of external dumping at open pit mines in Kuzbass. Mining Informational and Analytical Bulletin. 2017;(10):122–131. (In Russ.) https://doi.org/10.25018/0236-1493-2017-10-0-122-131

3. Шпаков П.С., Юнаков Ю.Л. Устойчивость отвалов на месторождении «Эльдорадо». Горный информационно-аналитический бюллетень. 2018;(6):69–79. https://doi.org/10.25018/0236-1493-2018-6-0-69-79 Shpakov P.S., Yunakov Yu.L. Dump stability at the Eldorado deposit. Mining Informational and Analytical Bulletin. 2018;(6):69– 79. (In Russ.) https://doi.org/10.25018/0236-1493-2018-6-0-69-79

4. Гальперин А.М., Кутепов Ю.И., Еремин Г.М. Методы определения параметров отвалов и технологии отвалообразования на склонах. М.: Горная книга; 2012. 104 с.

5. Kutepov Yu.I., Kutepova N.A., Kutepov Yu.Yi., Vasileva A.D., Mukhina A.S., Smirnov R.D. Engineering-geological and geoecological aspects of formation of dry dumps on hydrodumps. IOP Conference Series: Earth and Environmental Science. 2021;938:012007. https://doi.org/10.1088/1755-1315/938/1/012007

6. Karablin M., Gurev D., Prostov S. Automated stability analysis of soil slopes. E3S Web of Conferences. 2019;105:01015. https://doi.org/10.1051/e3sconf/201910501015

7. Rybin V.V., Konstantinov K.N., Nagovitsyn O.V. Structure of integrated stability monitoring in open pit mining using digital technologies. Journal of Mining Science. 2021;57(4):601–606. https://doi.org/10.1134/S1062739121040074

8. Rybin V.V., Konstantinov K.K., Kagan M.M., Panasenko I.G. The organizing principles of the integrated slope stability monitoring. In: 20th International Multidisciplinary Scientific GeoConference SGEM 2020, Albena, 18–24 August, 2020. Sofia; 2020, pp. 333–338. https://doi.org/110.5593/sgem2020/1.2/s03.043

9. Zhabko A., Volkomorova N., Zhabko N. Theoretical basis for calculation of the quarries sides for collapse. E3S Web of Conferences. 2020;177:01004. https://doi.org/10.1051/e3sconf/202017701004

10. Deng D.-P., Liang L., Zhao L.-H. Limit equilibrium method (LEM) of slope stability and calculation of comprehensive factor of safety with double strength-reduction technique. Journal of Mountain Science. 2017;14(11):2311–2324. https://doi.org/10.1007/s11629-017-4537-2

11. Tianwen Z., Qingxiang C., Liu H., Jisen S., Wei Z. 3D stability analysis method of concave slope based on the Bishop method. International Journal of Mining Science and Technology. 2017;27(2):365–370. https://doi.org/10.1016/j.ijmst.2017.01.020

12. Xie M., Wang Z., Liu X., Xu B. Three-dimensional critical slip surface locating and slope stability assessment for lava lobe of Unzen volcano. Journal of Rock Mechanics and Geotechnical Engineering. 2011;3(1):82–89. https://doi.org/10.3724/SP.J.1235.2011.00082

13. Read J., Stacey P. (eds). Guidelines for open pit slope design. CSIRO; 2009. 496 p. https://doi.org/10.1071/9780643101104

14. Abramson L.W., Lee T.S., Sharma S., Boyce G.M. Slope stability and stabilization methods. 2nd ed. New York: John Wiley & Sons; 2001. 736 p.

15. Hall D.E., Long M.T., Remboldt M.D. (eds). Slope Stability reference guide for national forests in the United States. Washington, DC: U.S. Department of Agriculture, U.S. Forest Service, Engineering Staff; 1994. 3 volumes, 1091 p. Available at: https://forest.moscowfsl.wsu.edu/cgi-bin/engr/library/searchpub.pl?pub=1994e (accessed: 06.06.2024).

16. Гольдштейн М.Н., Кушнер С.Г., Шевченко М.И. Расчеты осадок и прочности оснований зданий и сооружений. Киев: Будiвельник; 1977. 208 с.

17. Соловьев Ю.И. Устойчивость откосов из гипотетического грунта. В кн.: Никитенко Ф.А. (ред.) Вопросы инженерной геологии, оснований и фундаментов. Новосибирск: НИИЖТ; 1962. Вып. 28. С. 83–97.

18. Жабко А.В. Аналитическая геомеханика. Екатеринбург: Изд-во УГГУ; 2016. 224 с. Режим доступа: https://www.geokniga.org/bookfiles/geokniga-zhabkoavanaliticheskayageomehanika.pdf (дата обращения: 06.06.2024).

19. Жабко А.В. Новая концепция оценки устойчивости откосов. Горный информационно-аналитический бюллетень. 2022;(10):104–124. https://doi.org/10.25018/0236_1493_2022_10_0_104 Zhabko A.V. A new concept of slope stability design. Mining Informational and Analytical Bulletin. 2022;(10):104–124. (In Russ.) https://doi.org/10.25018/0236_1493_2022_10_0_104