Моделирование влияния открытых горных работ на состояние нижележащего массива при планировании отработки подземным способом с применением программного комплекса CAE Fidesys
 И.В. Гладков1, Е.Н. Якунчиков1, А.Е. Румянцев2, М.А. Соннов3
И.В. Гладков1, Е.Н. Якунчиков1, А.Е. Румянцев2, М.А. Соннов3
1 АО «СУЭК», г. Новосибирск, Российская Федерация
2 ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация
3 ООО «Фидесис», г. Москва, Российская Федерация
Горная Промышленность №4 / 2024 стр.165-172
Резюме: Применение численного моделирования быстропротекающих процессов при решении задач в масштабах месторождения остается актуальной научной и исследовательской проблемой. Наблюдения за влиянием на массив горных пород, расположенный под ранее отработанными открытым способом запасами, проводить невозможно. Возможны два пути изучения, заключающиеся в физическом и компьютерном (численном) моделировании. Применение физического моделирования требует лабораторной базы и значительных финансовых затрат и является менее предпочтительным для изучения процессов, протекающих при ведении взрывных работ в массиве, находящемся на глубине, но в котором ещё не ведутся подземные горные работы и нет возможности прямого измерения сейсмического сигнала от взрывных работ. Применение бурения с поверхности с установкой глубинных датчиков также требует значительных финансовых затрат и его не всегда возможно предусмотреть, так как работы могут быть разнесены во времени на десятки лет и ранее отработка подземным способом не планировалась. Стоимость выполнения исследований с применением численного моделирования значительно дешевле и помимо высокой квалификации специалиста требует только наличия программного обеспечения и производительного расчётного компьютера. В статье приведен пример применения численного моделирования с применением ПО CAE Fidesys с целью определения влияния технологических факторов при отработке открытым способом на горнотехнические условия отработки запасов пласта Полысаевский в условиях шахты им. А.Д. Рубана. Для формирования модели применен комплексный подход, от оптимизации геометрии взрывных скважин до выполнения пошагового расчета и анализа полученных результатов. Благодаря использованному подходу удалось получить качественную и количественную картину распределения деформаций массива в районе расположения пласта Полысаевский-2 от воздействия ранее осуществленных буровзрывных работ на поверхности.
Ключевые слова: уголь, буровзрывные работы, горные работы, горные породы, методы анализа, сейсмическое воздействие, численная модель, напряженно-деформированное состояние, деформации, пласт, система отработки
Для цитирования: Гладков И.В., Якунчиков Е.Н., Румянцев А.Е., Соннов М.А. Моделирование влияния открытых горных работ на состояние нижележащего массива при планировании отработки подземным способом с применением программного комплекса CAE Fidesys. Горная промышленность. 2024;(4):165–172. https://doi.org/10.30686/1609-9192-2024-4-165-172
Информация о статье
Поступила в редакцию: 07.06.2024
Поступила после рецензирования: 09.07.2024
Принята к публикации: 16.07.2024
Информация об авторах
Гладков Иван Владимирович – инженер по планированию горных работ, АО «СУЭК», г. Новосибирск, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Якунчиков Евгений Николаевич – кандидат технических наук, начальник управления технических сервисов подземных горных работ, АО «СУЭК», г. Новосибирск, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Румянцев Александр Евгеньевич – кандидат технических наук, главный специалист лаборатории геотехники, ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация; ORCID: 0000-0002-2204-961X; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Соннов Максим Александрович – действительный член Академии горных наук, заместитель генерального директора по продажам, ООО «Фидесис», г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Введение
Отработка запасов угля подземным способом в непосредственной близости от участка открытых горных работ может быть осложнена производственной деятельностью карьера (разреза). Это связано с техническими и технологическими операциями при ведении добычных работ, которые могут приводить к ухудшению горно-геологических и горнотехнических условий при последующей отработке запасов шахтой.
При производстве открытых горных работ массив подвергается перераспределению напряжения в связи с выемкой и перемещением значительных объемов горной породы, а также воздействием сейсмической волны от массовых взрывов. При этом в случае начала подземных горных работ после завершения открытых исключается возможность инструментального замера параметров воздействия на горный массив непосредственно на уровне отработки шахтой. В данном случае параметры воздействия можно оценить только расчётными методами.
Перераспределение напряжения ранее рассматривалось только в отношении подземных производственных объектов (приконтурный массив и крепь горных выработок, целики, выработанное пространство и др.). Для оценки влияния взрывных работ на горный массив наиболее используемым является метод определения размеров зон необратимых деформаций (радиус полости R0, радиусы зон разрушения R* и наведенной трещиноватости R1) [1]:
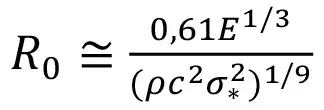 ;(1)
;(1)
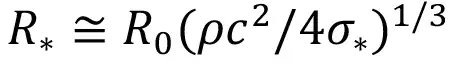 ; (2)
; (2)
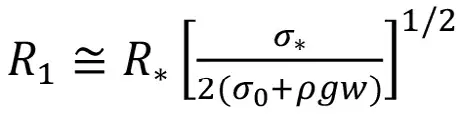 .(3)
.(3)
Одним из основных недостатков данного метода является то, что рассматриваемый массив распространения сейсмической волны представляется как однородная среда. В дополнение в настоящее время накоплено значительное количество экспериментальных данных, свидетельствующих о наличии необратимых проявлений при взрывном воздействии и последующем деформировании массива горных пород в области, радиус которой существенно превосходит расчетные размеры зон необратимых деформаций [1]. В работе [2] с использованием метода динамической фотоупругости изучается взрывное воздействие, связанное с взаимодействием между волнами напряжений от взрыва и распространяющейся трещиной. Результаты показывают, что волны напряжений влияют на локальное поле напряжений в динамической вершине трещины и изменяют характер распространения трещины.
Вопрос влияния взрывных работ на сохранность сооружений, в том числе и горного массива, является актуальной проблемой для многих предприятий и широко освещается в научно-технической литературе [3–6]. Однако изучение в глубине массива такими методами невозможно.
Одним из методов, который позволяет произвести расчеты изменения физических параметров с учетом индивидуальных особенностей структурно-тектонического строения массива, внешних условий и режима протекания процесса, является метод конечных элементов (МКЭ). Так, в работе [7] проведен анализ адекватности применения МКЭ для решения задач взрывного превращения, а основной целью являлось определение областей разрушения вокруг скважины и характера распределения полей различных физических величин. С применением МКЭ в работе [8] оценено влияние сейсмического воздействия взрывных работ в ближней зоне.
В работе [9] приведен пример формирования численной модели, основной задачей которой является прогнозирование поведения массива горных пород под воздействием взрыва, в том числе определение степени повреждения, размера и формы выемки, смещения массива горных пород, распределения напряжений и деформаций. Указывается, что применение таких моделей дает положительный экономический эффект при отработке месторождений полезных ископаемых.
С применением численного моделирования путём объединения различных подходов в работе [10] решается задача формирования трещин и их прочности на микрометрическом уровне.
В работе [11] предложен подход к определению скоростей смещения и деформаций массива с применением численного моделирования в программе ANLOG с помощью метода конечных элементов.
Методы численного моделирования успешно применяются зарубежными и отечественными специалистами при изучении взрывного разрушения горных пород [12–14].
В плане механики горных пород довольно трудно прогнозировать изменения напряженно-деформированного состояния массива после динамического нагружения слоистых пород, имеющих разные, серьезно отличающиеся прочностные свойства. Примером таких массивов могут служить месторождения угля. Решать подобные задачи численными методами представляется наиболее целесообразным.
Основная идея МКЭ состоит в том, что любую непрерывную величину можно аппроксимировать дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определённых на конечном числе подобластей (элементов), при этом кусочно-непрерывные функции определяются с помощью значений непрерывной величины в конечном числе точек рассматриваемой области. Однако данный метод требует значительного количества производимых расчетов, что достигается посредством вычислительной техники и специально составленных вычислительных программ.
В данной работе рассмотрен опыт решения вышеприведенных задач посредством программного комплекса CAE Fidesys.
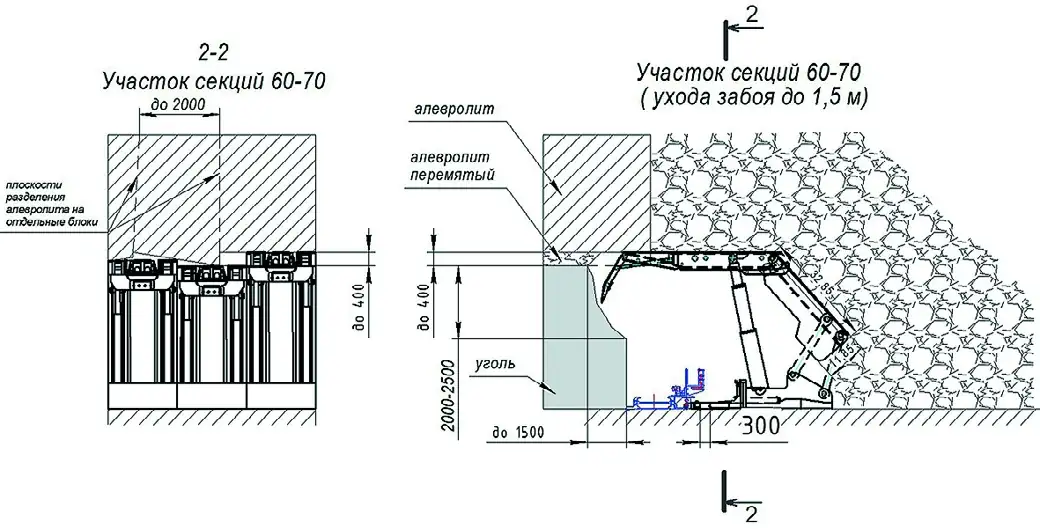 Рис. 1 Лава №807 угольного пласта Полысаевский-2
Рис. 1 Лава №807 угольного пласта Полысаевский-2
Fig. 1 Longwall face No. 807 of the Polysaevsky-2 coal seam
На шахте им. А.Д. Рубана с августа 2023 г. происходит снижение скорости подвигания очистного забоя лавы №807 угольного пласта Полысаевский-2 вследствие куполообразования, что связано с резким уменьшением прочности и устойчивости горных пород (рис. 1). Локация куполообразования располагается под ранее отработанным открытым способом участком вышележащего пласта (рис. 2), при этом подземные горные работы были начаты по завершении открытых. Согласно методике расчетов зоны необратимой деформации (R0, R*, R1) рассматриваемый пласт находится за её пределами.
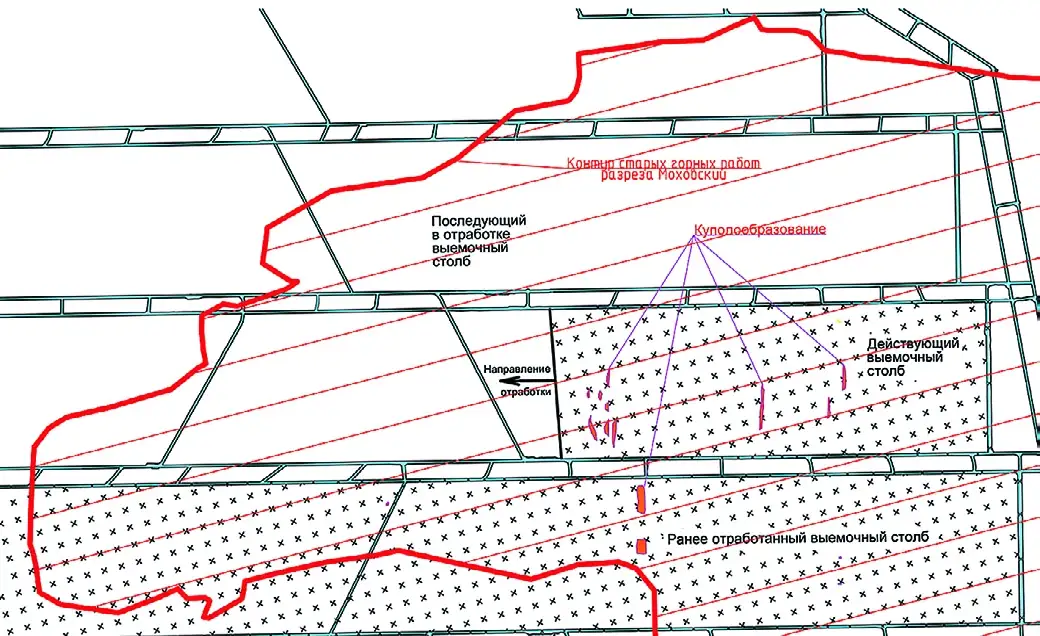 Рис. 2 Схема локации куполообразования под ранее отработанным открытым способом участком вышележащего пласта
Рис. 2 Схема локации куполообразования под ранее отработанным открытым способом участком вышележащего пласта
Fig. 2 A schematic representation of doming under the overlying seam section that was previously worked out by the surface mining method
Поставленные задачи
Посредством программного комплекса CAE Fidesys произведено решение следующих задач:
1. Определение влияния подвигания забоя и формирования отвала разреза «Моховский» на разупрочнение угольного пласта Полысаевский-2 и вмещающих пород.
2. Определение влияния взрывных работ разреза «Моховский» на разупрочнение угольного пласта Полысаевский-2 и вмещающих пород.
Подходы к решению поставленных задач
1. Ранее в CAE Fidesys решались задачи по рассмотрению процесса нарушения массива, прилегающего к контуру горных выработок, путем выявления участков, в которых напряжения приводили к пластическим деформациям при решении в упругопластической постановке или через коэффициент запаса прочности при решении в упругой постановке. В данном случае рассматривается частичное разрушение нетронутого массива, находящегося в условиях гидростатического напряжения напрямую через параметр «деформация».
2. Для решения задачи о распространении волн был применен метод спектральных элементов (МСЭ) модуля Fidesys Dynamics, который эффективен для расчетов нестационарных задач с быстропротекающими процессами, требующих особой точности. Эта одна из современных модификаций МКЭ.
Основными преимуществами МСЭ по сравнению с традиционным методом конечных элементов являются более высокая скорость выполнения расчетов, высокая точность аппроксимации искомого решения при относительно небольшом числе элементов. Такой подход позволяет фиксировать деформацию как в период распространения, так и наложения затухающих и отраженных волн.
Моделирование
Модель горного отвода, состоящая из переслаивания осадочных пород, была импортирована из системы автоматизированного проектирования в препроцессор комплекса CAE Fidesys. Значительные размеры модели – 330 м по вертикали на 2500 м по горизонтали – обусловливают решение задачи распространения сейсмовзрывной волны в 2D постановке. В границы модели входит массив горного отвода от дневной поверхности до подстилающих пласт Полысаевский-2 пород. Для исключения влияния граничных условий мощность пород почвы пласта Полысаевский-2 условно увеличиваем до 150 м. Каждый пласт выделяется в отдельный домен. Домены по признаку «тип породы» объединяются в отдельные блоки. Блокам присваиваются соответствующие упруго-прочностные характеристики (табл. 1).
Таблица 1 Физико-механические свойства породы
Table 1 Physical and mechanical properties of the rocks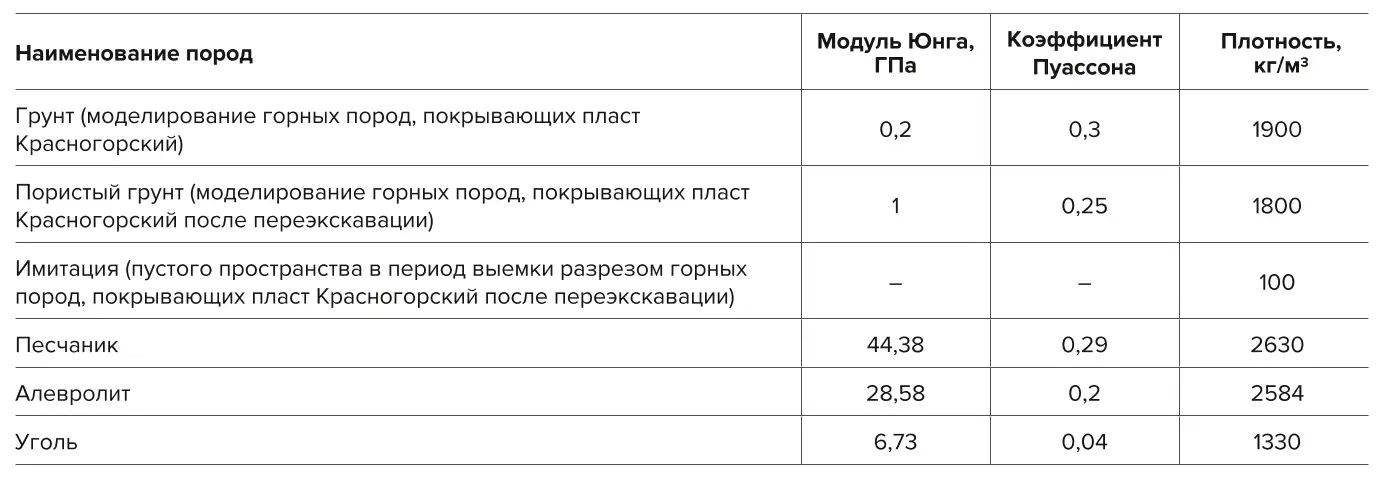
Для моделирования пошагового изменения условий нагружения массива покрывающие отработанный разрезом пласт Красногорский породы разбиты на отдельные объемы, соответствующие отдельному циклу отработки (выемки и переэкскавации пород). Для моделирования воздействия энергии взрывных работ разреза на горный массив в границах одного отдельного объема сформированы скважины, имитирующие взрывные работы (рис. 3). Ввиду моделирования большого числа скважин для уменьшения количества конечных элементов и уменьшения зон концентрации напряжений принята игловидная форма скважин и проверено качество конечно-элементной сети (рис. 4). При генерировании сетки конечных элементов необходимо уделить особое внимание проверке качества сетки на участках выклинивания пластов (рис. 5). Для обеспечения баланса скорости и качества расчётов при моделировании сейсмовзрывных волн принят 4-й порядок элементов в первоначально построенной сетке.
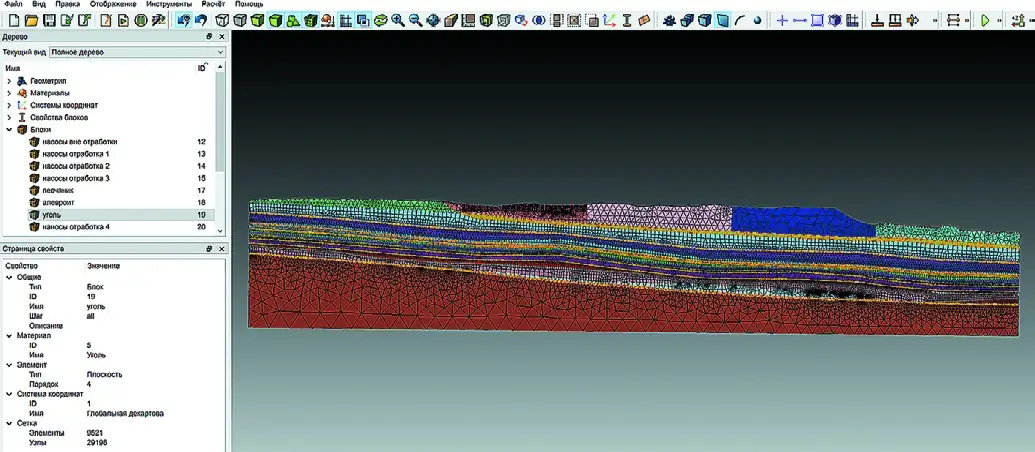 Рис. 3 Представление модели с объёмами извлечения и взрывания
Рис. 3 Представление модели с объёмами извлечения и взрывания
Fig. 3 Representation of the model with the mining and blasting volumes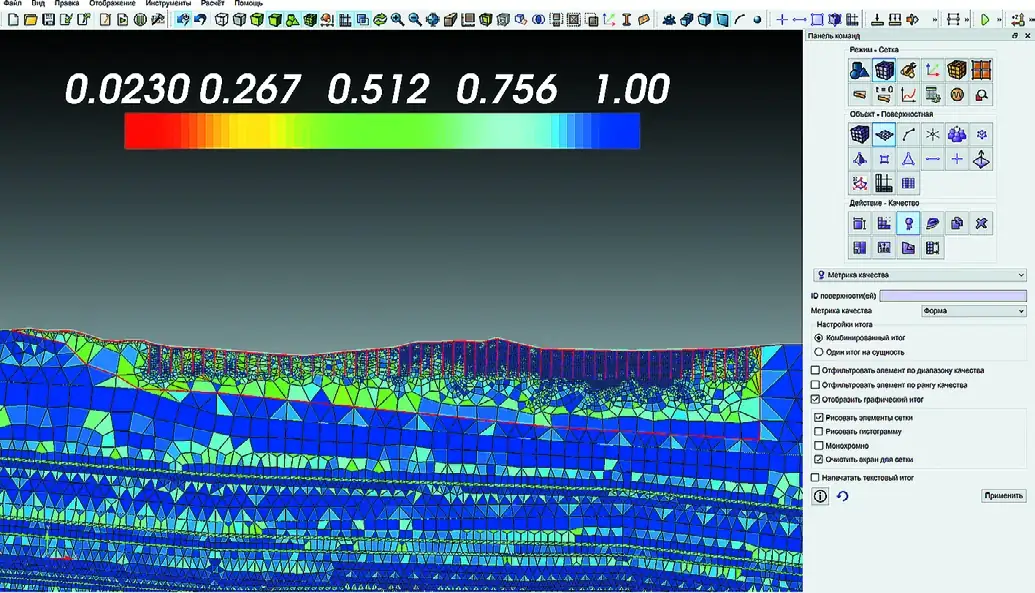 Рис. 4 Формирование скважин и проверка качества конечно- элементной сети
Рис. 4 Формирование скважин и проверка качества конечно- элементной сети
Fig. 4 Creation of the boreholes and verification of the finite element network quality Рис. 5 Проверка качества конечно- элементной сети в местах выклинивания пластов
Рис. 5 Проверка качества конечно- элементной сети в местах выклинивания пластов
Fig. 5 Verification of the finite element network quality in places of seam thinning
Принятие внешних и граничных условий, параметров расчета
Для задачи 1:
– для всей модели задается сила гравитации (для формирования нагрузок в моделях от собственного веса вышележащих пород);
– для нижней границы модели накладывается запрет на перемещение по вертикальному направлению; – для боковых границ модели задаются свойства неотражающих поверхностей (для исключения возникновения разницы напряжения внутри отдельных слоев при боковом распоре);
– в условиях расчета напряженно-деформированного состояния задано 6 шагов нагружения с изменением свойств материала, где до отработки домен имеет свойства грунта, после выемки материала – с 0-ми параметрами (имитация пустого пространства), после переэкскавации – свойства рыхлого грунта (имитация отвала);
– для определения воздействия подвигания забоя разреза на массив осуществлён статический расчет напряженно-деформированного состояния в упругой постановке.
Для задачи 2:
– на стенки скважин прикладывается распределенная сила по зависимости Берлаге с условиями, обеспечивающими параметры на первом положительном полупериоде: давление 22 ГПа с продолжительностью 0,0033 с (для имитации детонации ВВ без зазора между ВВ и стенками скважин со скоростью 6000 м/с) (рис. 6);
 Рис. 6 Имитация давления на стенки скважины в ПО Fidesys
Рис. 6 Имитация давления на стенки скважины в ПО Fidesys
Fig. 6 Simulation of borehole wall pressure in the Fidesys software suite
– воздействие гравитации отлючается (для исключения деформаций от собственного веса вышележащих пород, при этом свойства распространения волны не изменятся);
– при моделировании волнового воздействия границам модели присваиваются неотражающие поверхности, но ввиду значительности габаритов модели и недостижения волнами со значительной амплитудой границ модели данным условием можно пренебречь и присвоить стандартные граничные условия;
– для определения воздействия сейсмовзрывной волны на массив осуществляется расчет временного анализа.
Анализ результатов
Основной задачей рассматриваемого моделирования является определение степени разупрочнения подземных горных пород под влиянием горных работ разреза, то есть увеличения в размерах существующих систем трещин и формирования новых. Развитие трещин в массиве происходит при смещении соседних точек массива.
Выбор в качестве критерия «смещение» может быть непоказательным, поскольку отражает смещение соседних точек в одном и том же направлении относительно первоначального их положения. Деформация – изменение формы и размеров массива, связанное с перемещением друг относительно друга соседних точек. По вышеизложенным соображениям в качестве критерия степени влияния горных работ разреза на разупрочнение массива при ведении подземных горных работ принята «деформация». Для наглядности в шкале деформаций в анализе результатов выделены отдельные спектры для диапазонов значений: синий – от 0 до 10–4 (уровень деформации, при котором не происходит нарушения целостности горного массива [1]); фиолетовый – от 10–4 до 0,001; бирюзовый – от 0,001 до 0,04; зеленый – от 0,04 до 0,1; желтый – от 0,1 до 1; красный – от 1 до предельного значения.
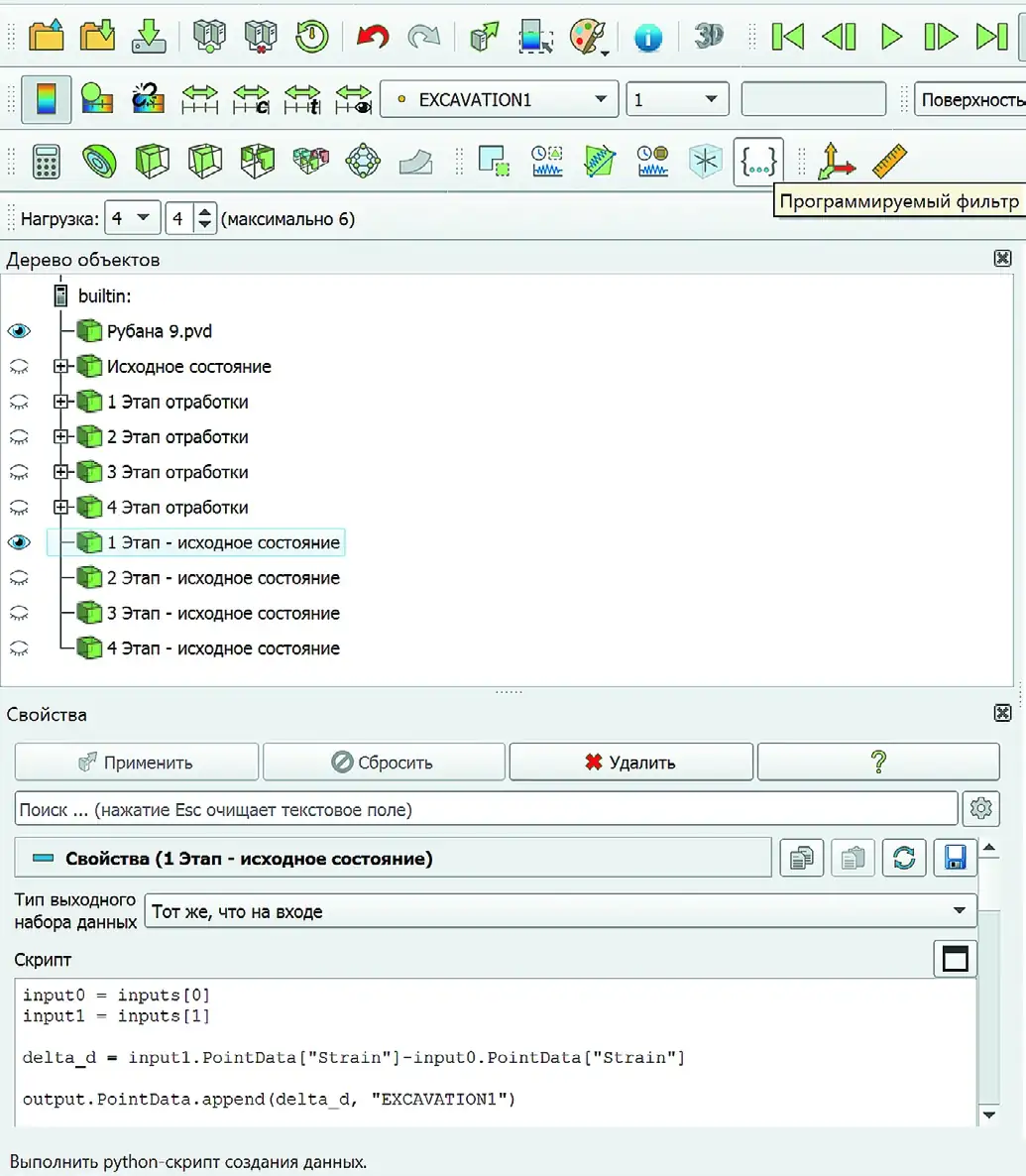 Рис. 7 Код для исключения из полученных результатов величины первоначальной деформации
Рис. 7 Код для исключения из полученных результатов величины первоначальной деформации
Fig. 7 Code for excluding initial deformation value from the results obtained
Для задачи 1. С использованием кода (рис. 7) для программируемого фильтра в ПО Fidesys Viewer производится исключение из полученных результатов величины первоначальной деформации от первого расчётного шага, когда модель получает природное напряженное состояние. По результатам моделирования пошагового подвигания борта разреза деформации пласта Полысаевский-2 получены величины деформаций со значениями от 10–4 до 0,001. При таких значениях деформаций естественные трещины могут раскрываться, что будет оказывать негативное влияние на устойчивость при ведении подземных горных работ (рис. 8–11).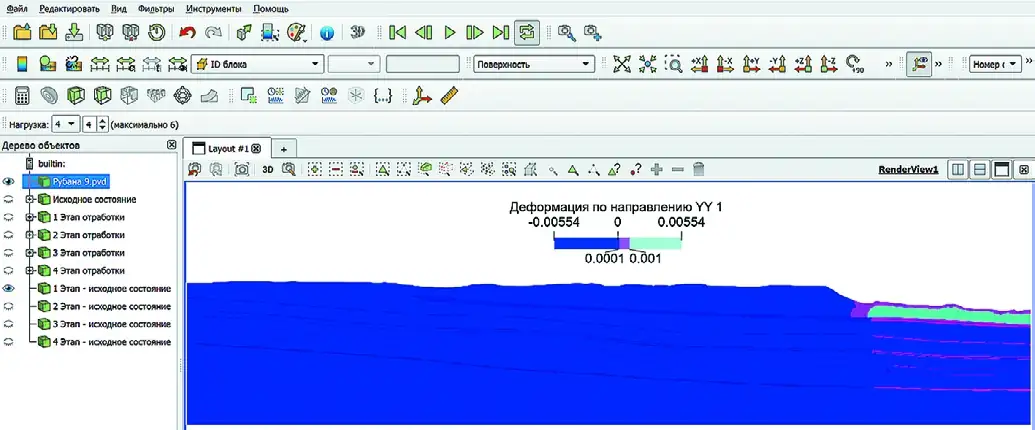 Рис. 8 Первый шаг отработки разрезом пласта Красногорский
Рис. 8 Первый шаг отработки разрезом пласта Красногорский
Fig. 8 The first step in strip mining of the Krasnogorsky coal seam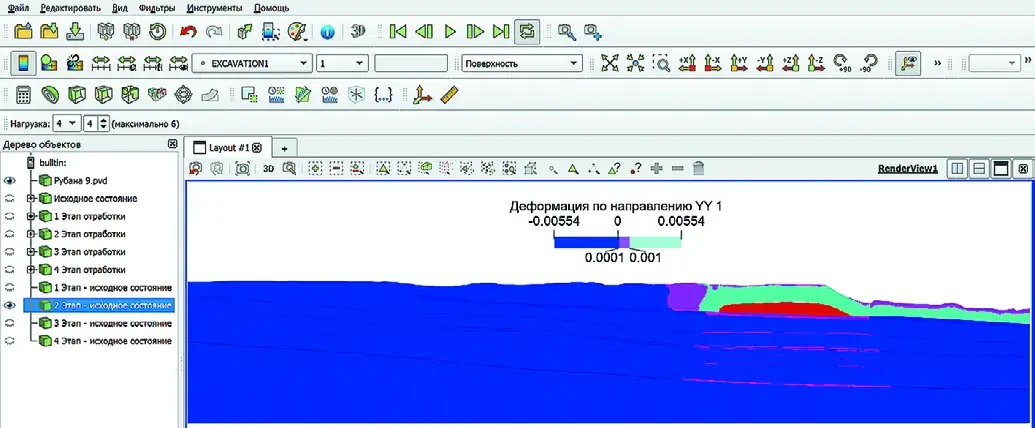 Рис. 9 Второй шаг отработки разрезом пласта Красногорский
Рис. 9 Второй шаг отработки разрезом пласта Красногорский
Fig. 9 The second step in strip mining of the Krasnogorsky coal seam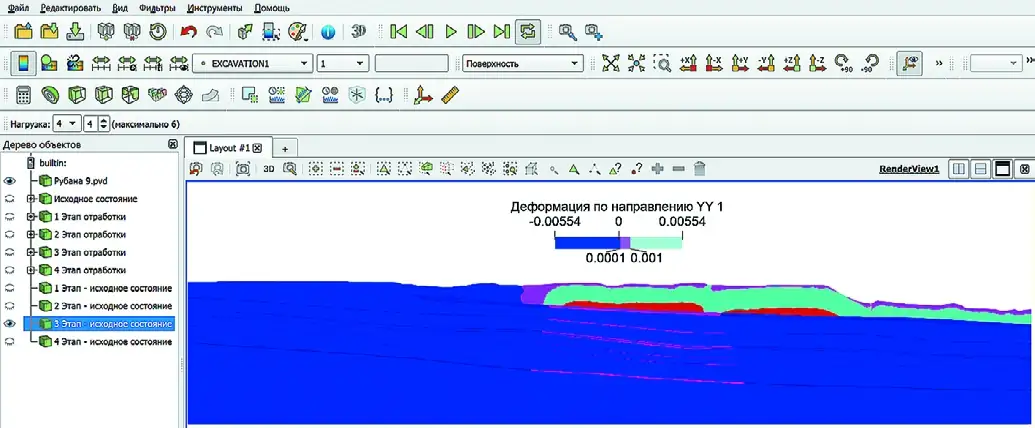 Рис. 10 Третий шаг отработки разрезом пласта Красногорский
Рис. 10 Третий шаг отработки разрезом пласта Красногорский
Fig. 10 The third step in strip mining of the Krasnogorsky coal seam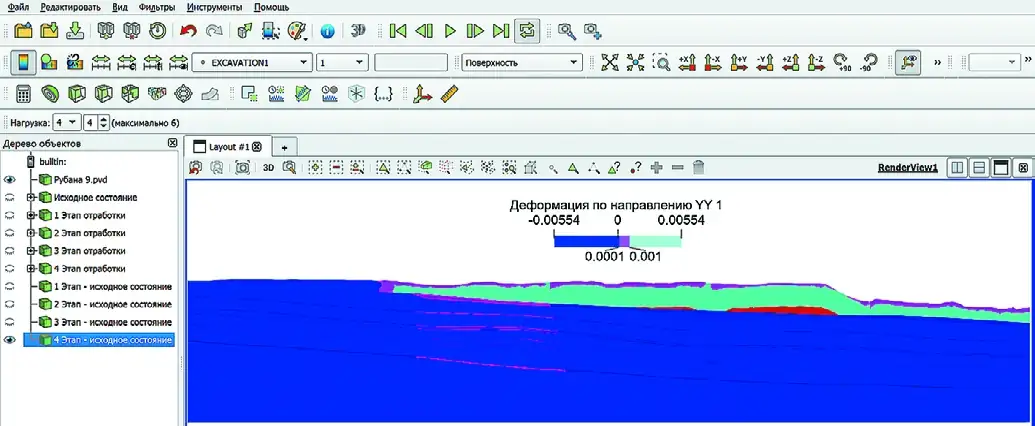 Рис. 11 Четвёртый шаг отработки разрезом пласта Красногорский
Рис. 11 Четвёртый шаг отработки разрезом пласта Красногорский
Fig. 11 The fourth step in strip mining of the Krasnogorsky coal seam
Для задачи 2. Основной массив деформации ограничен по глубине в пределах пород до первого угольного пласта Красногорский (демпфер-экрана) (рис. 12–14), ниже которого происходит распределение среднего уровня деформации с резким увеличением в пределах угольных пластов, в том числе Полысаевского-2. Это связано с проходом и отражением сейсмических волн на границах раздела сред, изменением упруго-прочностных свойств и формированием разницы значений главных напряжений (увеличение девиатора напряжений) из-за одновременного взрывания большого количества ВВ (с порядным замедлением, в модели рассмотрено одновременное взрывание одного ряда скважин). При этом стоит отметить, что уровни деформации от 10–4 до 0,001 при взрывных работах отмечаются на временном промежутке после завершения детонации заряда (0,003 с) и прохождения первичной сейсмической волны (0,03 с для глубины 200 м, соответствующей горизонту пласта Полысаевский-2) (см. рис. 12–14). Деформации более 0,001 с зафиксированы в период распространения и наложения затухающих и отраженных волн. На рисунках отчётливо видна неравномерность распространения сейсмовзрывных волн, связанная с неравномерной слоистой структурой массива.
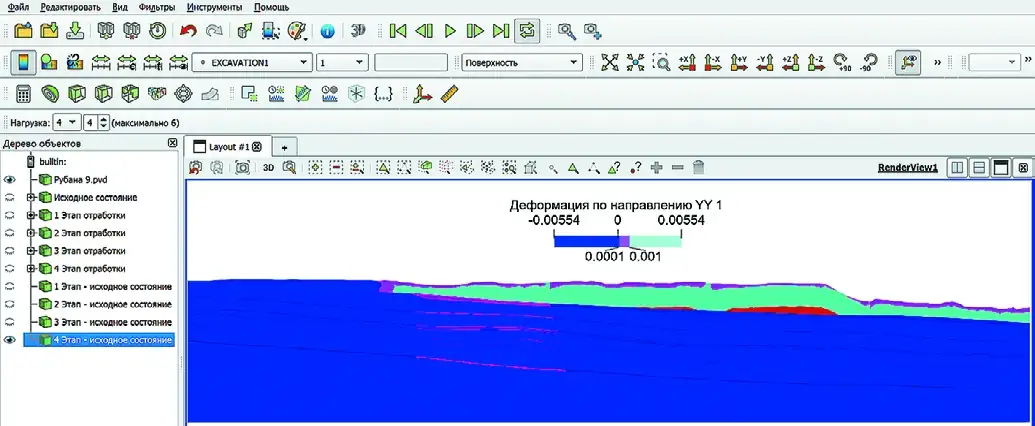 Рис. 12 Временной интервал 0,03 с
Рис. 12 Временной интервал 0,03 с
Fig. 12 Time span of 0.03 s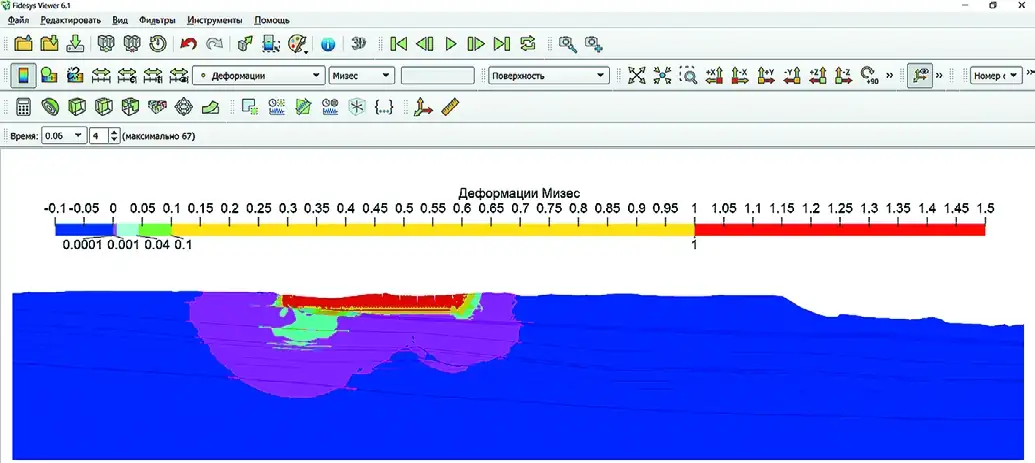 Рис. 13 Временной интервал 0,06 с
Рис. 13 Временной интервал 0,06 с
Fig. 13 Time span of 0.06 s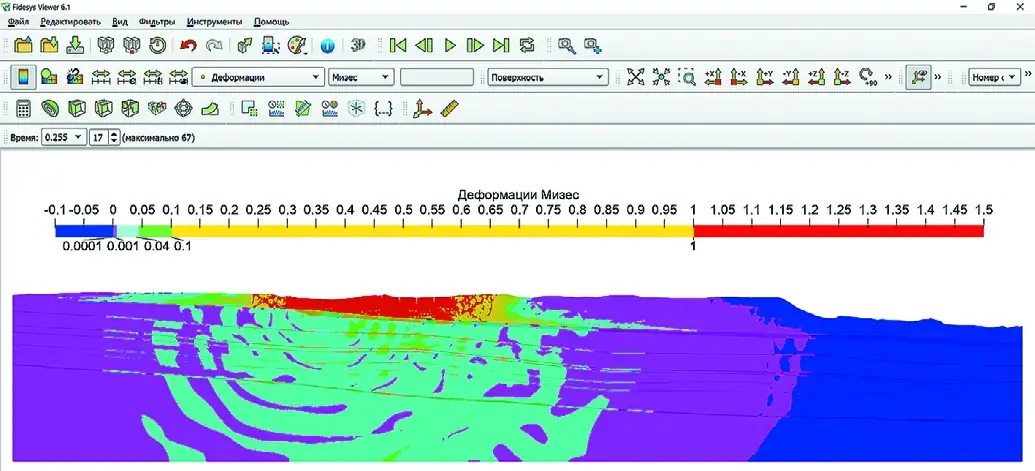 Рис. 14 Временной интервал 0,255 с
Рис. 14 Временной интервал 0,255 с
Fig. 14 Time span of 0.255 s
Выводы
1. В результате численного моделирования подтверждено, что наличие слоев в горной породе приводит к неоднородному распространению волн. Это выражается в снижении скорости распространения, но также приводит к увеличению деформаций из-за возможной интерференции волн.
Для определения степени нарушенности горного массива от воздействия открытых горных работ, в том числе взрывных работ, посредством программного комплекса CAE Fidesys установлена возможность оценки критического уровня деформации. Результаты, полученные при моделировании, коррелируют с наблюдаемой в шахтных условиях ситуацией при ведении горных работ.
Основной задачей такой модели является прогнозирование поведения массива горных пород под воздействием взрыва, в том числе определение степени повреждения через деформации.
Используемая численная модель обеспечивает комплексный и экономичный подход к анализу процессов на инженерном уровне и является одним из эффективных способов оценки состояния сложноструктурного массива с учетом динамического нагружения, поскольку позволяет изучить различные физические поля и определить степень нарушения в интересующей области модели (пласта).
2. Для определения изменений в массиве, происходящих под влиянием техногенных воздействий, можно, используя программируемый фильтр (сценарии python) в постпроцессоре CAE Fidesys, который позволяет исключить изменения в массиве при первичном наложении внешних условий, таких как гравитация.
Дополнительный модуль Fidesys Dynamics расширяет функционал CAE Fidesys возможностью расчетов нестационарных задач с быстропротекающими процессами, требующих особой точности, методом спектральных элементов как математический аппарат для описания воздействия взрывной волны в сложной блочной системе. Поскольку превышения критического уровня деформации горного массива зафиксированы в период распространения и наложения затухающих и отраженных волн, CAE Fidesys позволяет выявить необратимые проявления при взрывном деформировании массива горных пород в области, радиус которых существенно превосходит величину, рассчитанную согласно традиционной методике.
Список литературы
1. Садовский М.А. Избранные труды. Геофизика и физика взрыва. М.: Наука; 2004. 440 с. Режим доступа: https://www.geokniga.org/books/21916 (дата обращения: 21.05.2024).
2. Xu P., Yang R.-S., Guo Y., Chen C., Kang Y. Investigation of the effect of the blast waves on the opposite propagating crack. International Journal of Rock Mechanics and Mining Sciences. 2021;144:104818. https://doi.org/10.1016/j.ijrmms.2021.104818
3. Верхоланцев А.В., Шулаков Д.Ю., Дягелев Р.А. Особенности оценки сейсмического воздействия буровзрывных работ. Горный журнал. 2019;(5):29–35. https://doi.org/10.17580/gzh.2019.05.05 Verkholantsev A.V., Shulakov D.Yu., Dyagilev R.A. Features of assessing seismic effects of blasting operations. Gornyi Zhurnal. 2019;(5):29–35. (In Russ.) https://doi.org/10.17580/gzh.2019.05.05
4. Холодилов А.Н., Господариков А.П, Еременко А.А. Методические основы классификации взрывов по уровню их сейсмического действия. Горный журнал. 2021;(5):98–102. https://doi.org/10.17580/gzh.2021.05.13 Kholodilov A.N., Gospodarikov A.P., Eremenko A.A. Procedural framework for explosion classification by the seismic load criterion. Gornyi Zhurnal. 2021;(5):98–102. (In Russ.) https://doi.org/10.17580/gzh.2021.05.13
5. Hosseinzadeh Gharehgheshlagh H., Alipour A. Ground vibration due to blasting in dam and hydropower projects. Rudarsko-geološko-naftni zbornik (The Mining-Geology-Petroleum Engineering Bulletin). 2020;35(3):59–66, https://doi.org/10.17794/rgn.2020.3.6
6. Марысюк В.П., Сабянин Г.В., Трофимов А.В., Киркин А.П. Определение параметров скважинных зарядов ВВ при очистной отбойке на основе расчета зон разрушения и районирования руд по физико-механическим свойствам. Горный журнал. 2020;(1):58–62. https://doi.org/10.17580/gzh.2020.01.11 Marysyuk V.P., Sabyanin G.V., Trofimov A.V., Kirkin A.P. Designing blast patterns by calculation of fracture zones and ore zoning by physical and mechanical properties. Gornyi Zhurnal. 2020;(1):58–62. (In Russ.) https://doi.org/10.17580/gzh.2020.01.11
7. Камянский В.Н. Моделирование взрыва скважинных зарядов в среде Ansys. Проблемы недропользования. 2017;(1):119–126. https://doi.org/10.18454/2313-1586.2017.01.119 Kamyansky V.N. Borehole blasting simulation using Ansys software. Problems of Subsoil Use. 2017;(1):119–126. (In Russ.) https://doi.org/10.18454/2313-1586.2017.01.119
8. Камянский В.Н. Оценка сейсмовзрывных нагрузок на законтурный массив при разделке отрезной щели. Горный информационно-аналитический бюллетень. 2018;(7):181–188. https://doi.org/10.25018/0236-1493-2018-7-0-181-188 Kamyansky V.N. Estimation of seismic load of blasting on pit wall rock mass during blasted slot making. Mining Informational and Analytical Bulletin. 2018;(7):181–188. (In Russ.) https://doi.org/10.25018/0236-1493-2018-7-0-181-188
9. Мысин А.В., Ковалевский В.Н. Моделирование состояния сложноструктурного массива с учетом динамического нагружения. Горный журнал. 2024;(5):38–47. https://doi.org/10.17580/gzh.2024.05.03 Mysin A.V., Kovalevskiy V.N. Modeling behavior of complex-structured rock mass with regard to dynamic impact. Gornyi Zhurnal. 2024;(5):38–47. (In Russ.) https://doi.org/10.17580/gzh.2024.05.03
10. Pan C., Li X., Li J., Zhao J. Numerical investigation of blast-induced fractures in granite: insights from a hybrid LS-DYNA and UDEC grain-based discrete element method. Geomechanics and Geophysics for Geo-Energy and Geo-Resources. 2021;7:49. https://doi.org/10.1007/s40948-021-00253-6
11. Toraño J., Rodríguez R., Diego I., Rivas J.M., Casal M.D. FEM models including randomness and its application to the blasting vibrations prediction. Computers and Geotechnics. 2006;33(1):15–28. https://doi.org/10.1016/j.compgeo.2006.01.003
12. Mysin A., Kovalevskiy V. Creation and Verification of Numerical Model of Explosive Charge Blast in The Ansys Software System, for the Purpose of Substantiating the Optimal Parameters of Drilling and Blasting Operations. E3S Web of Conferences. 2020;174:01046. https://doi.org/10.1051/e3sconf/202017401046
13. Onederra I.A., Furtney J.K., Sellers E., Iverson S. Modelling blast induced damage from a fully coupled explosive charge. International Journal of Rock Mechanics and Mining Sciences. 2013;58:73–84. https://doi.org/10.1016/j.ijrmms.2012.10.004
14. Bonet J., Wood R.D. Nonlinear Continuum Mechanics for Finite Element Analysis. 2nd ed. Cambridge: Cambridge University Press; 2008. 318 p. Available at: https://www.klancek.si/sites/default/files/datoteke/files/bonet-woodnonlinearcontinuummechanics2ndedition.pdf (accessed: 21.05.2024).








