Течение вязкой диспергирующей газовоздушной смеси, обусловленное внезапным выбросом газа в рудничную атмосферу

С.В. Черданцев, П.А. Шлапаков, Е.А. Шлапаков, К.С. Лебедев, В.В. Колыхалов
АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли», г. Кемерово, Российская Федерация
Горная Промышленность №5 / 2024 стр.154-159

Резюме: В процессе разработки угольных месторождений образуются выбросоопасные области, склонные к внезапным выбросам угля, породы и газа в горные выработки. Внезапные выбросы приводят к тяжелым авариям, нередко со смертельным исходом. Как правило, выбросы происходят с высокой скоростью, иногда превышающей скорость звука. Выброшенный газ с точки зрения газовой динамики представляет собой возмущение, под действием которого в малоподвижном воздухе рудничной атмосферы формируется ударная волна, интенсивность которой зависит от скорости выброшенного газа. Ударная волна способна нанести травмы рабочим, разрушить крепь горной выработки и вывести из строя механизмы и технологическое оборудование, находящиеся в окрестности выброса. В этой связи задачи о течении газовоздушных смесей, обусловленных внезапными выбросами, представляются весьма актуальными, как с научной, так и с практической точки зрения. В статье рассматривается задача о течении газовоздушных смесей, обладающих вязкими и дисперсионными свойствами, описываемая уравнением в частных производных Кортевега – де Вриза – Бюргерса, решение которого представлено в замкнутом виде. На базе вычислительных процедур построены графики, характеризующие условия течения газовоздушных смесей при различных параметрах их вязкости и дисперсности. Выполнен анализ графиков и выявлен ряд закономерностей течения газовоздушных смесей.

Ключевые слова: горные выработки, внезапные выбросы угля и газа, волновое число, дисперсионная функция, фаза колебаний, групповая скорость, вязкость газовоздушных смесей, уравнение Кортевега – де Вриза – Бюргерса

Для цитирования: Черданцев С.В., Шлапаков П.А., Шлапаков Е.А., Лебедев К.С., Колыхалов В.В. Течение вязкой диспергирующей газовоздушной смеси, обусловленное внезапным выбросом газа в рудничную атмосферу. Горная промышленность. 2024;(5):154–159. https://doi.org/10.30686/1609-9192-2024-5-154-159

Информация о статье

Поступила в редакцию: 15.07.2024

Поступила после рецензирования: 27.08.2024

Принята к публикации: 10.09.2024

Информация об авторах

Черданцев Сергей Васильевич – доктор технических наук, главный научный сотрудник, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), г. Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Шлапаков Павел Александрович – кандидат технических наук, заведующий лабораторией, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), г. Кемерово; Российская Федерация, e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Шлапаков Евгений Александрович – старший научный сотрудник, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), г. Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Лебедев Кирилл Сергеевич – старший научный сотрудник, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), г. Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Колыхалов Виктор Валентинович – старший научный сотрудник, АО «Научный центр ВостНИИ по промышленной и экологической безопасности в горной отрасли» (АО «НЦ ВостНИИ»), г. Кемерово, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

Внезапные выбросы угля и газа на угольных предприятиях происходят регулярно в течение многих десятилетий, практически во всех угледобывающих странах. Механизм внезапных выбросов обусловлен главным образом высоким давлением скопившегося газа в порах, трещинах и пустотах породоугольного массива [1–4]. Выбросы угля, пород и газа сопровождаются не только значительной массой выбрасываемой горной массы и большими объемами газа, но и высокой скоростью выбрасываемого газа. При этом, как показано в работе [5], скорость истечения газа из образовавшейся при выбросе полости зависит от формы полости. Процесс выброса газа можно рассматривать как некоторое возмущение, передающееся в рудничную атмосферу [2; 3]. Поскольку воздушный поток является сжимаемым, то возмущение передается потоку от слоя к слою, создавая тем самым движение газовоздушного потока в виде движущейся волны.

К настоящему времени концепция волнового движения получила достаточно широкое применение во многих областях естествознания и техники и хорошо отражена как в отечественной [6–8], так и в зарубежной литературе [9–12]. Однако в горном деле эта концепция, на наш взгляд, еще не получила достаточного внимания при исследовании важнейших газодинамических процессов в рудничной атмосфере. Поэтому волновые процессы довольно слабо отражены в периодической литературе по горной тематике. Авторы этой статьи предприняли попытку хотя бы частично восполнить этот пробел, в связи с чем рассматривают задачу о течении газовоздушного потока в рудничной атмосфере, обусловленного внезапным выбросом газа, с позиций волновой динамики в рамках следующих допущений:

1) течение газа по горной выработке рассматривается как одномерное;

2) газ является политропным и баротропным, в связи с чем его теплоемкость не меняется, а плотность газа зависит только от давления;

3) предполагается, что внезапные выбросы газа способны сформировать ударные волны средней и малой интенсивности.

Известно, что волновые движения описываются уравнениями в частных производных, решение которых в простейшем одномерном случае представляется в виде [13]

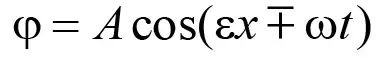, (1)

где φ, A – искомая функция и её амплитудное значение, характеризующие рассматриваемый волновой процесс; x – декартовая координата, направленная вдоль выработки в сторону движения волны; t – время; ω – частота волнового процесса; ε – волновое число, связанное с длиной волны λ следующим образом:

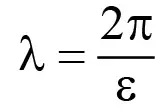. (2)

Знак «минус» в (1) соответствует распространению волны в положительном направлении оси x, а знак «плюс» – в отрицательном. В дальнейшем будем рассматривать волну, движущуюся только в положительном направлении, и поэтому аргументом у тригонометрической функции в формуле (1) будет величина

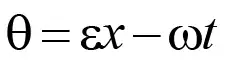, (3)

представляющая собой фазу колебания волны. Если частота ω, волновое число ε и фаза колебаний θ являются постоянными величинами, то, продифференцировав (3) по времени

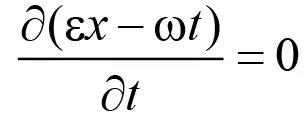, (4)

и обозначая дx/дt = a – фазовую скорость перемещения волны, находим соотношение между угловой скоростью, волновым числом и фазовой скоростью волны

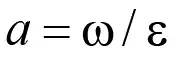, (5)

которое имеет место только в условиях идеальной сплошной среды.

В ряде работ авторов [14; 15] рассмотрены волновые процессы в шахтной перемычке цилиндрической формы при условии, что частота волны, волновое число и фазовая скорость являются постоянными величинами. Однако, несмотря на важность полученных в работах [14; 15] результатов, необходимо отметить их частный характер.

Дело в том, что частота волны ω является в общем случае функцией волнового числа ω = ω(ε), которую называют дисперсионной функцией, а характеризуемую ею волну называют диспергирующей волной. В связи с этим скорость перемещения диспергирующей волны характеризуется не фазовой скоростью a, а групповой скоростью agr, определяемой по формуле [16; 17]

.

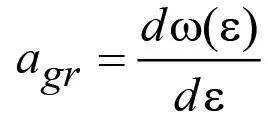К настоящему времени предложен целый ряд функций, аппроксимирующих дисперсионную функцию ω(ε). В данной статье мы будем использовать следующую функцию [16]:

,

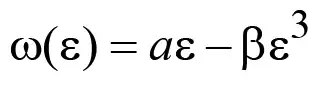которой будет соответствовать групповая скорость

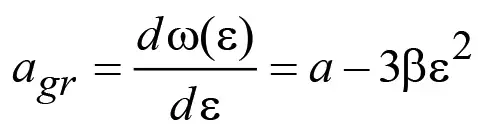, (6)

где β является некоторым параметром, характеризующим дисперсионные свойства рассматриваемой смеси. Если β = 0, то формула (6) вырождается в формулу (5) для идеального газа.

В данной статьей используются не только дисперсионные, но и вязкие свойства газовоздушных смесей, о чем далее будет сказано более подробно.

Построение решения задачи о течении вязкой диспергирующей смеси в горной выработке В силу третьего допущения будем полагать, что течение газовоздушной смеси, сформированное внезапным выбросом газа, представляет собой ударную волну небольшой интенсивности, которая может быть описана уравнением Кортевега – де Вриза – Бюргерса [16; 1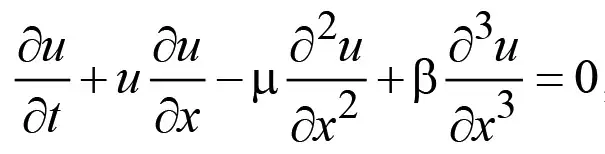7]

, (7)

где u – скорость течения газовоздушной смеси, представляющая собой искомую функцию u = u(x, t); μ – параметр, характеризующий вязкие свойства газа. Особенность уравнения (7) состоит в том, что оно обладает некоторой универсальностью, поскольку учитывает как диспергирующие свойства, характеризуемые параметром β, так и вязкие свойства газа, характеризуемые параметром вязкости μ.

Если вязкими свойствами газа, вызывающими диссипацию энергии, можно пренебречь, полагая параметр вязкости μ¦0, то уравнение (7) превращается в уравнение Кортевега – де Вриза, в котором учитываются только дисперсионные свойства газа. Если же параметр дисперсии газа β¦0, то уравнение (7) вырождается в уравнение Бюргерса, в котором учитываются только вязкие свойства газа. И, наконец, если μ¦0, β¦0, то уравнение (7) будет описывать одномерное течение идеального газа.

Из анализа уравнения (7) следует, что ввиду наличия слагаемого u·дu/дx оно нелинейное. Кроме этого, уравнение (7) является нестационарным, поскольку искомая функция зависит также от времени t. Однако, если перейти к новой переменной X с помощью соотношения

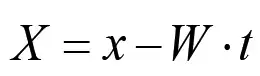, (8)

представляющего собой уравнение распространения волны, движущейся в положительном направлении оси x со скоростью W, то уравнение (7) преобразуется в обыкновенное дифференциальное уравнение 3-го порядка, которое удобно представить в следующем виде:

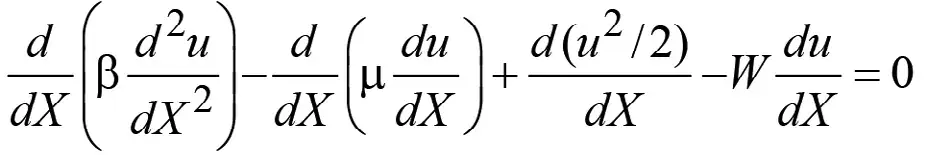. (9)

Интегрируя (9), при граничных условиях

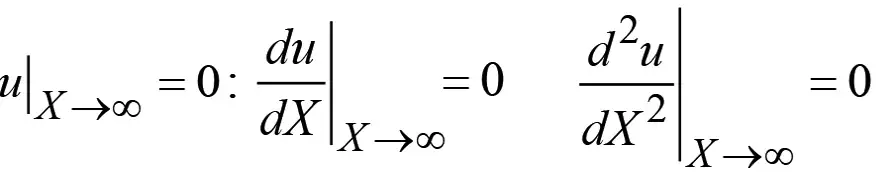
приходим к следующему нелинейному уравнению

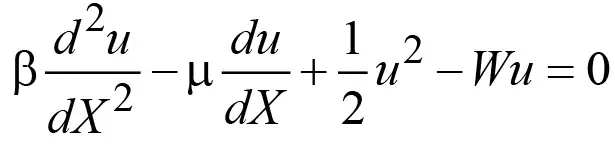, (10)

содержащему искомую функция в квадрате. Следовательно, найти его решение в замкнутом виде не представляется возможным. Поэтому мы предположим, что искомую функцию можно представить в виде суммы

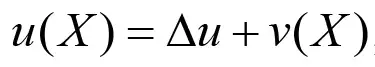, (11)

где v(X) – приращение скорости, представляющее собой малую величину, в силу чего имеет место соотношение 1 + v/Δu ≈ 1; Δu – разность скоростей на противоположных сторонах фронта волны, которую следует вычислять по формуле [16]

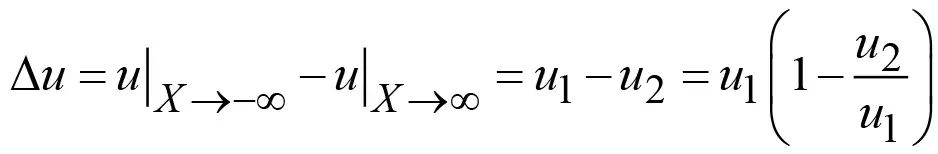, (12)

где u₁ – скорость газа при выбросе; u₂ – скорость течения воздуха в рудничной атмосфере. Поскольку u₂ << u₁, то 1 – u₂/u₁ ≈ 1 и тогда из формулы (12) вытекает Δu = u₁. Скорость фронта волны W в газовоздушной смеси можно рассматривать как полусумму скоростей на противоположных сторонах фронта волны [16]

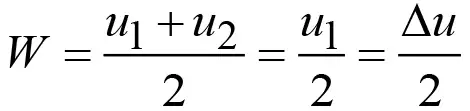. (13)

Подставив (11) в уравнение (10) и выполнив в полученном уравнении преобразования с учетом формулы (13), получим уравнение

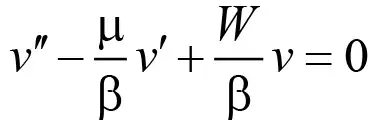, (14)

в котором штрихами обозначены производные по переменной X.

Решение уравнения (14) зависит от знака величины ψ

.

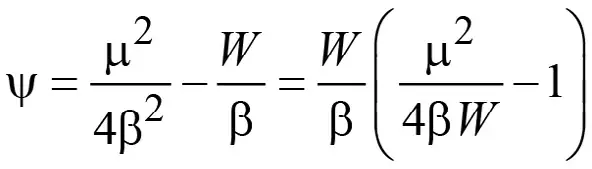Поскольку параметры вязкости и дисперсности газовоздушных смесей составляют величины порядка μ ~ 10–4 м²/с, β ~ 10–3 м³/с, а скорость фронта волны W ~ 50 м/с, то в рассматриваемом случае величиной μ2/(4βW) можно пренебречь по сравнению с единицей и поэтому ψ

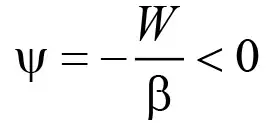
и тогда решение уравнения (14) представляется в виде [18]

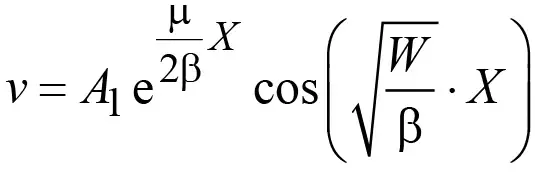. (15)

Для определения постоянной интегрирования A1 учтем, что v – малая величина, которая по условиям задачи в начале координат составляет

,

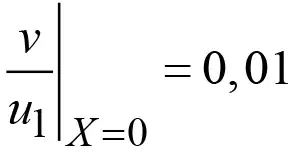и тогда из формулы (15) находим

.

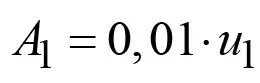Подставляя найденную величину A₁ сначала в формулу (15), а затем в (11) и учитывая, что Δu ≈ u₁, видим, что искомая функция

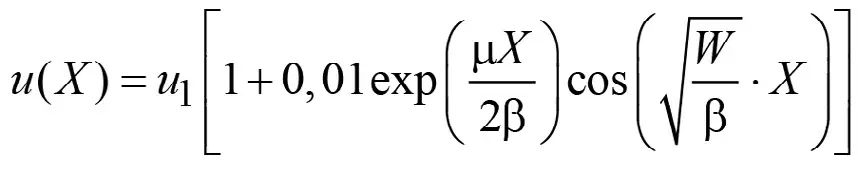, (16)

представляет собой совокупность экспоненциальной и тригонометрической функций.

Анализ полученных результатов

На базе представленных в статье формул выполнены вычислительные процедуры при условии, что выбрасываемый газ является метаном, имеющим следующие параметры: = 0,71 к г/м³; η = ζ = 12,3·10^–5 Па·с; cp = 1,82 кДж/ (кг·град); cv = 1,27 кДж/(кг·град).

Вычислительные процедуры начинаем с определения параметра вязкости μ, который найдем по формуле [19]

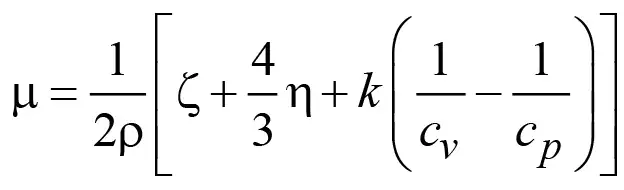, (17)

где η, ζ – коэффициенты вязкости смеси; c_v, c_p – удельные теплоемкости; k = c_p/c_v = 1,43 –показатель адиабаты Пуассона. Подставив данные в (17), находим μ = 4,44·10–4 м²/с. Далее вычислим параметр дисперсности μ, используя формулу (6), из которой находим

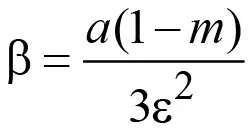(18)

где коэффициент m = a_gr/a, принятый в статье, равен 0,925. Пусть при внезапном выбросе газа зафиксирована его начальная скорость u₁ = 120 м/с и частота колебаний v = 350 Гц. Тогда мы можем вычислить скорость фронта волны W = u₁/2 = 60 м/с, ее длину λ = u₁/ v = 0,343 м, а затем по формуле (2) найдем волновое число ε = 2π/λ = 18,318 м^–1. Подставив полученные значения в формулу (18) и учитывая, что величина a в формуле (18) равна скорости u₁ выбрасываемого газа, найдем β = 4,47·10^–3 м³/с.

Подставляя в формулу (16) исходные и вычисленные данные, находим значения искомой функции u(X) при различных параметрах вязкости μ и дисперсности β газовоздушной смеси, а затем строим ее графики (рис. 1, 2).

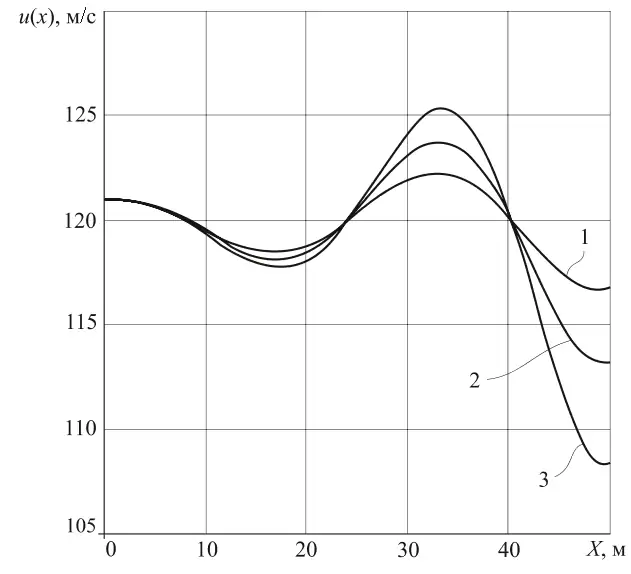 Рис. 1 Зависимость скорости газовоздушной смеси, сформированной внезапным выбросом газа, от параметра X при β = 8,95·10–3 м3/с и различных значений параметра вязкости μ

Fig. 1 Dependence of the velocity of the gas-air mixture formed by a sudden gas outburst on the parameter X at β = 8.95·10–3 m3/s and different values of the μ viscosity parameter

На рис. 1 показаны три графика функции u(X), где график 1 построен при значении μ = 4,44·10–4 м2/с, а графики 2 и 3 – соответственно при μ = 7,12·10–4 м2/с, μ = 9,04·10–4 м2/с. Все три графика качественно схожи и представляют собой периодические функции, амплитудные значения которых нарастают с ростом переменной X. Причем большим значениям параметра вязкости μ соответствуют большие значения функции u(X).

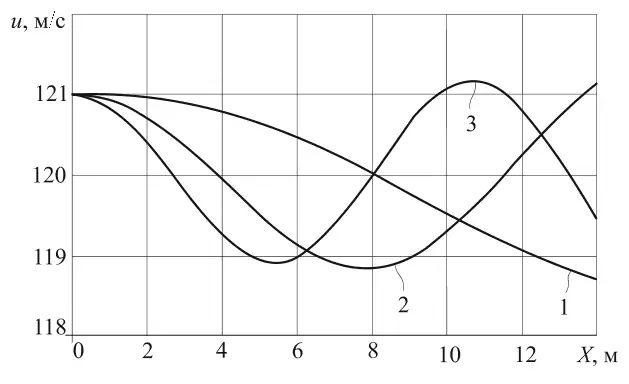Рис. 2 Зависимость скорости газовоздушной смеси, сформированной внезапным выбросом газа, от параметра X при μ = 4,44·10–4 м2/с и различных значений параметра дисперсности β

Fig. 2 Dependence of the velocity of the gas-air mixture formed by a sudden gas outburst on the parameter X at μ = 4.44·10–4 m2/s and different values of the β dispersion parameter

Графики функции u(X), представленные на рис. 2,

построены при μ = 4,44·10^–4 м²/с и различных значениях параметра дисперсности. График 1 построен при μ = 8,95·10–3 м³/с, график 2 – при β = 10,44·10^–3 м³/с, а график 3 – при β = 12,78·10^–3 м³/с.

Графики на рис. 2 также имеют отчетливый периодический характер, но по сравнению с графиками на предыдущем рисунке рост амплитудных значений с увеличением параметра X проявляется в меньшей степени. Более существенное отличие графиков на рис. 2 заключается в том, что их периоды различны и уменьшаются с ростом параметра дисперсности β.

К сказанному добавим еще два фрагмента:

1) если параметр вязкости изменяется, а параметр дисперсности – нет, то период функции u(X) также не меняется. Если же при постоянном значении параметра вязкости изменяется параметр дисперсности, то существенно изменяется и период функции u(X), причем тем существеннее, чем больше параметр дисперсности;

2) при увеличении аргумента функции u(X) рост амплитудных значений в большей степени проявляется при увеличении параметра вязкости, чем параметра дисперсности.

Заключение

Основные результаты исследований, приведенных в статье, заключаются в следующем:

– рассмотрено одномерное нестационарное течение газовоздушной смеси, описываемое нелинейным уравнением в частных производных 3-го порядка, в котором учтены вязкие и дисперсионные свойства смеси;

– обоснована формула, позволяющая вычислить скорость газовоздушной смеси в рудничной атмосфере в результате внезапного выброса метана при условии, что параметр вязкости смеси намного меньше его критического значения;

– в результате выполненных вычислительных процедур построен ряд графиков искомой функции u(X), характеризующих скорость газовоздушной смеси, анализ которых показал:

– период искомой функции u(X)не изменяется, если не изменяется параметр ее дисперсности;

– при увеличении аргумента искомой функции u(X) рост амплитудных значений в большей степени зависит от увеличения параметра вязкости, чем параметра дисперсности.

Список литературы

1. Христианович С.А. О волне выброса. Известия АН СССР. 1953;(12):1679–1688. Khristianovich S.A. On the emission wave. Izvestiya of the USSR Academy of Sciences. 1953;(12):1679–1688. (In Russ.)

2. Ходот В.В. Внезапные выбросы угля и газа. М.: Госгортехиздат; 1961. 363 с.

3. Трофимов В.А. Внезапный выброс угля и газа. Вынос угля и газа в выработанное пространство. Горный информационно-аналитический бюллетень. 2011;(S1):391‒405. Trofimov V.A. Sudden release of coal and gas. Removal of coal and gas into the developed space. Mining Informational and Analytical Bulletin. 2011;(S1):391‒405. (In Russ.)

4. Черданцев Н.В. Об одном подходе к построению решения задачи о выбросе угля и метана из краевой части пласта. Прикладная математика и механика. 2023;87(1):81–111. https://doi.org/10.31857/S0032823523010058 Cherdantsev N.V. About one approach to the construction of a solution to the problem of coal and methane emissions from the marginal zone of the formation. Prikladnaya Matematika i Mekhanika. 2023;87(1):81–111. (In Russ.) https://doi.org/10.31857/S0032823523010058

5. Черданцев Н.В., Черданцев С.В., Ли Х.У., Филатов Ю.М., Шлапаков П.А., Лебедев К.С. Об одном подходе к описанию суфлярных выделений газа из резервуаров угольного массива в горные выработки. Безопасность труда в промышленности. 2017;(3):45–52. Cherdantsev N.V., Cherdantsev S.V., Lee H.U., Filatov Y.M., Shlapakov P.A., Lebedev K.S. On one approach to the description of souffle gas emissions from coal reservoirs into mine workings. Occupational Safety in Industry. 2017;(3):45–52. (In Russ.)

6. Голубятников А.Н., Украинский Д.В. О точных аналитических решениях уравнений газовой динамики. Известия Российской академии наук. Механика жидкости и газа. 2020;(3):141‒150. https://doi.org/10.31857/S0568528120030044 Golubyatnikov A.N., Ukrainskii D.V. On exact analytical solutions of gas dynamic equations. Fluid Dynamics. 2020;55(3):423– 432. https://doi.org/10.1134/S0015462820030040

7. Голубкина И.В., Осипцов А.Н. Волны уплотнения с частичной и полной дисперсией в газокапельной среде с фазовыми переходами. Известия Российской академии наук. Механика жидкости и газа. 2022;(3):44‒55. Golubkina I.V., Osiptsov A.N. Partly and fully dispersed compression waves in a gas-droplet mixture with phase transitions. Fluid Dynamics. 2022;57(3):261–272. https://doi.org/10.1134/S0015462822030065

8. Булатов В.В., Владимиров И.Ю. Внутренние гравитационные волны от осциллирующего источника возмущений в стратифицированной среде с двухмерными сдвиговыми течениями. Известия Российской академии наук. Механика жидкости и газа. 2022;(4):60‒68. https://doi.org/10.31857/S0568528122040016 Bulatov V.V., Vladimirov I.Yu. Internal gravity waves generated by an oscillating disturbance source in a stratified medium in the presence of two-dimensional shear flows. Fluid Dynamics. 2022;57(4):477–485. https://doi.org/10.1134/s0015462822040012

9. Голубев А.Ю., Потокин Г.А. Пульсации давления на поверхности трехмерных обтекаемых выступающих тел. Известия Российской академии наук. Механика жидкости и газа. 2020;(1):57–63. https://doi.org/10.31857/S0568528120010065 Golubev A.Yu., Potokin G.A. Pressure fluctuations on the surfaces of three-dimensional protruding bodies in a gas flow. Fluid Dynamics. 2020;55(1):55–61. https://doi.org/10.1134/S0015462820010061

10. Sizykh G.B. Integral invariant of ideal gas flows behind a detached bow shock. Fluid Dynamics. 2021;56(8):1027–1030. https://doi.org/10.1134/S0015462821080097

11. Шевелев Ю.Д. Примеры установившихся осесимметричных течений идеальной несжимаемой жидкости. Известия Российской академии наук. Механика жидкости и газа. 2022;(2):3–13. https://doi.org/10.31857/S0568528122020074 Shevelev Yu.D. Examples of steady axisymmetric flows of an ideal incompressible fluid. Fluid Dynamics. 2022;57(2):111– 121. https://doi.org/10.1134/S0015462822020070

12. Gubaidullin D.A., Tukmakov D.A. Numerical study of the effect of polydispersity on the mass transfer of the dispersed phase during the passage of a shock wave through a gas suspension. Fluid Dynamics. 2023;58(7):1373–1383. https://doi.org/10.1134/S0015462823601997

13. Островский Л.А., Потапов А.И. Введение в теорию модулированных волн. М.: Физматлит; 2003. 400 с.

14. Черданцев С.В., Шлапаков П.А., Голоскоков С.И., Ерастов А.Ю., Лебедев К.С., Шлапаков Е.А. О формировании напряженного состояния в шахтной перемычке при прохождении через нее ударной волны. Вестник Научного центра ВостНИИ по промышленной и экологической безопасности. 2023;(1):47–62. https://doi.org/10.25558/VOSTNII.2023.40.18.005 Cherdantsev S.V., Shlapakov P.A., Goloskokov S.I., Erastov A.Yu., Lebedev K.S., Shlapakov E.A. On formation of stress state in shaft bridge when shock wave passes through it. Bulletin of Scientific Centre VostNII for Industrial and Environmental Safety. 2023;(1):47–62. (In Russ.) https://doi.org/10.25558/VOSTNII.2023.40.18.005

15. Черданцев С.В., Шлапаков П.А., Ерастов А.Ю., Лебедев К.С. Напряженное состояние в шахтной перемычке, обусловленное давлением на фронте ударной волны. Безопасность труда в промышленности. 2023;(2):7–14. https://doi.org/10.24000/0409-2961-2023-2-7-14 Cherdantsev S.V., Shlapakov P.A., Erastov A.Yu., Lebedev K.S. Stress state in a shaft jumper due to pressure at the shock wave front. Occupational Safety in Industry. 2023;(2):7–14. (In Russ.) https://doi.org/10.24000/0409-2961-2023-2-7-14

16. Карпман В.И. Нелинейные волны в диспергирующих средах. М.: Наука; 1973. 176 с.

17. Уизем Дж. Линейные и нелинейные волны. М.: Мир; 1977. 622 с.

18. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Наука; 1974. 331 с.

19. стон Т., Стюарт И. Теория катастроф и ее приложения. М.: Физматлит; 1980. 608 с.