Развитие подходов к расчету параметров напряженно-деформированного состояния массива пород по результатам измерений деформаций на торце скважины
 И.Э. Семенова1, П.В. Амосов2, Н.Н. Кузнецов1, В.А. Некрасов1
И.Э. Семенова1, П.В. Амосов2, Н.Н. Кузнецов1, В.А. Некрасов1
1 Горный институт Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация
2 Институт проблем промышленной экологии Севера Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация
Горная Промышленность №5S / 2024 стр.122-129
Резюме: Для обеспечения безопасных условий отработки месторождений полезных ископаемых необходимой является информация о напряженно-деформированном состоянии массивов горных пород. Существует ряд методов, позволяющих получить подобного рода информацию. Один из них, нашедший широкое применение на горных предприятиях, заключается в использовании характеристики упругого восстановления формы и размеров элемента породного массива при искусственном нарушении его связи с основным массивом (метод полной разгрузки в варианте торцевых измерений). Для его корректной реализации требуется математический аппарат, позволяющий перейти от напряжений на забое скважины к напряжениям в массиве пород без использования эмпирических коэффициентов. В работе представлены результаты разработки математического аппарата для расчета напряжений, действующих в массиве пород и определяемых на основании метода разгрузки в варианте торцевых измерений. Показана возможность использования полученных в ходе многолетних натурных и лабораторных исследований эмпирических коэффициентов (коэффициент концентрации и коэффициент влияния осевого напряжения) для перехода от напряжений на торце скважины (плоское напряжённое состояние) к напряжениям в массиве (объемное напряжённое состояние). Предложен подход для расчета компонент тензора напряжений в плоскости забоя трех взаимно перпендикулярных скважин через величины деформаций четырехдатчиковой розетки. Приведен подход для перехода от направлений и величин напряжений на плоскости замеров к направлению и величине главных напряжений в массиве.
Ключевые слова: напряженно-деформированное состояние, измерение напряжений, тензор напряжений, метод полной разгрузки на торце скважины, теория упругости, массив горных пород, скважина
Для цитирования: Семенова И.Э., Амосов П.В., Кузнецов Н.Н., Некрасов В.А. Развитие подходов к расчету параметров напряженно-деформированного состояния массива пород по результатам измерений деформаций на торце скважины. Горная промышленность. 2024;(5S):122–129. https://doi.org/10.30686/1609-9192-2024-5S-122-129
Информация о статье
Поступила в редакцию: 10.08.2024
Поступила после рецензирования: 02.10.2024
Принята к публикации: 11.10.2024
Информация об авторах
Семенова Инна Эриковна – кандидат технических наук, руководитель отдела геомеханики, Горный институт Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Амосов Павел Васильевич – кандидат технических наук, ведущий научный сотрудник лаборатории междисциплинарных эколого-экономических исследований, Институт проблем промышленной экологии Севера Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Кузнецов Николай Николаевич – кандидат технических наук, руководитель лаборатории инструментальных исследований состояния горных пород Арктической зоны РФ, отдел геомеханики, Горный институт Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Некрасов Валерий Аркадьевич – ведущий инженер лаборатории инструментальных исследований состояния горных пород Арктической зоны РФ, отдел геомеханики, Горный институт Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Введение
Геомеханическое обоснование и сопровождение горных работ в последние десятилетия стали необходимыми условиями обеспечения эффективности и безопасности отработки месторождений, как в России, так и в мире [1–3].
При этом важными составляющими являются: исследования напряженно-деформированного состояния (НДС) и физико-механических свойств горных пород; мониторинг геомеханического и геодинамического состояния массива горных пород на различных масштабных уровнях при активном техногенном воздействии; разработка мероприятий для снижения рисков; прогноз геомеханической ситуации (в том числе с использованием численных методов).
Информация о поле напряжений участков земной коры является одной из ключевых для перечисленных направлений на всех этапах ведения горных работ – от выбора системы разработки и ее параметров до прогноза трансформации полей напряжений в процессе выемки полезного ископаемого и принятия решений по обеспечению геодинамической безопасности горных работ.
Существует ряд прямых и косвенных методов для качественной и количественной оценки действующих напряжений в массиве горных пород. Натурные методы оценки параметров НДС можно условно разделить на три группы — скважинные методы; методы, основанные на исследовании образцов керна; методы контроля напряжений на обнажениях горных пород. Наиболее широкое применение на горных предприятиях получили два скважинных метода: метод полной разгрузки [4–6] и метод гидроразрыва [6–9].
Принцип, лежащий в основе метода полной разгрузки для определения напряжений в массиве горных пород, изложен в ряде работ [10–19]. Сопутствующая методу информация, касающаяся способов и средств определения полей деформаций и напряжений, представлена в публикациях [20–23]. Указанный метод основан на использовании характеристики упругого восстановления формы и размеров элемента породного массива при искусственном нарушении его связи с основным массивом. На основании измеренных деформаций упругого восстановления торца скважины при выбуривании керна можно определить как величину, так и направление главных напряжений нетронутого массива. Для этого бурится не менее трех разноориентированных взаимно ортогональных скважин длины, достаточной для обеспечения расположения датчиков в зоне, не подверженной влиянию от проходки горных выработок. На забой скважины специальным образом размещают розетку с тензодатчиками. Затем производят обуривание скважины, при котором элемент породного массива освобождается от действующих в нем напряжений и испытывает деформации, фиксируемые датчиками.
Далее применяют формулы теории упругости, связывающие измеренные деформации и соответствующие им напряжения: на 1-м шаге определяют главные напряжения в плоскости торца скважины, а на 2-м по определенным напряжениям на трех взаимно перпендикулярных скважинах определяют поле напряжений на рассматриваемом участке массива пород.
Исследование напряженного состояния массивов горных пород с использованием метода разгрузки в варианте торцевых измерений выполняется сотрудниками ГоИ КНЦ РАН на протяжении 60 лет. За это время разработано и модифицировано необходимое оборудование для измерения деформаций в массиве, а также проработаны и обоснованы методы аналитической обработки полученных результатов [24; 25]. В качестве «тонкого места» используемого Горным институтом аналитического подхода можно отметить применение экспериментально установленных коэффициентов для перехода от напряжений, рассчитанных на забое скважины, к напряжениям в массиве пород. Значения таких коэффициентов зависят от определяемых на образцах значений коэффициента Пуассона, вариация которых для одного типа пород может составлять порядка 20‒30%. Это, в свою очередь, может вносить дополнительную погрешность в окончательные результаты рассчитываемых значений напряжений.
В связи с этим целью работы является создание математического аппарата для обоснованного перехода от напряжений на забое скважины к напряжениям в массиве пород без использования эмпирических коэффициентов, что, в итоге, позволит увеличить точность и надежность получаемых результатов.
Результаты и их обсуждение
Расчет напряжений в массиве пород по схеме Горного института КНЦ РАН
Для измерения деформаций в массиве пород Горным институтом КНЦ РАН использовалась четырехэлементная розетка (рис. 1) с датчиками, расположенными под углами β1, β2, β3 и β4 равными 0, 60, 120 и 90° соответственно [24; 25].
![Рис. 1 Схема расположения тензодатчиков на розетке по [24] Fig. 1 Layout of the strain gauges on the socket according to [24]](/images/2024/05S_2024/122_1.webp) Рис. 1 Схема расположения тензодатчиков на розетке по [24]
Рис. 1 Схема расположения тензодатчиков на розетке по [24]
Fig. 1 Layout of the strain gauges on the socket according to [24]
На основании измеренных в ходе разгрузки значений деформаций выполняли переход к напряжениям на забое скважины (плоское напряженное состояние) с использованием формул теории упругости (1–4):
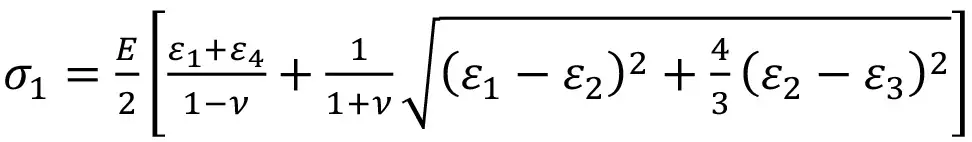 (1)
(1)
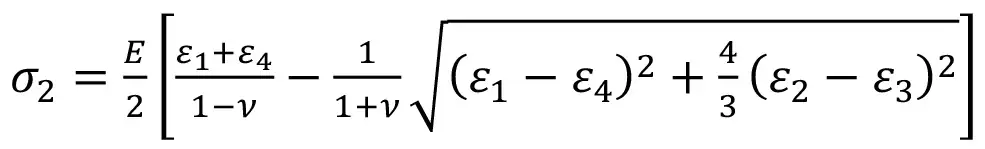 (2)
(2)
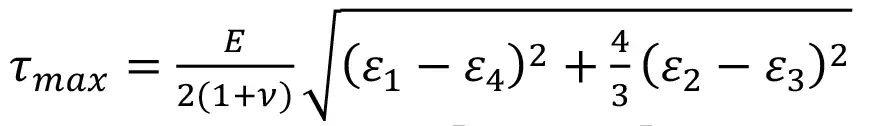 (3)
(3)
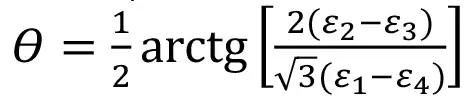 (4)
(4)
где σ1, σ2, τmax ‒ главные нормальные и максимальное касательное напряжения, МПа; E ‒ модуль упругости, МПа; ν ‒ коэффициент Пуассона, ε1, ε2, ε3, ε4 ‒ относительные деформации, измеренные с использованием соответствующих тензодатчиков; θ ‒ угол наклона главных напряжений. Экспериментально установлено [24], что в условиях плоского напряженного состояния, которое обусловлено действием боковых напряжений, главные напряжения, рассчитанные с использованием формул (1–2), оказываются больше по величине боковых напряжений, действующих вдалеке от скважины (в массиве пород). В связи с этим введен коэффициент увеличения боковых напряжений – коэффициент концентрации K1.
В лабораторных условиях на объемных моделях определено, что значение коэффициента концентрации непостоянно и зависит от значения коэффициента Пуассона [24]. На рис. 2 представлен график зависимости изменения значений коэффициента концентрации от значения коэффициента Пуассона. Приводимая зависимость является справедливой как для нормальных, так и для касательных напряжений.
![Рис. 2 Зависимость коэффициента концентрации (K1) от коэффициента Пуассона (ν) по [24] Fig. 2 Dependence of the concentration coefficient (K1) on the Poisson's ratio (ν) according to [24]](/images/2024/05S_2024/122_2.webp) Рис. 2 Зависимость коэффициента концентрации (K1) от коэффициента Пуассона (ν) по [24]
Рис. 2 Зависимость коэффициента концентрации (K1) от коэффициента Пуассона (ν) по [24]
Fig. 2 Dependence of the concentration coefficient (K1) on the Poisson's ratio (ν) according to [24]
В случае, когда действует только одно осевое напряжение, забой скважины будет деформироваться так, как если бы действовали только два боковых напряжения. Главные напряжения, вычисленные в этом случае, будут равны между собой, противоположны по знаку осевому напряжению и меньше его по абсолютной величине. В связи с этим, отношение боковых напряжений, вызванных действием осевого напряжения, к осевому напряжению обозначили как коэффициент влияния осевого напряжения K2 [24].
Экспериментально установлено [24], что значения коэффициента влияния осевого напряжения также в основном зависят от значений коэффициента Пуассона. График зависимости между этими двумя параметрами представлен на рис. 3.
![Рис. 3 Зависимость коэффициента влияния осевого напряжения (K2) от коэффициента Пуассона (ν) по [24] Fig. 3 Dependence of the axial stress influence coefficient (K2) on the Poisson’s ratio (ν) according to [24]](/images/2024/05S_2024/122_3.webp) Рис. 3 Зависимость коэффициента влияния осевого напряжения (K2) от коэффициента Пуассона (ν) по [24]
Рис. 3 Зависимость коэффициента влияния осевого напряжения (K2) от коэффициента Пуассона (ν) по [24]
Fig. 3 Dependence of the axial stress influence coefficient (K2) on the Poisson’s ratio (ν) according to [24]
После определения коэффициентов концентрации и влияния осевых напряжений переходят к расчету фактических значений напряжений, действующих в массиве пород до бурения скважины (плоское напряженное состояние) по следующим формулам [24]:
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
где σf1, σf2, τfmax ‒ главные напряжения, существовавшие в точке измерения до образования скважины, ‒ угол наклона главных напряжений.
Фактические главные напряжения в массиве горных пород в условиях трехосного напряженного состояния находят из следующих выражений:
для скважины №1:
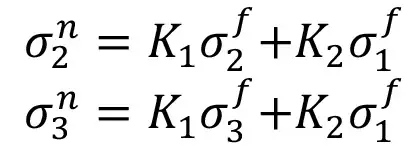
для скважины №2:
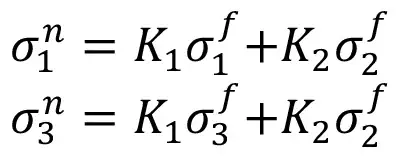
для скважины №3:
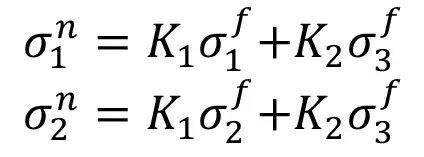
Следует отметить, что указанные выше уравнения справедливы при измерениях напряжений в массиве пород, выполняемых в трех взаимно ортогональных скважинах, ориентированных в направлении действия главных напряжений.
Расчет напряжений на забое скважины и в массиве пород без использования дополнительных эмпирических коэффициентов
Для перехода от расчета напряжений на торце скважины к расчету напряжений в массиве пород без использования дополнительных эмпирических коэффициентов (коэффициент концентрации и коэффициент влияния осевого напряжения) воспользуемся аналитическими подходами, представленными в работах E.R. Leeman [10], Кобаяси [21], а также в учебно-методических пособиях [26–29].
Введем обозначения датчиков: символы A, B, C, D соответствуют углам наклона к оси X (углы βA, βB, βC и βD равными 0, 45, 90 и 135° соответственно). Отметим, что в работе E.R. Leeman [10] рассматривается ситуация для трех датчиков с углами расположения 0°, 90° и 225°.
Зафиксируем принятую систему координат X0Y (ось Z направлена на нас): ось Х совпадает с направлением датчика А, ось Y с направлением датчика С (рис. 4). В условиях плоского напряженного состояния величины σxx, σyy и τxy отличны от нуля, причем направления главных напряжений неизвестны. На свободной поверхности остальные компоненты тензора напряжений равны нулю.
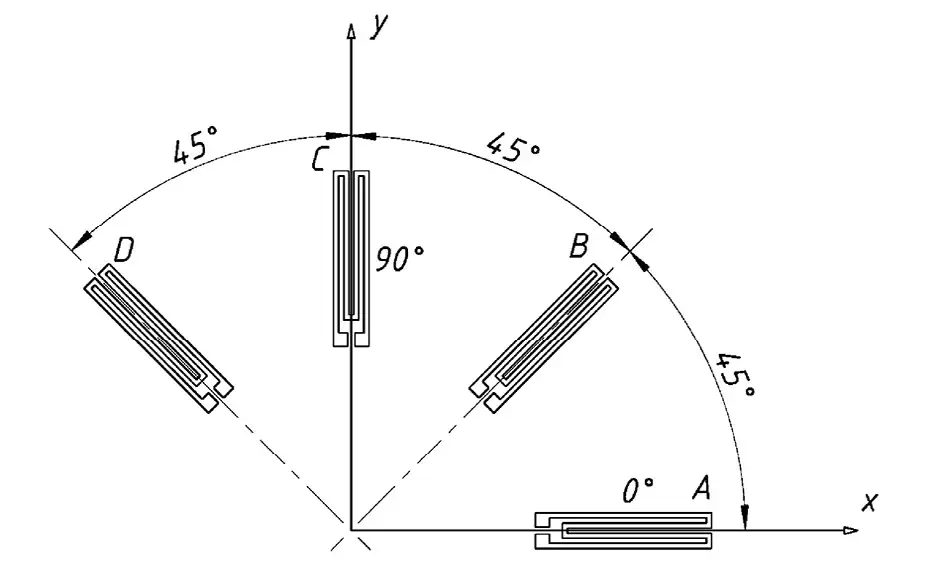 Рис. 4 Схема расположения тензодатчиков на розетке
Рис. 4 Схема расположения тензодатчиков на розетке
Fig. 4 Layout of the strain gauges on the socket
Для преобразования измеренных деформаций, возникающих в площадках, перпендикулярных к свободной поверхности, необходимо знать деформации в трех направлениях на свободной поверхности, а также упругие постоянные материала E (модуль упругости породы) и ν (коэффициент Пуассона).
Ищем три неизвестных параметра, определение которых позволяет полностью описать напряженное состояние в заданной точке. Эти неизвестные параметры – главные напряжения σ1 и σ2 и угол β1 наклона главного напряжения к оси X.
![Рис. 5 Три тензодатчика, ориентированные под произвольными углами относительно оси X (по А. Кобаяси [21]) Fig. 5 Three strain gauges oriented at arbitrary angles with respect to the X axis (according to A. Kobayashi [21])](/images/2024/05S_2024/122_5.webp) Рис. 5 Три тензодатчика, ориентированные под произвольными углами относительно оси X (по А. Кобаяси [21])
Рис. 5 Три тензодатчика, ориентированные под произвольными углами относительно оси X (по А. Кобаяси [21])
Fig. 5 Three strain gauges oriented at arbitrary angles with respect to the X axis (according to A. Kobayashi [21])
В монографии Кобаяси [21] в общем случае рассмотрено три тензодатчика, установленные вдоль осей А, В и С (рис. 5). На текущем шаге будем придерживаться терминологии указанной монографии. Уравнения преобразования деформаций при повороте осей координат имеют вид:
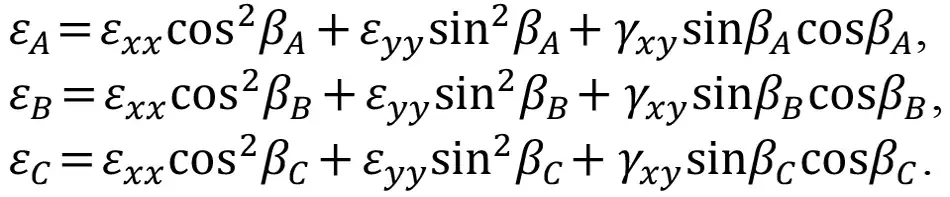 (9)
(9)
По заданным углам βA, βB, βC и известным по результатам измерений деформаций εA, εB, εC компоненты тензора деформаций в декартовой системе координат (εxx, εyy и τxy) находятся путем решения системы уравнений (9). Главные деформации ε1 и ε2, а также их направления вычисляются по формулам:
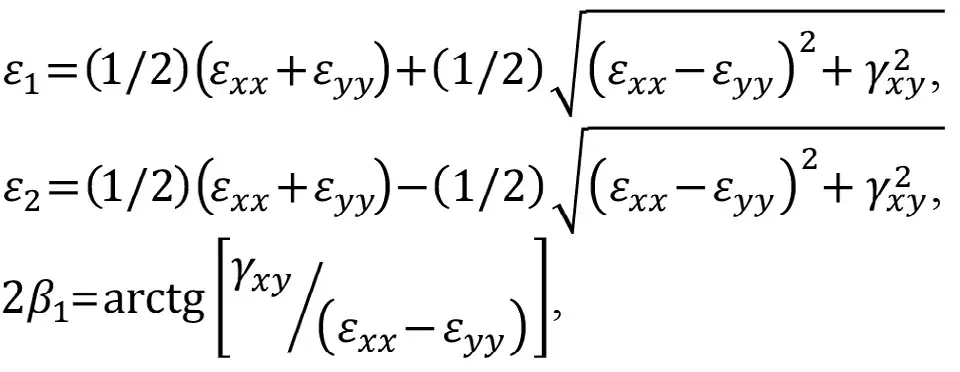 (10)
(10)
где β1 – угол наклона деформации ε1 к оси X. В отношении угла β1 А. Кобаяси [21] обращает внимание, что на самом деле имеем два значения. Одно значение дает угол β1 между ε1 и осью X, а другое – угол β2 между осью ε2 и осью X.
Область изменения угла β1 может быть определена из конкретных условий размещения датчиков.
Для нашей четырехэлементной прямоугольной розетки с описанными выше углами размещения датчиков имеем:
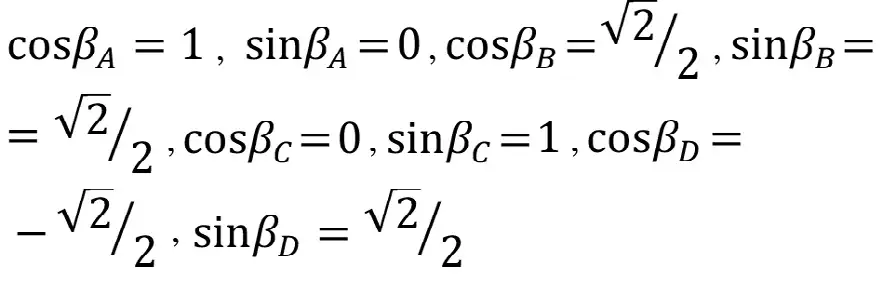
Система уравнений (9) в нашем случае имеет вид:
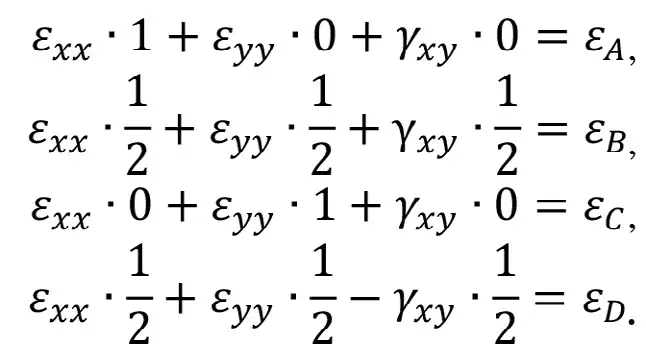
Из первых 3-х уравнений имеем очевидные решения:
![]()
Если сложить 2-е и 4-е уравнения, то с учетом приведенных решений получим:
![]()
т.е. 3-ю компоненту деформаций можно записать в форме:
![]()
Таким образом, задействовали все 4 измеряемые деформации.
Используя уравнения (10), по известным компонентам тензора деформаций вычисляем главные деформации ε1 и ε2, а также их направления:
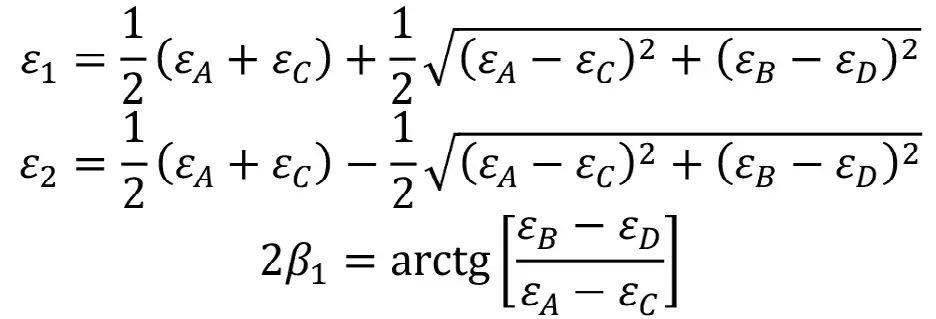
Упрощаем тригонометрические формулы в соответствии с E.R. Leeman [10]:
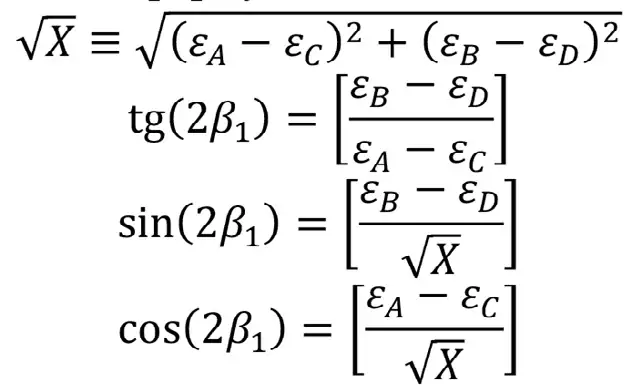
По известным главным деформациям ε1 и ε2 записываем главные напряжения σ1 и σ2 и максимальное тангенциальное τmax на торце скважины. Далее выражаем их через измеренные деформации:
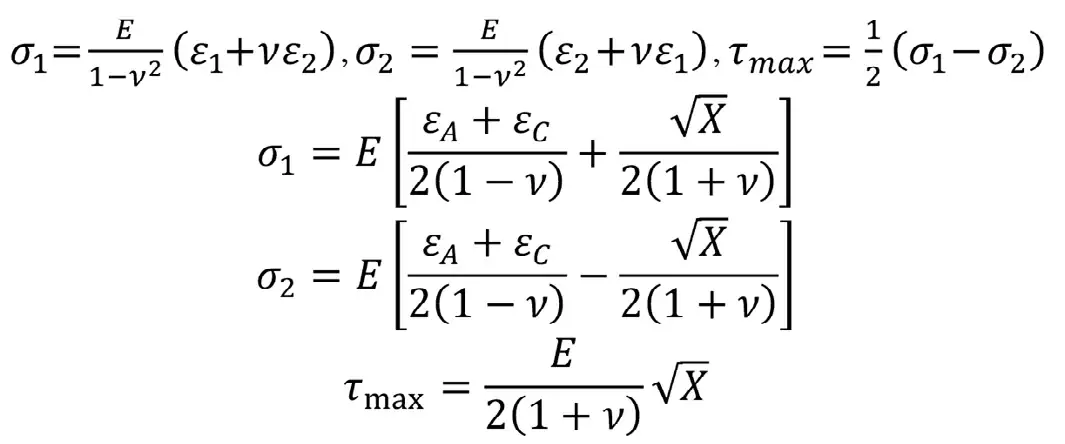
По известным главным напряжениям запишем компоненты напряжений по выбранным направлениям X и Y [26–29]:
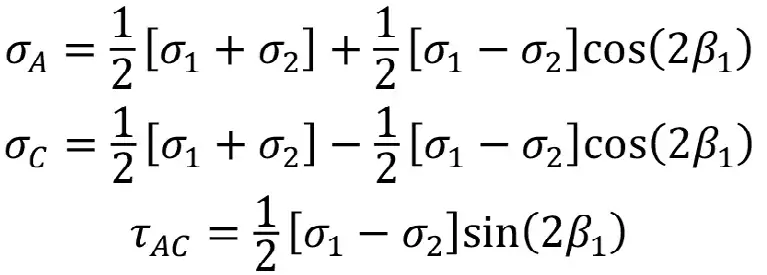
Выразим результат через измеренные деформации: Таким образом, компоненты тензора напряжений в плоскости поверхности лба забоя скважин (1, 2 и 3) через величины деформаций, полученные по четырем датчикам, будут определяться по следующим формулам:
для скважины №1 (ось скважины совпадает с осью Z)
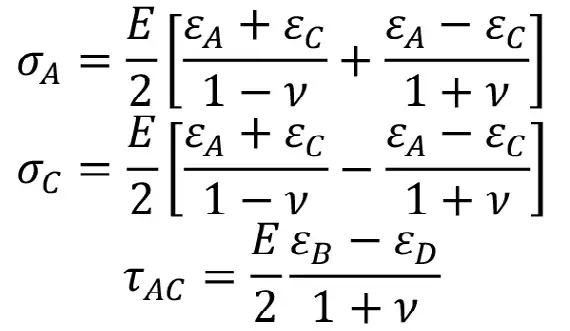
для скважины №2 (ось скважины совпадает с осью X)
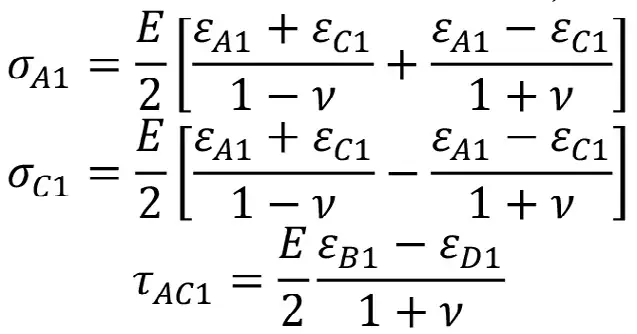
для скважины №3 (ось скважины совпадает с осью Y)
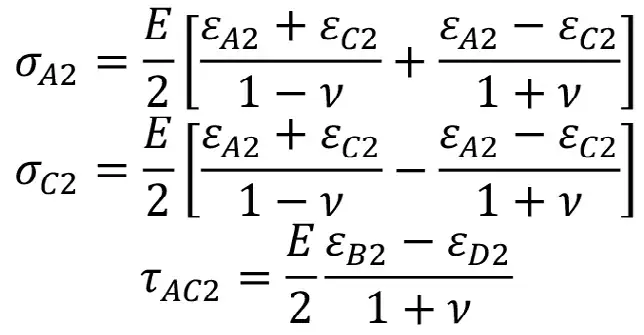
В правых частях уравнений для скважин №1–№3 фигурируют относительные деформации, полученные по соответствующему датчику деформаций.
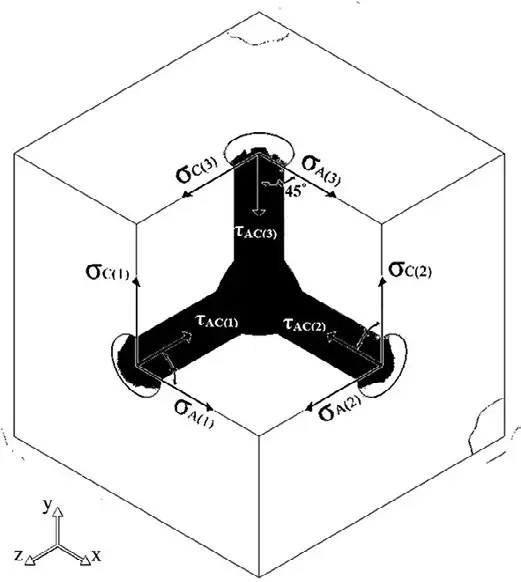 Рис. 6 Компоненты нормальных и касательных напряжений, рассчитываемых по результатам замеров в трех взаимно ортогональных скважинах
Рис. 6 Компоненты нормальных и касательных напряжений, рассчитываемых по результатам замеров в трех взаимно ортогональных скважинах
Fig. 6 Components of the normal and tangential stresses calculated based on the measurements in three mutually orthogonal boreholes
На основании полученных уравнений выполняют переход от напряжений, рассчитанных на забое скважин (рис. 6), к напряжениям, действующим в массиве пород.
Представим компоненты тензора напряжений σ'X, σ'Y, τ'XY, следуя E.R. Leeman [10], следующим образом (штрихи относятся к напряжениям в плоскости поверхности лба забоев, в нашем случае σA и σC соответствуют направлению осей X и Y):
![]()
![]()
где a, b, c и d – эмпирические коэффициенты, определяемые по табл. 1.
Таблица 1 Эмпирические коэффициенты для определения компонент тензора напряжений в массиве пород
Таблица 1 Empirical coefficients for determining components of the stress tensor in the rock mass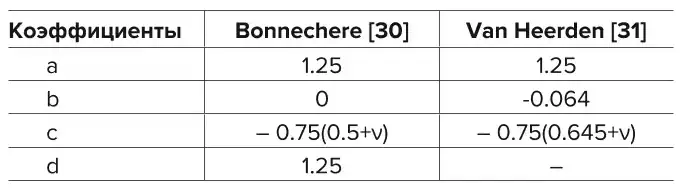
Запишем следующую систему уравнений, используя следующее правило: 1-я скважина последовательность XYZ; 2-я скважина последовательность YZX и 3-я скважина последовательность ZXY.
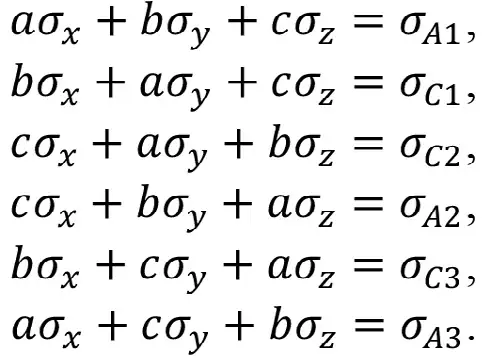
Система уравнений для вычисления нормальных компонент напряжений σx, σy и σz в породном массиве, составленная из уравнений для скважин №1–№2, имеет вид:
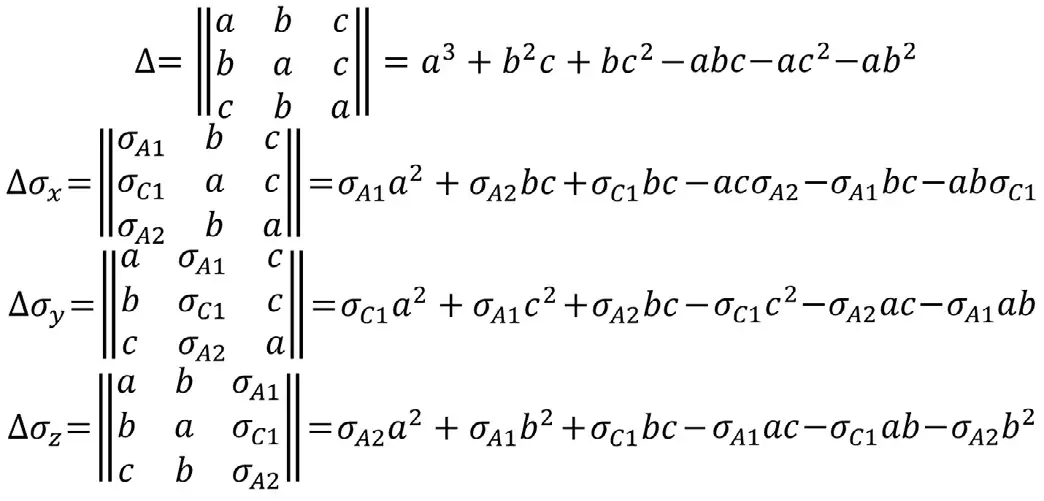
Последовательно вычисляем нормальные и касательные компоненты напряжений в породном массиве:
![]()
![]()
Запишем тензор компонент напряжений:
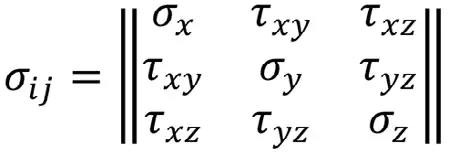
Переходим к задаче определения главных напряжений в массиве, которые можно найти из решения кубического уравнения:
![]()
Коэффициенты этого уравнения – инварианты тензора напряжений и вычисляются по формулам:
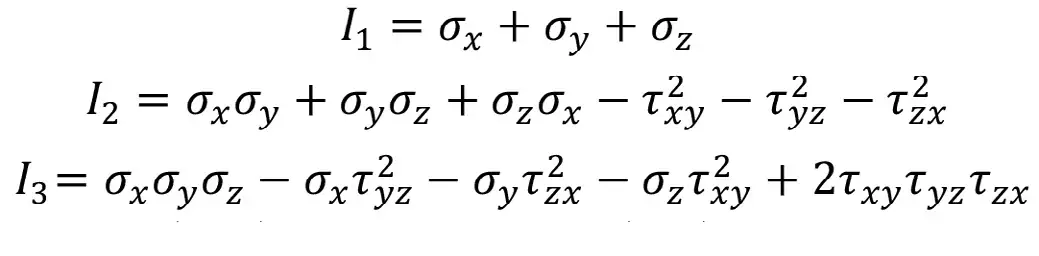
Находим максимальное (max) – минимальное (min) – промежуточное (med). Записываем тензор главных напряжений:
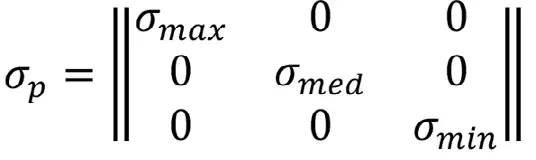
Затем находим углы наклона площадок главных напряжений, выраженных через направляющие косинусы:
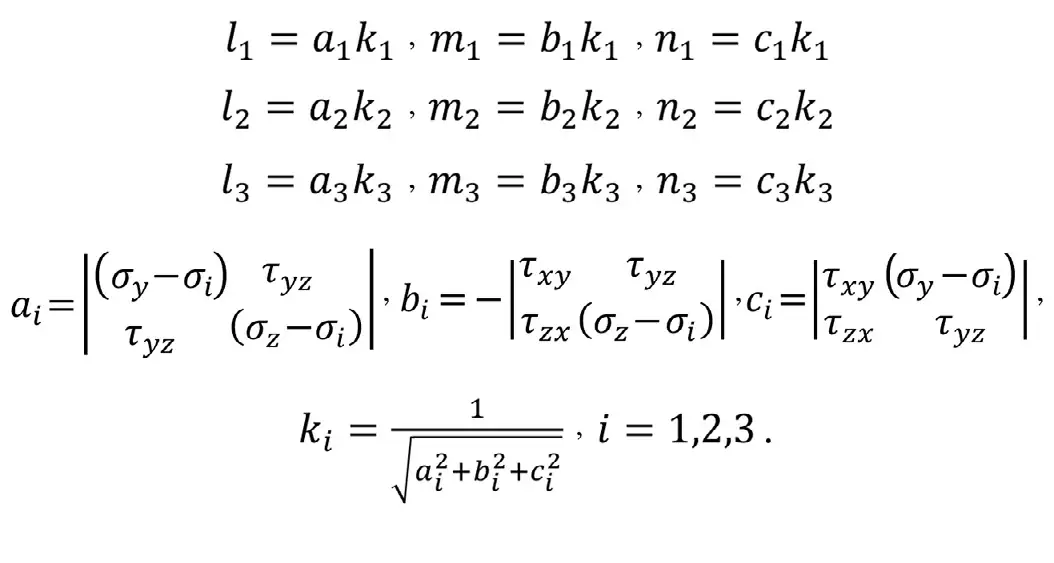
Углы поворота вектора, совпадающего с i-м главным напряжением σi, относительно принятой глобальной системы координат, определяются по следующим формулам:
![]()
Таким образом, находим искомые направляющие косинусы векторов:
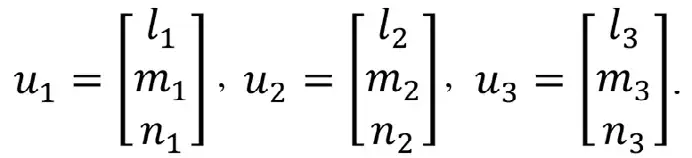
Заключение
Таким образом, в работе представлены результаты в части разработки математического аппарата для расчета напряжений, действующих в массиве пород и определяемых на основании метода разгрузки в варианте торцевых измерений. Показана возможность использования полученных в ходе многолетних натурных и лабораторных исследований эмпирических коэффициентов (коэффициент концентрации и коэффициент влияния осевого напряжения) для перехода от напряжений на торце скважины (плоское напряженное состояние) к напряжениям в массиве (объемное напряженное состояние).
С целью увеличения точности получаемых результатов и ухода от дополнительных эмпирических коэффициентов предложен подход для расчета компонент тензора напряжений в плоскости забоя трех взаимно перпендикулярных скважин через величины деформаций четырехдатчиковой розетки для схемы размещения тензодатчиков с углами равными 0, 45, 90 и 135°.
Описан подход, который включает в себя математические формулы и алгоритм перехода от направлений и величин напряжений на плоскости замеров к направлению и величине главных напряжений в массиве. Для вычисления нормальных компонент напряжений σx, σy и σz представлен один из возможных алгоритмов расчета напряжений в массиве.
Список литературы
1. Козырев А.А., Панин В.И., Семенова И.Э., Рыбин В.В. Геомеханическое обеспечение горных работ на горнодобывающих предприятиях Мурманской области. Горный журнал. 2019;(6):45–50. https://doi.org/10.17580/gzh.2019.06.05 Kozyrev A.A., Panin V.I., Semenova I.E., Rybin V.V. Geomechanical support of mining operations in mines of the Murmansk Region. Gornyi Zhurnal. 2019;(6):45–50. (In Russ.) https://doi.org/10.17580/gzh.2019.06.05
2. Maleki H., Lawson H. Analysis of geomechanical factors affecting rock bursts in sedimentary rock formations. Procedia Engineering. 2017;191:82–88.
3. Еременко А.А., Шапошник Ю.Н., Филиппов В.Н., Конурин А.И. Развитие научных основ безопасной и эффективной геотехнологии при освоении удароопасных месторождений Западной Сибири и Крайнего Севера. Горный журнал. 2019;(10):33–39. https://doi.org/10.17580/gzh.2019.10.03 Eremenko A.A., Shaposhnik Yu.N., Filippov V.N., Konurin A.I. Development of scientific framework for safe and efficient geotechnology for rockburst-hazardous mineral deposits in Western Siberia and the Far North. Gornyi Zhurnal. 2019;(10): 33–39. (In Russ.) https://doi.org/10.17580/gzh.2019.10.03
4. Турчанинов И.А. Сравнительные испытания прецизионной тензометрической шахтной аппаратуры. Уникальные приборы. 1972;(10):127–128. Turchaninov I.A. Comparative testing of precision strain gauge mine instrumentation. Unikalnye Pribory. 1972;(10):127–128. (In Russ.)
5. Herget G. Rock stress and rock stress monitoring in Canada. In: Hudson J.A. (ed.). Rock Testing and Site Characterization: Principles, Practice and Projects. Elsevier Ltd.; 1995, pp. 473–496. https://doi.org/10.1016/B978-0-08-042066-0.50026-4
6. Subrahmanyam D.S. Evaluation of hydraulic fracturing and overcoring methods to determine and compare the in situ stress parameters in porous rock mass. Geotechnical and Geological Engineering. 2019;37(6):4777–4787. https://doi.org/10.1007/s10706-019-00937-7
7. Hubbert M.K., Willis D.G. Mechanics of hydraulic fracturing. Transactions of the AIME. 1957;210(01):153–168. https://doi.org/10.2118/686-g
8. Курленя М.В. Развитие метода гидроразрыва для исследования напряженного состояния массива горных пород. Физико-технические проблемы разработки полезных ископаемых. 1994;(1):3–20. Kurlenya M.V., Leont’ev A.V., Popov S.N. Development of hydraulic fracturing for studying the stressed state of a rock mass. Journal of Mining Science. 1994;30(1):1–15. https://doi.org/10.1007/BF02048767
9. Леонтьев А.В., Рубцова Е.В., Леконцев Ю.М., Качальский В.Г. Измерительно-вычислительный комплекс «Гидроразрыв». Физико-технические проблемы разработки полезных ископаемых. 2010;(1):104–110. Leont’ev A.V., Rubtsova E.V., Lekontsev Yu.M., Kachal’sky V.G. Measuring-computing complex “Gidrorazryv”. Journal of Mining Science. 2010;46(1):89–94. https://doi.org/10.1007/s10913-010-0013-x
10. Leeman Е.R. The CSIR “doorstopper” and triaxial rock stress measuring instruments. Rock Mechanics. 1971;3(1):25–50. https://doi.org/10.1007/BF01243550
11. Borsetto M., Martinetti S., Ribacchi R. Interpretation of in situ stress measurements in anisotropic rocks with the doorstopper method. Rock Mechanics and Rock Engineering. 1984;17(3):167–182. https://doi.org/10.1007/BF01042548
12. Ljunggren C., Chang Y., Janson T., Christiansson R. An overview of rock stress measurement methods. International Journal of Rock Mechanics and Mining Sciences. 2003;40(7-8):975–989. https://doi.org/10.1016/j.ijrmms.2003.07.003
13. Siren T., Hakala M., Perras M.A.Reliable in situ rock stress measurement from the excavation surface. In: Hudyma M., Potvin Y. (eds). UMT 2017: Proceedings of the First International Conference on Underground Mining Technology. Australian Centre for Geomechanics, Perth; 2017, pp. 477–486. https://doi.org/10.36487/ACG_rep/1710_38_Perras
14. Guido S., Acerbis R., Sossi G. Practice of the Doorstopper stress measurement method during the last 30 years in Italy. IOP Conference Series: Earth and Environmental Science. 2021;833:012167. https://doi.org/10.1088/1755-1315/833/1/012167
15. Feng Y., Pan P.-Z., Wang Z., Liu X., Miao S. A novel indirect optical method for rock stress measurement using microdeformation field analysis. Journal of Rock Mechanics and Geotechnical Engineering. 2024;16(9):3616–3628. https://doi.org/10.1016/j.jrmge.2023.10.011
16. Мельников Д.Н. Измерение напряжений в массиве пород Ждановского месторождения методом разгрузки (торцевой вариант). Вестник Кольского научного центра РАН. 2019;(1):57–61. https://doi.org/10.25702/KSC.2307-5228.2019.11.1.57-61 Melnikov D.N. Stress measurements in rock mass of the Zhdanovskoe deposit by the doorstopper method. Herald of the Kola Science Centre of RAS. 2019;(1):57–61. (In Russ.) https://doi.org/10.25702/KSC.2307-5228.2019.11.1.57-61
17. Самсонов А.А. Оценка состояния массива горных пород удароопасного месторождения «Олений ручей» по результатам измерений напряжений. Вестник Кольского научного центра РАН. 2019;(1):62–67. https://doi.org/10.25702/KSC.2307-5228.2019.11.1.62-67 Samsonov A.A. Assessment of rock mass state of Oleniy ruchey rock burst deposit based on the results of stress measurements. Herald of the Kola Science Centre of RAS. 2019;(1):62–67. (In Russ.) https://doi.org/10.25702/KSC.2307-5228.2019.11.1.62-67
18. Сентябов С.В., Карамнов Д.В. Методы определения первоначальных напряжений массива горных пород натурными измерениями. Проблемы недропользования. 2023;(1):54–63. https://doi.org/10.25635/2313-1586.2023.01.054 Sentyabov S.V., Karamnov D.V. Methods for determining the initial stresses of the rock massif by in-situ measurements. Problems of Subsoil Use. 2023;(1):54–63. (In Russ.) https://doi.org/10.25635/2313-1586.2023.01.054
19. Figueiredo B., Sjöberg J., Mattila J., Hakala M., Suikkanen J. Analysis and determination of the stress field at the Olkiluoto site. IOP Conference Series: Earth and Environmental Science. 2023;1124:012002. https://doi.org/10.1088/1755-1315/1124/1/012002
20. Мехеда В.А. Тензометрический метод измерения деформаций. Самара: Изд-во Самар. гос. аэрокосм. ун-та; 2011. 56 с. Режим доступа: https://sensor-sms.ru/f/tenzometricheskij_metod-meheda_va.pdf (дата обращения: 12.09.2024).
21. Кобаяси А. Экспериментальная механика. М.: Мир; 1990. Кн. 1. 552 с.
22. Пригоровский Н.И. Методы и средства определения полей деформаций и напряжений. М.: Машиностроение; 1983. 248 с. Режим доступа: https://djvu.online/file/Q8Fxta7aF3OAM (дата обращения: 12.09.2024).
23. Дайчик М.Л., Пригоровский Н.И., Хуршудов Г.Х. Методы и средства натурной тензометрии. М.: Машиностроение; 1989. 240 с. Режим доступа: https://djvu.online/file/Ec9tX4tOIwkWD (дата обращения: 12.09.2024).
24. Турчанинов И.А., Иванов В.И., Марков Г.А. Руководство по измерению напряжений в массиве скальных пород методом разгрузки: вариант торцевых измерений. Апатиты; 1970. 48 с.
25. Турчанинов И.А., Марков Г.А., Панин В.И., Иванов В.И. Экспериментальное определение полного тензора напряжений в массиве горных пород. Апатиты; 1973. 39 с.
26. Деменчук Н.П., Прилуцкий А.А. Основы теории напряженного и деформированного состояния. СПб.: Университет ИТМО; 2016. 118 с. Режим доступа: https://books.ifmo.ru/file/pdf/2098.pdf (дата обращения: 12.09.2024).
27. Реут Л.Е. Теория напряженного и деформированного состояния с примерами и задачами. Минск: БИТУ; 2008. 107 с. Режим доступа: https://rep.bntu.by/handle/data/3841 (дата обращения: 12.09.2024).
28. Водопьянов В.И., Савкин А.Н., Кондратьев О.В. Курс сопротивления материалов с примерами и задачами. Волгоград: ВолгГТУ; 2012. 136 с. Режим доступа: http://sopromat.vstu.ru/metod/sem/sem_11.pdf (дата обращения: 12.09.2024).
29. Каспарьян Э.В., Козырев А.А., Иофис М.А., Макаров А.Б. Геомеханика. М.: Высш. шк.; 2006. 503 с.
30. Bonnechere F. A comparative study of in situ rock stress measurements, M.S. Thesis, Univ. of Minnesota. 1967.
31. Van Heerden W. L. Determination of the accuracy of "doorstopper" stress measurements in coal, Rep. Coun. Scient. Ind. Res. S. Afr. 1968.








