Совершенствование алгоритма для расчета напряженно-деформированного состояния массива пород при измерении деформаций методом разгрузки напряжений на торце скважины

И.Э. Семенова1, П.В. Амосов2, Н.Н. Кузнецов1, В.А. Некрасов1
¹ Горный институт Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация
2 Институт проблем промышленной экологии Севера Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация
Russian Mining Industry №5/ 2025 p. 84-90

Резюме: Статья представляет собой продолжение изложения результатов исследований по расчету параметров напряженно-деформированного состояния массива пород на основе данных натурных измерений. Предложен алгоритм, позволяющий объединить подходы Горного института Кольского научного центра РАН и E.R. Leeman, для расчета напряжений, действующих в массиве пород и определяемых на основании данных, полученных методом разгрузки в варианте торцевых измерений. Приведен математический аппарат для расчета компонент тензора напряжений в плоскости поверхности забоя трех взаимно перпендикулярных скважин, когда выбор направлений двух из них совпадает с направлениями главных напряжений на торце забоя третьей скважины. Проанализирована ситуация использования четырехдатчиковой розетки для схемы размещения тензодатчиков с углами 0, 60, 120 и 90°. Представлены два возможных алгоритма расчета для вычисления нормальных компонент напряжений, а также результаты расчетов на базе экспериментальных данных, полученных при проведении измерений напряженно-деформированного состояния в массиве пород Ждановского месторождения. Выполнен сравнительный анализ полученных прогнозных значений максимальных и минимальных напряжений по критерию отклонения на ±10% от среднего. Применение метода наименьших квадратов дает значения максимальных и минимальных напряжений, близкие к результатам перебора 16 комбинаций.

Ключевые слова: напряженно-деформированное состояние, массив горных пород, метод полной разгрузки напряжений, скважина, розетка тензодатчиков

Для цитирования: Семенова И.Э., Амосов П.В., Кузнецов Н.Н., Некрасов В.А. Совершенствование алгоритма для расчета напряженно-деформированного состояния массива пород при измерении деформаций методом разгрузки напряжений на торце скважины. Горная промышленность. 2025;(5):84–90. https://doi.org/10.30686/1609-9192-2025-5-84-90

Информация о статье

Поступила в редакцию: 11.05.2025

Поступила после рецензирования: 09.07.2025

Принята к публикации: 14.07.2025

Информация об авторах

Семенова Инна Эриковна – кандидат технических наук, руководитель отдела геомеханики, Горный институт Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация; https://orcid.org/0000-0003-4074-7240 ; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Амосов Павел Васильевич – кандидат технических наук, ведущий научный сотрудник лаборатории междисциплинарных эколого-экономических исследований, Институт проблем промышленной экологии Севера Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация; https://orcid.org/0000-0002-7725-6261 ; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Кузнецов Николай Николаевич – кандидат технических наук, руководитель лаборатории инструментальных исследований состояния горных пород Арктической зоны РФ, отдел геомеханики, Горный институт Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация; https://orcid.org/0000-0002-0624-4351 ; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Некрасов Валерий Аркадьевич – ведущий инженер лаборатории инструментальных исследований состояния горных пород Арктической зоны РФ, отдел геомеханики, Горный институт Кольского научного центра Российской академии наук, г. Апатиты, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Введение

Оценка типа и параметров напряженно-деформированного состояния массива горных пород является необходимой при проектировании выемки запасов полезных ископаемых [1–4]. Дефицит информации о НДС может приводить как к необоснованному выбору системы разработки и ее параметров, так и к недостаточной проработке вопросов безопасности горных работ. Одним из методов натурных исследований НДС остается на протяжении нескольких десятилетий метод полной разгрузки [5–10].

В публикации [9] авторы, во многом опираясь на работы E.R. Leeman [11], А. Кобаяси [12] и ряд учебно-методических пособий [13–17], представили результаты своих исследований в части разработки математического аппарата для расчета напряжений, действующих в массиве пород и определяемых на основании метода разгрузки в варианте торцевых измерений. В частности, предложен подход для расчета компонент тензора напряжений в плоскости забоя трех взаимно перпендикулярных скважин (рис. 1, а) через величины деформаций четырехдатчиковой розетки для схемы размещения тензодатчиков [9] с углами равными βA = 0°, βB = 45°, βC = 90°, и βD = 135°.

Рис. 1. Компоненты нормальных и касательных напряжений по результатам замеров в трех взаимно ортогональных друг другу скважинах (1, 2, 3 – номер забоя скважин): а – схема по E.R. Leeman [11]; б – схема по E.R. Leeman [11], видоизмененная в соответствии с методикой Горного института [18; 19] в части выбора направлений скважин 1 и 2 посредством поворота вдоль главных напряжений σ1 и σ2 на торце скважины 3

Fig. 1. Components of normal and tangential stresses based on the results of measurements in three mutually orthogonal boreholes (1, 2, 3 – number of borehole bottom): а – layout by E.R. Leeman [11]; б – layout by E.R. Leeman [11], modified according to the methodology of the Mining Institute [18; 19] in terms of selecting the directions of Boreholes 1 and 2 by rotating along the main stresses σ1 and σ2 at the bottom of Borehole 3

Этот подход включает в себя алгоритм и математические формулы, используемые для перехода от направлений и величин напряжений на плоскости замеров к направлению и величинам главных напряжений в массиве.

Одновременно существует методика Горного института КНЦ РАН [18; 19] для решения аналогичной задачи. Особенность методики заключается в выборе направления скважин 1 и 2 вдоль действия главных напряжений σ1 и σ2 на торце скважины 3 (рис. 1, б). При этом и переход к напряжениям во вмещающем массиве выполняется по оригинальному алгоритму [18; 19], отличающемуся от алгоритма E.R. Leeman [11].

Назовем подход E.R. Leeman [11] «строгая ортогональность скважин», а подход ГоИ КНЦ РАН [18; 19] «квазиортогональность скважин», что обусловлено указанной выше особенностью.

Цель настоящей работы заключается в том, чтобы с использованием наработок подхода «квазиортогональности скважин» в части измерений на торцах всех трех скважин [18; 19] перейти к вычислениям напряжений во вмещающем массиве по алгоритму E.R. Leeman [11], т.е. подходу «строгой ортогональности скважин». Применение такого алгоритма позволит обойтись без дополнительных поправочных параметров, значения которых имеют разброс до 30% [9].

Расчет напряжений на торце скважин

Методика ГоИ КНЦ РАН предполагает использование четырехэлементной прямоугольной розетки с датчиками [9], расположенными под углами βA = 0°, βB = 60°, βC = 120° и βD = 90°, т.е. углу А соответствует направление 1, углу В направление 2, углу С направление 3 и углу D направление 4. Соответствующие данным углам значения косинусов и синусов:

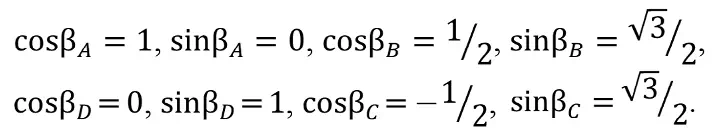
На основании измеренных в ходе разгрузки значений деформаций выполняется переход к напряжениям на забое скважины (плоское напряженное состояние) с использованием формул теории упругости [12–17].

Система уравнений преобразования деформаций при повороте осей координат в нашем случае имеет вид:

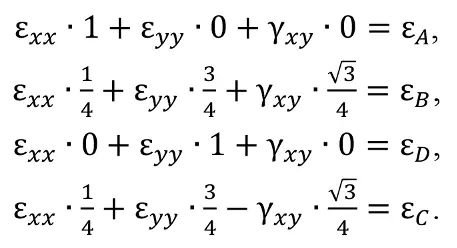
Из первых трех уравнений имеем:

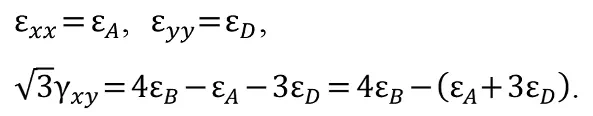
Если сложить 2-е и 4-е уравнения, то с учетом приведенных решений 2ε_A + 6ε_D = 4ε_B + 4ε_C или ε_A + 3ε_D = 2ε_B + 2ε_C, т.е. 3-ю компоненту деформаций можно записать в форме 

Таким образом, задействованы все 4 измеряемые деформации. По известным компонентам тензора деформаций главные деформации ε₁ и ε₂, а также их направления на забое скважины:

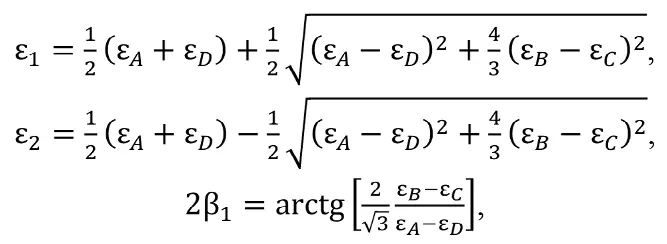
где β₁ – угол наклона деформации ε₁ к оси x. В отношении угла β₁ А. Кобаяси [12] обращает внимание, что на самом деле имеем два значения. Одно значение дает угол β₁ между ε₁ и осью x, а другое – угол β₂ между ε₂ и осью x. Следуя рекомендациям E.R. Leeman [11], введем необходимое в дальнейшем обозначение:

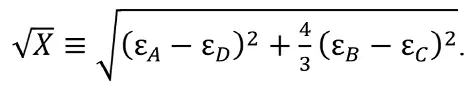
По известным главным деформациям ε₁ и ε₂ записываем главные напряжения σ₁ и σ₂ и максимальное тангенциальное напряжение τmax на торце скважины. Далее выражаем σ₁, σ₂, τmax через измеренные деформации:

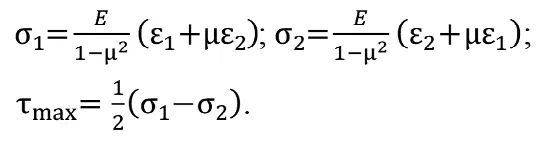
Следует обратить внимание, что в подходе «квазиортогональности скважин» для вертикальной оси Y будут использоваться именно эти величины:

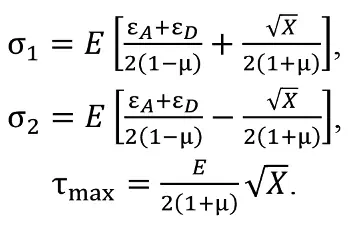
В подходе «строгой ортогональности скважин» по известным главным напряжениям записывают и далее используют компоненты напряжений по выбранным направлениям X и Y:

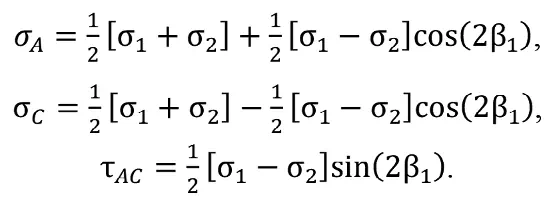
Выразим результат через измеренные деформации:

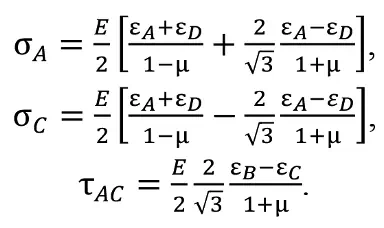
Таким образом, компоненты тензора напряжений в плоскости поверхности забоя скважин (1 и 2) через величины деформаций, полученные по четырем датчикам, определяются по следующим формулам:

– для скважины №1 (ось скважины совпадает с осью Z, см. рис. 1, а):

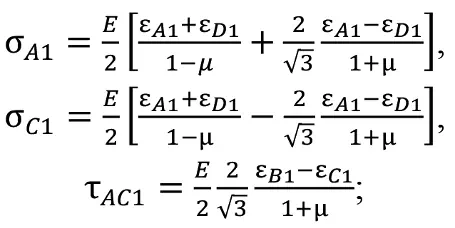
– для скважины №2 (ось скважины совпадает с осью X, см. рис. 1, а):

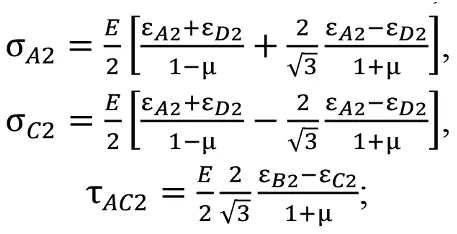
– для скважины №3 (ось скважины совпадает с осью Y, см. рис. 1, а) в подходе «строгой ортогональности скважин» имеем:

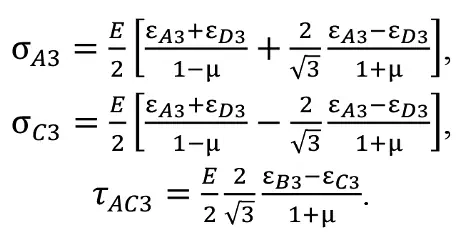
В подходе «квазиортогональности скважин», как указывалось выше, используем значения главных напряжений σ₁ и σ₂ и максимальное тангенциальное τmax на торце скважины (см. рис. 1, б)

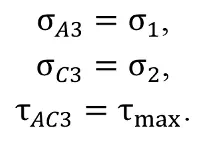
В правых частях уравнений фигурируют относительные деформации, полученные по соответствующему датчику деформаций, а для скважины №3 (ось скважины совпадает с осью Y) из первоначального эксперимента и обработки информации по этой (вертикальной) скважине.

Применение алгоритма E.R. Leeman для расчета напряжений в массиве

На шаге нахождения значений напряжений в массиве и углов наклона площадок главных напряжений, выраженных через направляющие косинусы, воспользуемся алгоритмом E.R. Leeman [11].

Запишем следующую систему уравнений, используя правило: 1-я скважина последовательность XYZ; 2-я скважина последовательность YZX и 3-я скважина последовательность ZXY. Присвоим всем уравнениям номера:

Путь 1. Рассмотрим классический подход, когда из представленной системы уравнений (1)–(6) выбираются 3 уравнения под 3 неизвестные нормальные компоненты напряжений σ_x, σ_y и σ_z.

Из шести уравнений по трем можно составить 16 комбинаций.

Во-первых, возможны 8 комбинаций, когда для создания системы уравнений задействованы только две скважины: I – 123; II – 124; III – 125; IV – 126; V – 134; VI – 234; VII – 345; VIII – 346.

Например, для комбинации 124 система необходимых определителей для вычисления нормальных компонент напряжений σx, σy и σz в породном массиве, составленная, например, из уравнений для скважин №1 – №2, имеет вид:

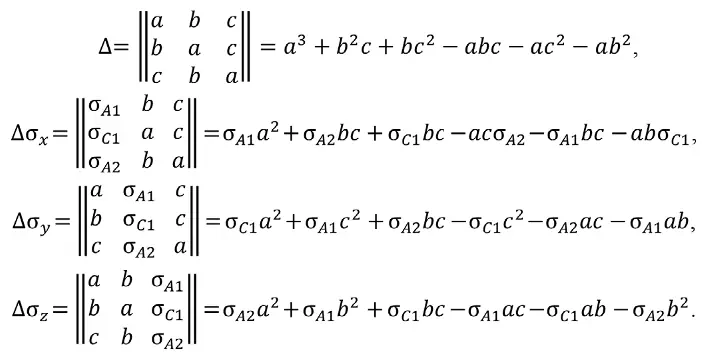
Во-вторых, возможны 8 комбинаций, когда одновременно задействованы по одному уравнению для каждой скважины: I – 135; II – 136; III – 145; IV – 146; V – 235; VI – 236; VII – 245; VIII – 246.

Например, для комбинации 135 система необходимых определителей для вычисления нормальных компонент напряжений σx, σy и σz в породном массиве, составленная, например, из уравнений для скважин №1–№2–№3, имеет вид:

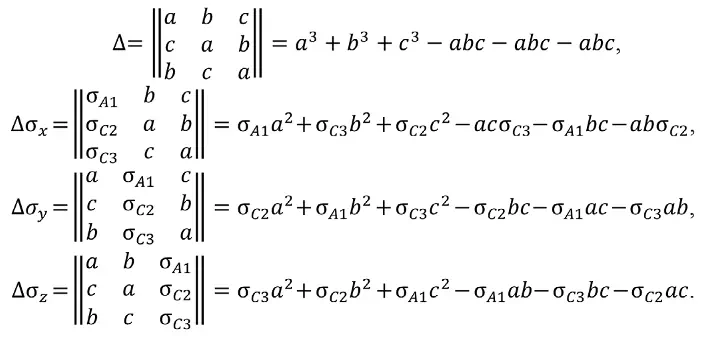
Во всех 16 комбинациях после вычисления определителей последовательно рассчитываем нормальные и касательные компоненты напряжений в массиве:

Запишем тензор компонент напряжений:

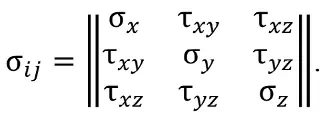
Строго говоря, наличие 16 комбинаций заставляет либо искать какой-то «однозначный» (Путь 2) выход из положения, либо выполнить анализ результатов расчетов всех 16 комбинаций, чтобы отсеять «нефизичные» решения, т.к. формально мы имеем переопределенную систему линейных алгебраических уравнений.

Путь 2. Для решения системы линейных алгебраических уравнений (1)–(6), состоящей из шести уравнений и содержащей три неизвестные, используем метод наименьших квадратов [20; 21]. Расчеты можно выполнить с использованием верифицированного программного обеспечения (например, компилятора MS Fortran Power Station 4.0 или др.).

Тестирование подхода «квазиортогональности скважин»

Исходные данные для поверочного расчета взяты по одной из замерных станций на Ждановском месторождении: модуль упругости равен 87,0 ГПа и коэффициент Пуассона равен 0,22, относительные деформации в скважинах по датчикам приведены в табл. 1.

Таблица 1 Относительные деформации в скважинах по датчикам
Table 1 Relative strains in boreholes by the strain gauges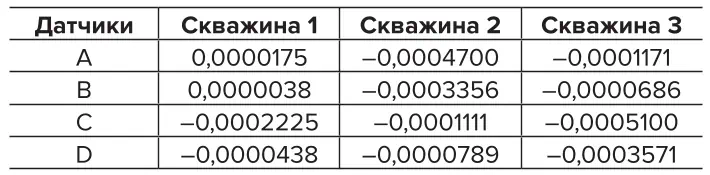

Для выполнения расчетов по Пути 1 и Пути 2 использованы программы, созданные в компиляторе MS Fortran Power Station 4.0. Результаты поверочных расчетов всех 16 комбинаций Пути 1 для минимальных и максимальных напряжений приведены в табл. 2. На данном этапе исследований акцентируем внимание только на напряжениях. На рис. 2 и 3 приведены графические изображения модулей минимальных и максимальных напряжений в форме диаграмм при использовании данных по двум и трем скважинам соответственно.

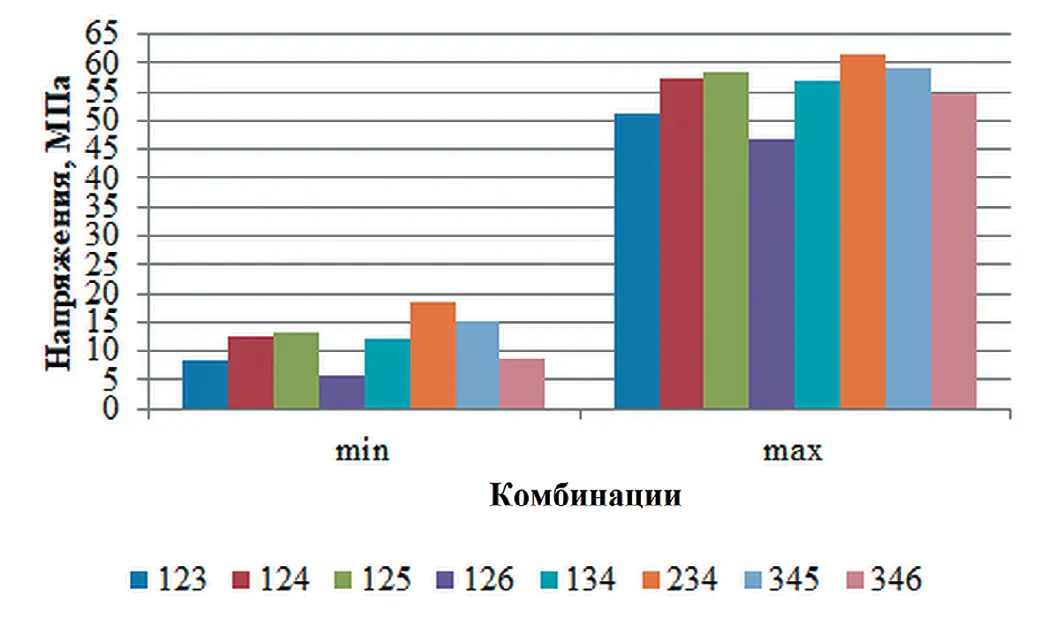Рис. 2 Диаграмма модулей минимальных и максимальных значений напряжений при использовании данных по двум скважинам

Fig. 2 A bar chart featuring the moduli of the minimum and maximum stress values using data from two boreholes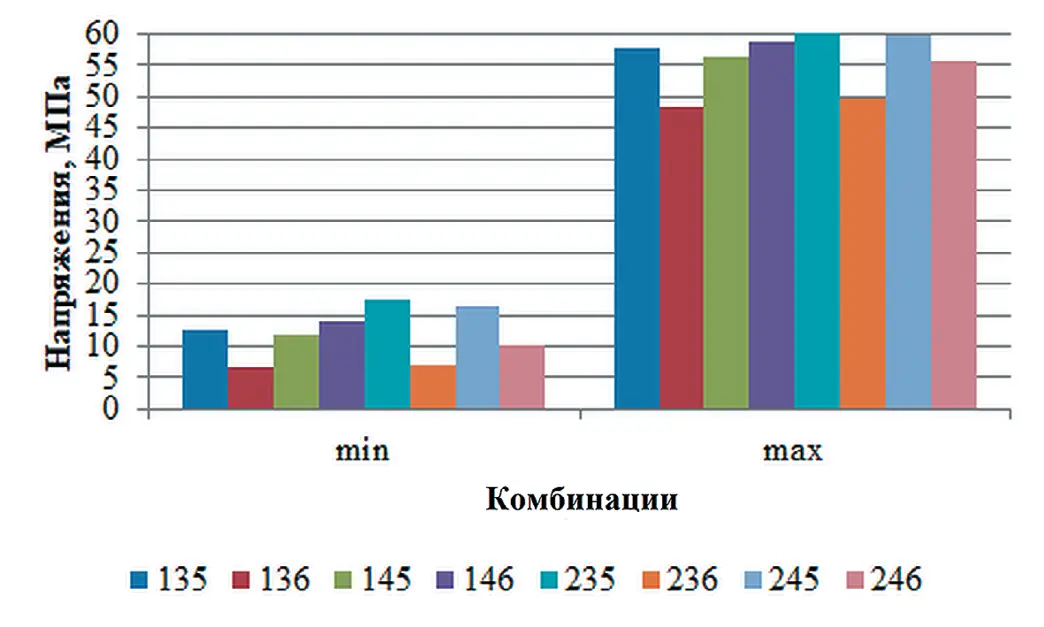Рис. 3 Диаграмма модулей минимальных и максимальных значений напряжений при использовании данных по трем скважинам

Fig. 3 A bar chart featuring the moduli of the minimum and maximum stress values using data from three boreholes

Данные табл. 2, рис. 2 и 3 свидетельствуют, что прогнозные значения напряжений имеют определенный разброс.

Таблица 2 Значения минимальных и максимальных напряжений (Путь 1)

Table 2 Minimum and maximum stress values (Path 1)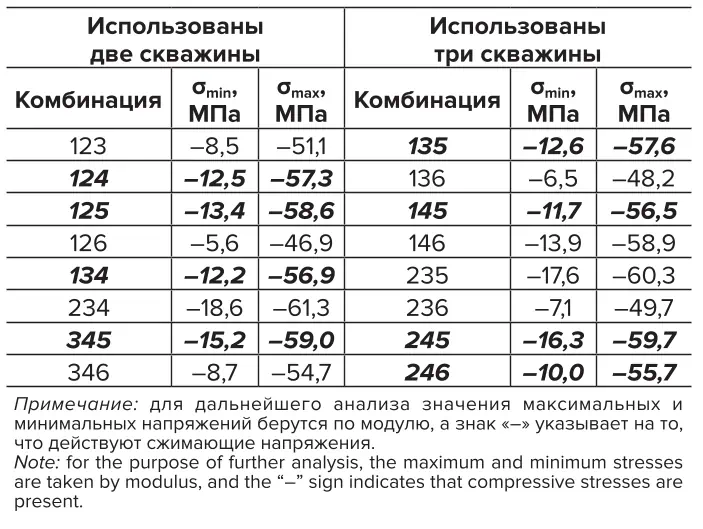

Обратимся к средним расчетным значениям. В принципе, здесь возможны два способа:

1) осреднение по всем 16 комбинациям;

2) осреднение по 8 комбинациям, которые в табл. 2 выделены полужирным шрифтом.

Первый способ является достаточно понятным, тогда как второй требует определенных разъяснений. Дело в том, что в комбинациях, которые в табл. 2 не выделены полужирным шрифтом, в правых частях системы трех уравнений в двух из них при рассмотрении элементарного кубика, т.е. переходе к бесконечно малым масштабам, появляются компланарные векторы, равные по модулю. Например, для комбинации 123 это будут σC(1) и σC(2) (см. рис. 1, а).

 Таблица 3 Осредненные расчетные значения минимальных и максимальных напряжений (Путь 1)

Table 3 Averaged calculated values of the minimum and maximum stresses (Path 1)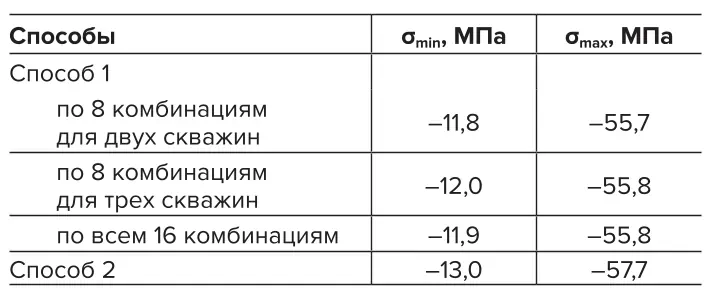

В табл. 3 представлены осредненные по описанным способам Пути 1 расчетные значения минимальных и максимальных напряжений. 

Попробуем найти комбинацию скважин, для которых выполняется условие отклонения от среднего значения примерно на ±10%, что соответствует требованиям точности расчетов в горном деле, достаточной при исследовании свойств и состояния массива пород [22]. В случае напряжений это составит для их максимальных значений примерно ±5 МПа, а для их минимальных значений примерно ±1 МПа.

В подходе способа 1 Пути 1 для максимальных и минимальных напряжений имеем:

– по двум скважинам: 124, 134 (минимальные) и 123, 124, 125, 134, 345, 346 (максимальные) (две общих комбинации: 124, 134);

– по трем скважинам: 135, 145 (минимальные) и 135, 145, 146, 235, 2

36, 246 (максимальные) (две общих комбинации: 135, 145). Таким образом, из анализа минимальных и максимальных напряжений по двум и трем скважинам способа 1 Пути 1 имеем следующие прогнозные значения:

– комбинация 124: –12,5 МПа и –57,3 МПа; комбинация 134: –12,2 МПа и –56,9 МПа;

– комбинация 135: –12,6 МПа и –57,6 МПа; комбинация 145: –11,7 МПа и –56,5 МПа.

Аналогичный анализ минимальных и максимальных напряжений на базе способа 2 Пути 1 дает следующие прогнозные значения:

– комбинация 124: –12,5 МПа и –57,3 МПа; комбинация 125: –13,4 МПа и –58,6 МПа;

– комбинация 134: –12,2 МПа и –56,9 МПа; комбинация 135: –12,6 МПа и –57,6 МПа.

Обобщая оба способа Пути 1, можно рекомендовать для вычислений минимальных и максимальных напряжений использовать комбинации 124, 134 и 135.

В результате численного решения системы уравнений (1)–(6) по Пути 2 получим искомые компоненты напряжений: минимальное –11,3 МПа и максимальное –5 6,6 МПа.

Видно, что результаты, полученные с использованием метода наименьших квадратов (Путь 2), находятся в хорошем, по крайней мере, инженерном, согласии (±10%) с результатами осреднения по классическому пути решения проблемы на базе способа 1, что вполне достаточно при исследовании свойств и состояния массива пород.

Заключение

Представлены алгоритм и математический аппарат, позволяющие объединить подход Горного института КНЦ РАН «квазиортогональности скважин» и подход E.R. Leeman «строгая ортогональность скважин», для расчета напряжений, действующих в массиве пород и определяемых на основании метода разгрузки в варианте торцевых измерений.

Предложен математический аппарат для расчета компонент тензора напряжений в плоскости поверхности забоя трех взаимно перпендикулярных скважин, когда выбор направлений двух из них совпадает с направлениями главных напряжений на торце забоя третьей скважины.

Алгоритм приведен через величины деформаций четырехдатчиковой розетки для схемы размещения тензодатчиков с углами βA = 0°, βB = 60°, βC = 120° и βD = 90°.

Описан подход, который включает в себя математические формулы и алгоритм перехода от направлений и величин напряжений на плоскости замеров к направлению и величине главных напряжений в массиве.

Для вычисления нормальных компонент напряжений σx, σy и σz представлены два из возможных алгоритмов расчета напряжений и углов наклона площадок в массиве: Путь 1 – классический, когда посредством перебора рассматриваются 16 комбинаций: три уравнения и три неизвестных (обсуждаются два способа выбора системы уравнений); Путь 2 – использование метода наименьших квадратов ко всем шести уравнениям с тремя неизвестными. Представлены результаты поверочных расчетов на основе набора экспериментальных данных, полученных при проведении разгрузки в массиве пород Ждановского месторождения.

Выполнен сравнительный анализ полученных прогнозных значений максимальных и минимальных напряжений по критерию отклонения на ±10% от среднего для обоих способов Пути 1. Отмечены хорошие совпадения результатов трех комбинаций по минимальным и максимальным напряжениям.

Показана хорошая сходимость значений максимальных и минимальных напряжений, полученных методом наименьших квадратов (Путь 2), с результатами при использовании классического подхода.

Список литературы

1. Козырев А.А., Панин В.И., Семенова И.Э. Опыт применения экспертных систем оценки напряженно-деформированного состояния массива горных пород для выбора безопасных способов отработки рудных месторождений. Записки Горного института. 2012;198:16–23. Режим доступа: https://pmi.spmi.ru/pmi/article/view/5908 (дата обращения: 27.04.2025). Kozyrev A.A., Panin V.I., Semenova I.E. Experience in expert systems application for estimation of stress- strain state of rock mass for selection of safe methods of ore deposits mining. Journal of Mining Institute. 2012;198:16–23. (In Russ.) Available at: https://pmi.spmi.ru/pmi/article/view/5908 (accessed: 27.04.2025).

2. Криницын Р.В. Напряженно-деформированное состояние массива горных пород при отработке месторождений Урала. Горная промышленность. 2022;(5):79–82. https://doi.org/10.30686/1609-9192-2022-5-79-82 Krinitsyn R.V. Stress-and-strain state of the rock mass in mining deposits in the Urals. Russian Mining Industry. 2022;(5):79– 82. (In Russ.) https://doi.org/10.30686/1609-9192-2022-5-79-82

3. Adah E.I., Amah E.A. Modified horizontal stress equations for rock mass insitu stress state. Nnamdi Azikiwe University Journal of Civil Engineering (NAUJCVE). 2024;2(3):11–14. Available at: https://naujcve.com/index.php/NAUJCVE/article/view/134/139 (accessed: 20.06.2025).

4. Demin V., Kalinin A., Tomilova N., Tomilov A., Akpanbayeva A., Shokarev D., Popov A. Advanced digital modeling of stressstrain behavior in rock masses to ensure stability of underground mine workings. Civil Engineering Journal. 2025;11(3):1072– 1087. https://doi.org/10.28991/CEJ-2025-011-03-014

5. Christiansson R., Janson T. A test of different stress measurement methods in two orthogonal bore holes in Äspö Hard Rock Laboratory (HRL), Sweden. International Journal of Rock Mechanics and Mining Sciences. 2003;40(7-8):1161–1172. https://doi.org/10.1016/j.ijrmms.2003.07.006

6. Yaméogo S.T., Corthésy R., Leite M.H. Influence of local heterogeneity on Doorstopper stress measurements. International Journal of Rock Mechanics and Mining Sciences. 2013;60:288–300. https://doi.org/10.1016/j.ijrmms.2013.01.001

7. Guido S., Acerbis R., Sossi G. Practice of the Doorstopper stress measurement method during the last 30 years in Italy. IOP Conference Series: Earth and Environmental Science. 2021;833:012167. https://doi.org/10.1088/1755-1315/833/1/012167

8. Feng Y., Pan P.-Z., Wang Z., Liu X., Miao S. A novel indirect optical method for rock stress measurement using microdeformation field analysis. Journal of Rock Mechanics and Geotechnical Engineering. 2024;16(9):3616–3628 https://doi.org/10.1016/j.jrmge.2023.10.011

9. Семенова И.Э., Амосов П.В., Кузнецов Н.Н., Некрасов В.А. Развитие подходов к расчету параметров напряженнодеформированного состояния массива пород по результатам измерений деформаций на торце скважины. Горная промышленность. 2024;(5S):122–129. https://doi.org/10.30686/1609-9192-2024-5S-122-129 Semenova I.E., Amosov P.V., Kuznetcov N.N., Nekrasov V.A. Development of approaches to calculation of the stress-strain state parameters of the rock mass based on the results of deformation measurements at the borehole bottom. Russian Mining Industry. 2024;(5S):122–129. (In Russ.) https://doi.org/10.30686/1609-9192-2024-5S-122-129

10. Ali Z., Karakus M., Nguyen G.D., Amrouch K. Secant modulus method: A simplified technique for measuring in situ stresses in rocks. Rock Mechanics and Rock Engineering. 2025;58(4):4263–4279. https://doi.org/10.1007/s00603-024-03953-z

11. Leeman E.R. The CSIR “doorstopper” and triaxial rock stress measuring instruments. Rock Mechanics. 1971;3(1):25–50. https://doi.org/10.1007/BF01243550

12. Кобаяси А. (ред.) Экспериментальная механика [пер. с англ. под ред. Б.Н. Ушакова]. М.: Мир; 1990. Кн. 1. 615 с. :

13. Мехеда В.А. Тензометрический метод измерения деформаций. Самара: Изд-во Самар. гос. аэрокосм. ун-та; 2011. 56 с.

14. Деменчук Н.П., Прилуцкий А.А. Основы теории напряженного и деформированного состояния. СПб.: Университет ИТМО; 2016. 118 с.

15. Реут Л.Е. Теория напряженного и деформированного состояния с примерами и задачами. Минск: БИТУ; 2008. 107 с.

16. Водопьянов В.И., Савкин А.Н., Кондратьев О.В. Курс сопротивления материалов с примерами и задачами. Волгоград: ВолгГТУ; 2012. 136 с.

17. Иофис М.А., Макаров А.Б., Каспарьян Э.В., Козырев А.А. Геомеханика и охрана объектов поверхности. М.: Высш. шк.; 2006. 503 с.

18. Турчанинов И.А., Иванов В.И., Марков Г.А. (сост.) Руководство по измерению напряжений в массиве скальных пород методом разгрузки: вариант торцевых измерений. Апатиты; 1970. 48 с.

19. Турчанинов И.А., Марков Г.А., Панин В.И., Иванов В.И. (сост.) Экспериментальное определение полного тензора напряжений в массиве горных пород. Апатиты; 1973. 37 с.

20. Мудров В.И., Кушко В.Л. Методы обработки измерений. М.: Сов. радио; 1976. 192 с.

21. Лоусон Ч., Хенсон Р. Численное решение задач метода наименьших квадратов [пер. с англ. Х.Д. Икрамова]. М.: Наука; 1986. 230 с.

22. Барон Л.И., Логунцов Б.М., Позин Е.З. Определение свойств горных пород. М.: Госгортехиздат; 1962. 332 с.