Численное моделирование изменения напряженно-деформированного в процессе отработки месторождения в программном комплексе CAE Fidesys с использованием функции пошагового расчета

DOI: http://dx.doi.org/10.30686/1609-9192-2020-2-110-114

М.А. Соннов¹, А.Е. Румянцев², А.В. Трофимов², В.Б. Вильчинский² ¹ ООО «Фидесис», г. Москва, Российская Федерация ² ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация Горная Промышленность №2 / 2020 стр. 110-114

Резюме: Добыча полезных ископаемых на больших глубинах обусловливает необходимость учёта физико-механических свойств пород, слагающих массив. В исследовании применен комплексный подход компьютерного моделирования, в котором учитывались эти свойства и выделялись домены на основе рейтинговых характеристик массива, которые принимались для моделирования в конечно-элементной постановке. Для этого применялся программный комплекс CAE Fidesys. Установлено, что в процессе отработки рудного тела возможно возникновение очагов пластических деформаций. Причём при движении фронта в юго-западном направлении в рудном теле на следующий год отработки деформации встречаются чаще и в большем количестве. Наличие очагов пластических деформаций говорит о возможных осложнениях отработки рудных тел, что может выражаться в частичном разрушении боков выработок, нарушении геометрии выработок, стрелянии и шелушении массива. Рекомендуется вести работы с предварительной разгрузкой массива бурением строчки разгрузочных скважин или другими эффективными способами, чтобы увести опорное давление вглубь массива для исключения вероятности хрупкого разрушения руды в процессе ведения очистных работ. Применение численного моделирования вместе с результатами геотехнических исследований массива дает весьма большие возможности для оценки устойчивости массива и прогнозирования возникновения осложнений в процессе отработки месторождений полезных ископаемых подземным способом.

Ключевые слова: геомеханика, геотехника, рудный массив, тело, напряженно-деформированное состояние, массив горных пород, конечно-элементное моделирование, CAE Fidesys, AutoCAD, месторождение, физико-механические свойства, граничные условия, пластические деформации, обрушение

Для цитирования: Соннов М.А., Румянцев А.Е., Трофимов А.В., Вильчинский В.Б. Численное моделирование изменения напряженно-деформированного в процессе отработки месторождения в программном комплексе CAE Fidesys с использованием функции пошагового расчета. Горная промышленность. 2020;(2):110-114. DOI: 10.30686/1609-9192-2020-2-110-114.

Информация о статье

Поступила в редакцию: 07.04.2020

Поступила после рецензирования: 14.04.2020

Принята к публикации: 21.04.2020

Информация об авторах

Соннов Максим Александрович – заместитель генерального директора ООО «Фидесис», г. Москва, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript..

Румянцев Александр Евгеньевич – кандидат технических наук, ведущий научный сотрудник, ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация; ORCID: 0000-0002-2204-961X; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript..

Трофимов Андрей Викторович – кандидат технических наук, заведующий центром физико-механических исследований, ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация; ORCID: 0000-0001-7557-9801 e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript..

Вильчинский Владислав Борисович – кандидат технических наук, заведующий горной лабораторией, ООО «Институт Гипроникель», г. Санкт-Петербург, Российская Федерация; e-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript..

Введение

Ведение работ по добыче полезных ископаемых (руды) на больших глубинах обусловливает необходимость учёта напряжённо-деформированного состояния (НДС) массива горных пород, способов управления НДС массива, определения оптимальных параметров систем отработки, расчёта устойчивости рудного массива и вмещающих пород. Перечисленные задачи до начала отработки месторождения можно укрупненно оценить с помощью компьютерного моделирования.

В работе применен комплексный подход, в котором учитывались физико-механические свойства пород, слагающих массив, и выделялись домены на основе рейтинговых характеристик массива, которые принимались для моделирования в конечно-элементной постановке.

Одним из наиболее эффективных способов моделирования является применение пакетов конечно-элементного моделирования, которые широко используются в последние несколько десятилетий благодаря прогрессу в вычислительной мощности [1].

В приведённой работе применялся программный комплекс CAE Fidesys [2], который относительно недавно появился на рынке, но уже зарекомендовал себя как надёжный инструмент при решении задач механики деформируемого твёрдого тела.

Дополнительный модуль Fidesys Dynamics расширяет функционал CAE Fidesys возможностью расчетов нестационарных задач с быстропротекающими процессами, требующих особой точности, методом спектральных элементов. Продукт позволяет решать задачи моделирования неразрушающего контроля, распространения упругих колебаний в твердых телах, высокоточного описания волновых процессов. В CAE Fidesys для распараллеливания вычислений реализованы технологии OpenMP и MPI.

Моделирование

Рассматривается задача укрупненного моделирования процесса отработки месторождения полезного ископаемого с учётом морфологических особенностей и календарного графика, в задачах подобного рода в процессе нагружения в теле происходит перераспределение конечных деформаций. Основным их отличием, с точки зрения решения, от задач, решаемых в рамках стандартной «нелинейной теории», является необходимость решения системы нелинейных дифференциальных уравнений в частных производных для нескольких векторов перемещений [3].

Моделирование задач геомеханики связано с большими объемами вычислений. Определяется это в первую очередь значительными размерами моделируемых участков с повышением точности разбиения модели на конечные элементы в интересующих областях.

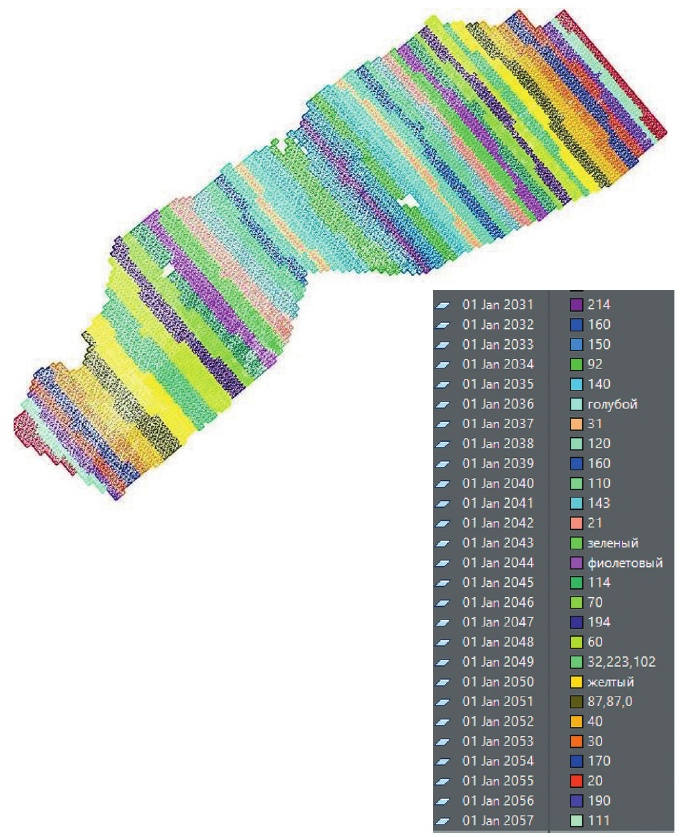
Рис. 1 Календарный план горных работ
Fig. 1 Mining operations schedule

Объёмная твердотельная модель, состоящая из рудного массива, обрушения (мб обрушенного) породного массива и необрушенного массива, строилась в среде AutoCad до дневной поверхности. В соответствии с календарным планом (рис. 1) модель разбивалась на отдельные объемы, где каждый объём соответствует году выемки (рис. 2).

Рис. 2 3D модель месторождения
Fig. 2 3D deposit model

Мощность зоны обрушенных пород равняется в среднем 10 мощностям рудного тела.

Так как отработка рудного тела осуществляется с обрушением вышележащих пород, то моделирование НДС массива реализовано в несколько этапов:

– на первом шаге определено изначальное НДС массива без выемки рудного тела;

– на втором шаге осуществлена выемка рудного тела в соответствии с календарным планом по годам;

– на третьем шаге путём замены физико-механических свойств моделируется разрушенный массив, который заполняет выработанное пространство, и обрушенный массив, мощность которого примерно равна 10 мощностям рудного тела, одновременно происходит выемка руды следующего календарного года;

– шаги 2 и 3 повторяются в соответствии с календарным планом на 29 лет до полной отработки.

Физико-механические свойства породного и рудного массива определялись с учётом рейтинговых показателей, полученных из блочной модели.

В численной модели рассматриваются 4 типа физико-механических свойств массивов горных пород: породный массив, порода разупрочнённая, порода обрушенная, рудный массив. В табл. 1 представлены физико-механические свойства породы и руды.

Известными параметрами для породного и рудного массивов являются Q’, σ_{сж, ρ}, параметры E, ν, C, β рассчитываются по следующим зависимостям [4; 5].

Для определения физико-механических характеристик разупрочнённой породы применена методика, приведённая в [6; 7], где коэффициент ослабления не превышает 0,25, для определения физико-механических характеристик обрушенной породы, когда сеть трещин превращается в хаотическую и массив приобретает свойства сыпучей среды, коэффициент ослабления не превышает 0,05.

Для определения удельного веса разупрочнённой породы и обрушенной породы коэффициенты разрыхления 1,04 и 1,1 соответственно.

Переход к прочности на одноосное сжатие обрушенной породы σсж(обр.) и разупрочненному массивам выполнен по формулам (1) и (2):

σ_{сж(обр.)} = 0,05 · σ_сж; (1)

σ_{сж(разупр.)} = 0,25 · σ_сж. (2)

Поскольку геотехническое описание керна выполнено по системе Бартона, выполнена конвертация рейтинга Qprime в систему GSI Хука Брауна по известной зависимости (3), а также рассчитан предел прочности массива на сжатие по зависимости (4):

GSI = 9 · LN(Q^') + 44; (3)

G_mGSI = 0,036 ∙ σs · e^GSI/30. (4)

Модуль деформации, сцепление, коэффициент Пуассона и угол дилатансии для массива определены по зависимостям (5-8):

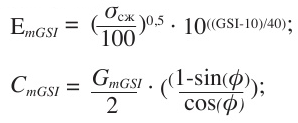
ν = 0,25 · (1 + e^(-G_mGSI/4) ); (7)

β = arctg(sin(φ)). (8)

Расчет производился в упругопластической постановке по модели пластичности Друкера-Прагера, в расчёте введены параметры сцепления и угла внутреннего трения.

Такая постановка является обязательной для подобных расчетов, т.к. возникновение зон пластических деформаций в расчетных моделях, говорит о возможных осложнениях отработки рудных тел и позволяет выбрать наиболее оптимальный способ отработки.

Весьма важным фактором при задании граничных условий является учет исходного напряженного состояния массива. При выполнении данных расчетов принималось исходное поле напряжений в соответствии с гипотезой А.Н. Динника, где горизонтальные напряжения не равны вертикальному и составляют лишь какую-то его часть, т.е. реакция массива на действие гравитационных сил.

После импорта модели в среду CAE Fidesys над ней проводился ряд булевых операций, а также операции по регуляризации и оптимизации объемов и их сращивание.

Размеры модели для исключения влияния границ принимались по осям: x-8000 м, y-6000 м, z-1100 м.

На отстроенной модели с использованием адаптивного генератора геометрии неструктурированных сеток создана конечно-элементная сетка для решения системы линейных алгебраических уравнений методом конечных элементов.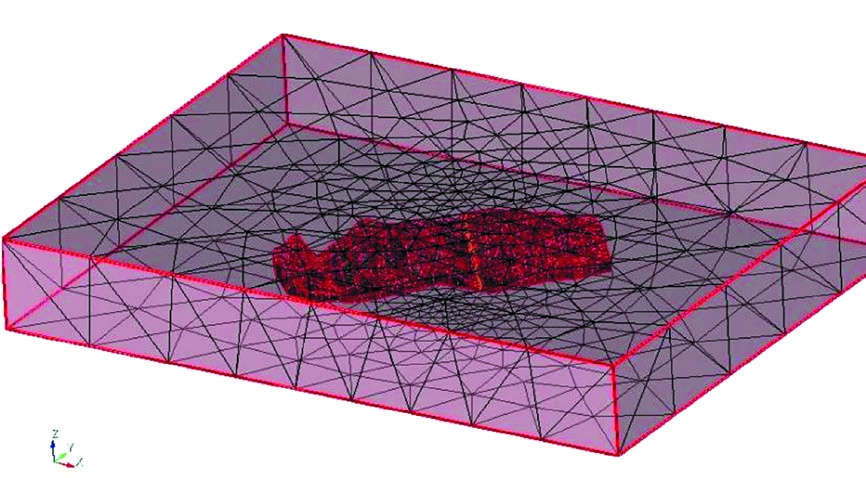


Рис. 3 Разбиение модели на конечные элементы

Fig. 3 Model breakdown into finite elements

Пример разбиения модели на конечные элементы представлен на рис. 3 и 4, количество элементов составляет 300 000, 80% которых сосредоточено в рассматриваемой области.

Рис. 4 Конечно-элементная сеть на объемах руды и блоках обрушения
Fig. 4 Finite element network for ore volumes and caving blocks

Затем каждому объему задаётся блок, различающийся по физико-механическим свойствам, после чего накладываются граничные условия, которые включают в себя:

– запрещение перемещений по всем направлениям для нижней плоскости модели;

– запрещение перемещений для боковых граней модели по соответствующим осям;

– для всей модели задается действие гравитации;

– в соответствии с поставленной задачей для блоков в модели задаются шаги нагружения (когда и какие блоки активны и, наоборот, на каких шагах происходит замена физико-механических свойств), всего 29 шагов (рис. 5);

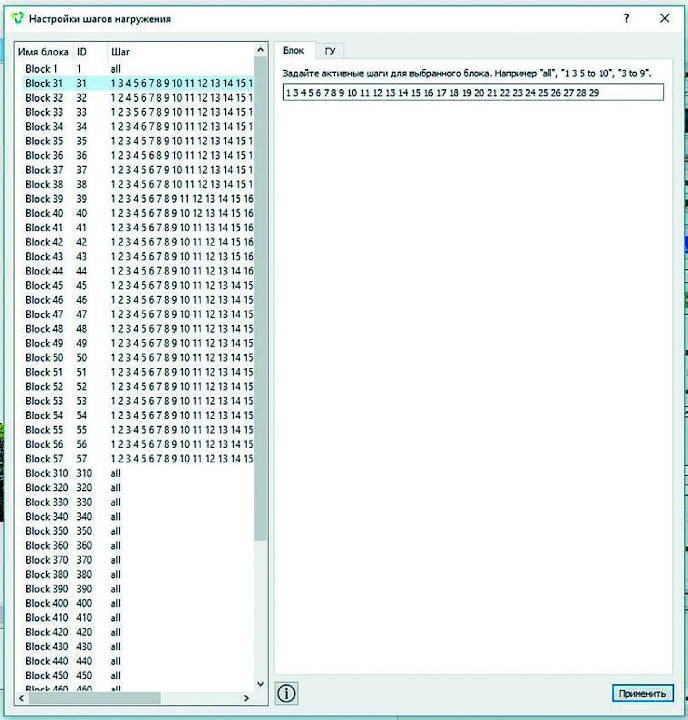
Рис. 5 Пример задания шагов нагружения в препроцессоре CAE Fidesys
Fig. 5 Example of load increment setting in the CAE Fidesys Preprocessor

– на каждом шаге блоку присваиваются уникальные физико-механические свойства в табличной форме по «квазивремени».

После проделанных подготовительных операций запускается расчет модели в упругопластической постановке.

Результаты моделирования последовательной выемки руды с обрушением горных пород

Следует отметить, что в процессе моделирования выемка рудного тела по годам осуществляется одним шагом за год, без дополнительной разбивки внутри года, т.к. целью моделирования является выявление наиболее опасных участков с точки зрения возникающих напряжений, в которых могут формироваться очаги пластических деформаций, что свидетельствует о нахождении части массива в запредельном состоянии.

В основном анализировались картины распределения напряжений и пластических деформаций по Мизесу. Напряжения, по Мизесу, представляют собой так называемую четвёртую теорию прочности, которая учитывает все главные напряжения; в этом случае сочетание компонентов напряжения приводится к одному эквивалентному напряжению, которое можно считать реальным напряженным состоянием, и выражается в виде:

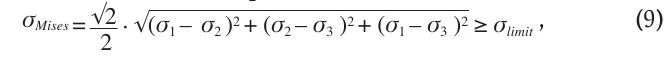
где σ_limit – критерий, по которому осуществляется сравнение напряжений.

Таким критерием может быть интерпретация критерия удароопасности из «Положения по безопасному ведению горных работ на месторождениях, склонных и опасных по горным ударам» (Федеральные нормы и правила в области промышленной безопасности «Положения по безопасному ведению горных работ на месторождениях, склонных и опасных по горным ударам». Режим доступа: https://meganorm.ru/Data2/1/4293771/4293771107.pdf ), где σ_(1(max) ≥ 0,7 · σ_сж.

В результате расчётов получены объёмные картины распределения напряжений и пластических деформаций на каждом шаге нагружения, результат расчёта занимает порядка 100 Гб памяти жёсткого диска. Приведём некоторые результаты расчётов.

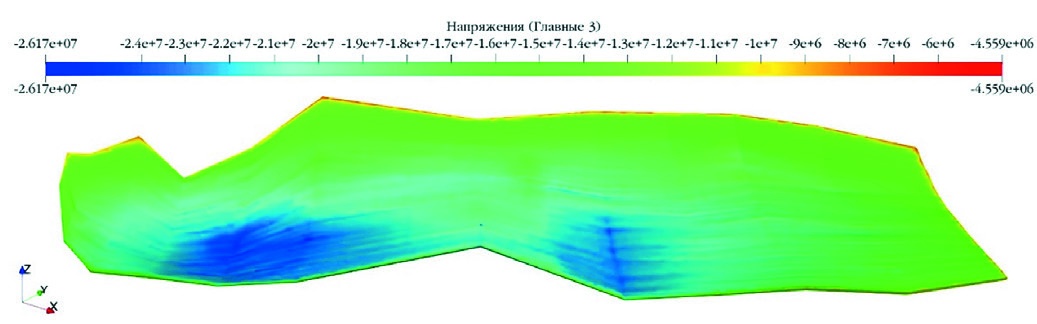
Рис. 6 Распределение максимальных главных напряжений в нетронутом массиве
Fig. 6 Distribution of maximum principal stresses in intact rock mass

Распределение максимальных главных напряжений в нетронутом массиве приведено на рис. 6. Распределение напряжений на 6-м шаге расчёта представлено на рис. 7 и 8. На 6-м шаге (см. рис. 7) расчёта напряжения в опорных областях достигают 45–50 МПа, в планируемом к отработке массиве на 2036 год наблюдаются очаги пластических деформаций.

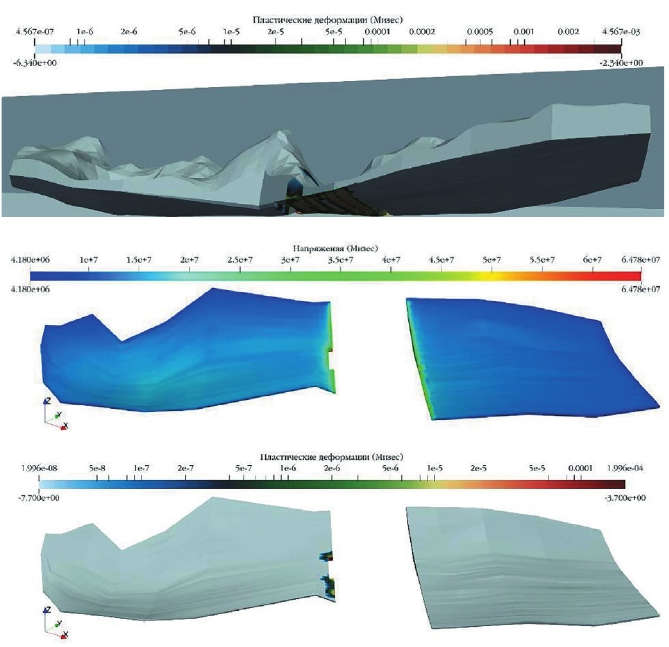
Рис. 7 Распределение напряжений на 6-м шаге расчёта
Fig. 7 Distribution of stresses in the 6th calculation step

На 6-м шаге (см. рис. 8) в рудном теле на 2036 год верхний рисунок в направлении СВ пластических деформаций не наблюдается, нижний рисунок в направлении ЮЗ присутствуют пластические деформации в кровле и боку рудного тела. Наличие пластических деформаций в обрушенной породе объясняется низкими физико-механическими её свойствами.

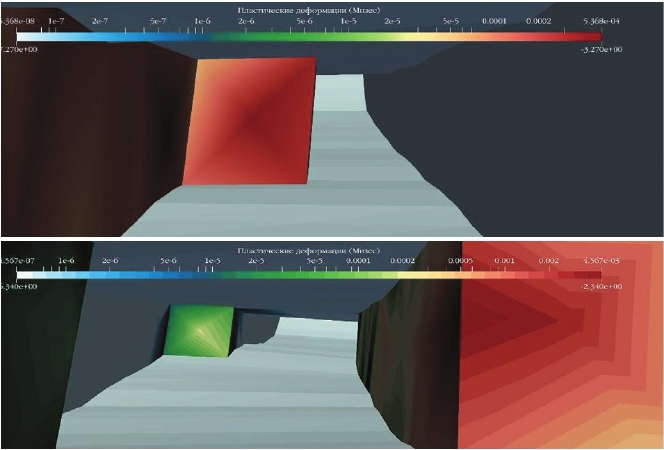
Рис. 8 Распределение напряжений на 6-м шаге расчёта
Fig. 8 Distribution of stresses in the 6th calculation step

Заключение

Следует отметить, что моделирование проведено с учётом сведений о горном массиве, которые имеются на момент выполнения расчёта. В перспективе с появлением новых данных о структурах, физико-механических свойствах, гидрогеологических и других характеристиках необходимо производить более подробное моделирование с уменьшением размера расчётной области с одновременным повышением точности расчёта путём сгущения конечно-элементной сетки или увеличения порядка элементов с переходом к спектральному анализу.

Установлено, что в процессе отработки рудного тела возможно возникновение очагов пластических деформаций, причём при движении фронта в юго-западном направлении в рудном теле на следующий год отработки в соответствии с календарным планом эти деформации встречаются чаще и в большем количестве. Пластические деформации идут нарастающим порядком в юго-восточном направлении от разрезки, в том числе и в разупрочнённом массиве (в среднем 10 мощностей отработанного рудного тела).

Наличие очагов пластических деформаций говорит о возможных осложнениях отработки рудных тел, что может выражаться в частичном разрушении боков выработок, нарушении геометрии выработок, стрелянии и шелушении массива.

Таким образом, рекомендуется вести работы с предварительной разгрузкой массива бурением строчки разгрузочных скважин или другими эффективными способами, чтобы увести опорное давление вглубь массива для исключения вероятности хрупкого разрушения руды в процессе ведения очистных работ.

Как видно, применение численного моделирования вкупе с результатами геотехнических исследований массива дает весьма большие возможности для оценки устойчивости массива и прогнозирования возникновения осложнений в процессе отработки месторождений полезных ископаемых подземным способом.

Список литературы

1. Соннов М.А., Румянцев А.Е., Трофимов А.В., Вильчинский В.Б. Геотехническое обоснование отработки залежей, ограниченных тектоническими нарушениями на основе применения конечно-элементного моделирования. Горная промышленность. 2018;(5):107–110. DOI: 10.30686/1609-9192-2018-5-141-107-110.

2. Вершинин А.В., Левин В.А., Морозов Е.М. Прочностной анализ: Фидесис в руках инженера. М.: ЛЕНАНД; 2015.

3. Левин В.А. Нелинейная вычислительная механика прочности. Т. 1. Модели и методы образования и развития дефектов. М.: ФИЗМАТЛИТ; 2015.

4. Селезнёв В.Е., Алёшин В.В., Прялов С.Н. Математическое моделирование трубопроводных сетей и систем каналов. Методы, модели и алгоритмы. М.: МАКС Пресс; 2007.

5. Vasarhelyi B., Kovacs D. Empirical methods of calculating the mechanical parameters of the rock mass. Periodica Polytechnica Civil Engineering. 2017;61(1):39–50. DOI: 10.3311/PPci.10095.

6. Борщ-Компониец В.И., Макаров А.Б. Горное давление при отработке мощных пологих рудных залежей. М.: Недра; 1986.

7. Заборщик М.П., Назименко В.В. Свойства пород зон разгрузки. Режим доступа: http://ea.donntu.edu.ua/handle/123456789/16177