Обзор моделей диспетчеризации карьерного автотранспорта

Введение

Известно, что горнодобывающие предприятия, и в особенности карьеры, требуют больших вложений как в капитальной, так и в эксплуатационной части. Технологический погрузочно-транспортный процесс на карьере как основной потребитель эксплуатационных расходов играет решающую роль в процессе принятия управленческих решений. Большая часть общих затрат на добычу полезных ископаемых в карьере должна быть направлена на извлечение и транспортировку извлеченной горной массы из забоев в различные места назначения за пределами карьера. По мнению многих исследователей, 50% эксплуатационных расходов (а в крупных карьерах – даже до 60%) приходится на погрузочно-транспортные работы. Таким образом, совершенствование погрузочно-транспортных операций и снижение эксплуатационных затрат на них хотя бы на 2–3% сэкономит акционерам огромные деньги.

Есть два основных способа повысить эффективность транспортирования горной массы в карьерах. Первый – использовать карьерные самосвалы особо большой грузоподъемности, способные перевозить больше с каждой загрузкой [1–3]. Второй способ улучшить транспортную работу и снизить затраты на тонну транспортируемого материала – внедрение методов исследования операций для повышения производительности работы. Несмотря на то что существуют одноуровневые подходы к оптимизации работы карьера, в которых реализуются непрерывные алгоритмы для максимизации производительности и направления самосвалов в места назначения так, чтобы одновременно сократить отставание от производственного плана, более интересен мультиуровневый подход, обычно разделяемый на две части (или два уровня).

В первой части с помощью методов статического планирования определяются: оптимальное расположение погрузочных средств в забоях, оптимальные грузопотоки для каждого маршрута, соединяющего пункты погрузки и разгрузки, а также первичная расстановка транспорта для достижения оптимальных грузопотоков. Задача этого уровня, называемого верхним, должна решаться в начале каждой смены или при изменении статуса карьера.

Во второй части (на нижнем уровне) специальный алгоритм адресует самосвалы в подходящие пункты назначения в тот момент, когда они запрашивают назначение, таким образом, чтобы минимизировать отклонение от плановых установок верхнего уровня.

1. Определение задачи производственного планирования на карьерах

Производственный план карьера, в зависимости от горизонта планирования, может быть трех видов: 1 – долгосрочный (от 20 до 30 лет, описывает осуществимость проекта добычи и распределение финансовых потоков, является основным входом в средне- и краткосрочный планы); 2 – среднесрочный (от 1 до 5 лет, дает более подробную информацию об отработке горных участков, в частности, о расширении парка или замене оборудования); 3 – краткосрочный (от 1 до 12 месяцев, дает детальную информацию об участках, подлежащих отработке, и рудопотоках для отправки на обогатительную фабрику). Краткосрочный план разбивается на оперативные планы. Оперативный план на смену – это базовый этап производственного планирования карьера, представляющий собой динамический процесс принятия решений в реальном времени работы карьера и включающий в себя следующие этапы: поиск кратчайших путей между пунктами погрузки и разгрузки; оптимизацию выработки, что означает определение оптимального грузопотока и первичную расстановку самосвалов по каждому маршруту так, чтобы достичь оптимального грузопотока (верхний уровень); и динамическое назначение, или диспетчеризацию, самосвалов (нижний уровень) (рис. 1).

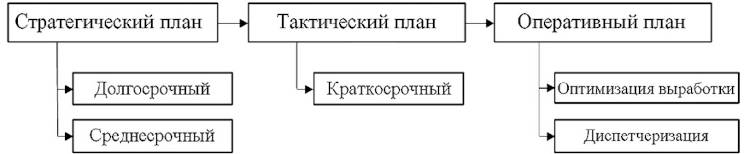Рис. 1 Стадии принятия решений при производственном планировании на карьере

Fig. 1 Stages of making decisions in mine production scheduling

То есть задача оперативного планирования связана с распределением оборудования и заключается в принятии решений о первичной расстановке и динамическом распределении самосвалов на основе пропускной способности маршрутов и возможностей оборудования.

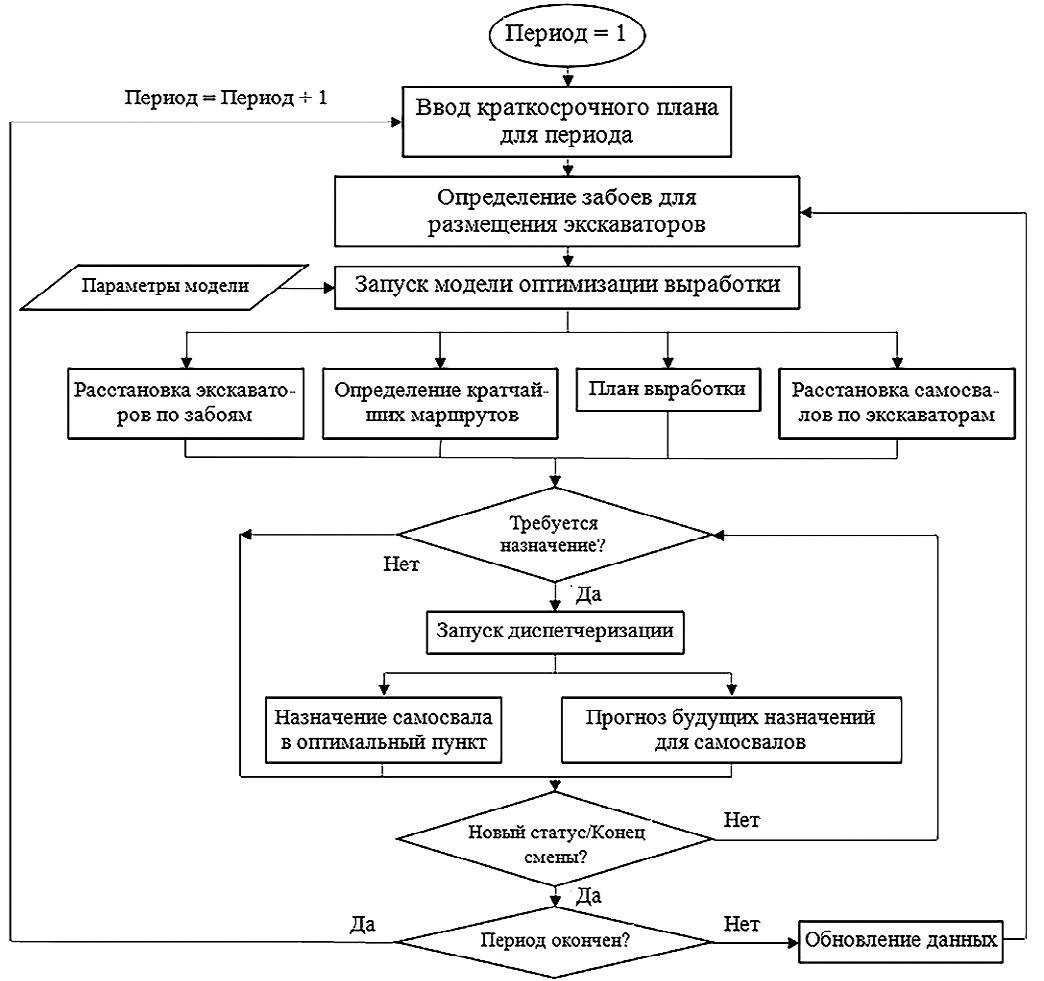Рис. 2 Схема процесса оперативного планирования работы карьера

Fig. 2 Schematic illustration of open pit mine operational plan

Оперативный план, схема которого представлена на рис. 2, принимает краткосрочный план каждого периода как руководство к действию и длится до окончания рабочей смены или до момента существенного изменения в структуре карьера.

В работе [4] предлагается следующая укрупненная классификация методов оперативного планирования.

Эвристические принципы. При принятии решения о назначении самосвала вызывается заранее выбранное эвристическое правило. Если правило требует, скажем, минимизации времени ожидания экскаватора, самосвал, запрашивающий назначение, будет направлен к экскаватору, который простаивает дольше всего, или к экскаватору, который, как ожидается, начнет простаивать первым, если все экскаваторы в данный момент заняты. Известно несколько таких эвристических принципов, и некоторым из распространенных были даны названия, такие как «минимальное время ожидания самосвала», «минимальное время ожидания экскаватора», «минимальное время цикла самосвала», «фиксированное назначение» и т.д.

Эвристические принципы обычно применяются к одному самосвалу за одно назначение. То есть текущее решение о назначении самосвала принимается безразлично к назначениям других самосвалов, которые будут сделаны в ближайшем будущем. Это часто приводит к недальновидным решениям, которые могут повысить мгновенную эффективность назначенных самосвалов, но снизить их эффективность в долгосрочной перспективе. Кроме того, почти все эвристические принципы игнорируют существенные ограничения или второстепенные цели работы экскаваторно-автомобильных комплексов (ЭАК), такие как соблюдение требований к качеству горной массы.

Системы с планом. Имеют двухкомпонентную структуру. Первый компонент связан с краткосрочным планированием производства, а основой для составления плана является модель математического программирования. Обычно пытаются максимизировать общие объемы добычи с учетом эксплуатационных ограничений, таких как целевое качество руды. Модель учитывает эксплуатационные характеристики, определяющие производственные возможности: скорость копания экскаваторов, размер доступного автопарка, конфигурация технологических трасс и время пробегов, вместимость рабочих зон, таких как отвалы и дробилки, и т. д. Модель программирования определяет то, что далее будет называться стационарным планом распределения грузопотоков (СПРГ), и этот план впоследствии используется как основа для принятия решений по распределению самосвалов в реальном времени.

Второй компонент – это процедура диспетчеризации, используемая для принятия решений о назначении самосвалов в реальном времени. Основная цель этого компонента – реализация целевых показателей, установленных СПРГ. Решения о назначении самосвалов основаны на отклонении текущего состояния системы от предписанного плана. В отличие от эвристических систем, системы с планом обычно рассматривают текущие и будущие решения о назначении самосвалов коллективно, хотя к этой задаче применялись разные подходы.

Назначения с ограничениями. В этих методах СПРГ отсутствует. Вместо этого решения о назначении самосвалов принимаются путем решения в реальном времени задач, формулировки которых пытаются оптимизировать производительность за счет сведения к минимуму времени ожидания самосвалов и экскаваторов. Подобно системам с планом, эти методы рассматривают вопрос назначения для самосвала в сочетании с назначениями для других самосвалов, которые, вероятно, будут сделаны в ближайшем будущем. Производственные ограничения, такие как требования к качеству продукции, встроены в критерии назначения самосвалов и ограничивают каждое решение о назначении.

Системы с планом интуитивно кажутся более точными и оттого предпочтительными (поскольку учитывают больше различной производственной информации) и наиболее распространены в настоящее время – как практически, так и теоретически.

Классификация методов, предлагаемая авторами работы [5], следующая.

«1 самосвал для N экскаваторов». После запроса нового назначения от самосвала, который может быть направлен к N экскаваторам, алгоритм оценивает возможные издержки или выгоды от назначения самосвала к каждому из этих экскаваторов – согласно заранее выбранному критерию. После оценки самосвал назначается к тому экскаватору, который, как ожидается, даст либо минимальные издержки, либо максимальную выгоду. Процесс повторяется при каждом запросе назначения самосвалом. Игнорируется влияние решения по текущему назначению самосвала на последующие назначения.

Это простейшая и старейшая методика диспетчеризации, она наиболее распространена в литературе и обычно реализуется через одноуровневый подход. В этих методах используются самые разные критерии, но цель их одинакова – максимизация производительности. В работе [4] отмечается, что какой бы критерий ни использовался в конкретной системе, недостатки есть всегда. К примеру, критерий минимального времени ожидания самосвала не должен использоваться при недостатке самосвалов в карьере. По этому критерию самосвал будет направлен к экскаватору, дающему наименьшее ожидаемое время простоя для самосвала. Вероятность возникновения очередей в недогруженных ЭАК мала, поэтому можно с равным успехом направить самосвал к любому экскаватору. Аналогично критерий минимального времени ожидания экскаватора будет неэффективен в перегруженных ЭАК, поскольку низка вероятность простоев экскаваторов. Также невозможно выбрать один из критериев диспетчеризации, который был бы однозначно эффективнее остальных во всех случаях.

Все зависит от текущего состояния ЭАК карьера.

Эти недостатки являются следствием недостаточно глобального взгляда на проблему диспетчеризации карьерного автотранспорта, поскольку в расчет принимается лишь один самосвал за одно назначение. Каждый из критериев диспетчеризации, встречающихся в известных работах, затрагивает лишь один конкретный аспект, например, простои самосвалов или простои экскаваторов. Поэтому методы диспетчеризации в рамках стратегии «1 самосвал для N экскаваторов» можно назвать недальновидными. Кроме того, не существует эффективного принципа, позволяющего определить наилучший из существующих критериев, и поэтому при выборе приходится опираться на некоторые эвристические принципы.

«М самосвалов для 1 экскаватора». Решения по адресации самосвалов будут приниматься при взятии в расчет М самосвалов, которые должны быть назначены в ближайшем будущем, но только для одного экскаватора за одно назначение. Вначале экскаваторы ранжируются по показателю, характеризующему их отставание от производственного плана. Затем, рассматривая каждый экскаватор в этой группе, направляют к конкретному экскаватору самосвал, который сократит это отставание.

В литературе удалось найти лишь один метод диспетчеризации в рамках этой стратегии: он был разработан для реальной системы диспетчеризации DISPATCH компании Modular Mining Systems и будет подробно рассмотрен ниже.

«М самосвалов для N экскаваторов». Происходит одновременное распределение М самосвалов, которые требуют назначения, между N экскаваторами. Это может быть осуществлено с помощью комбинаторных методов оптимизации. Данная стратегия позволяет принимать решения исходя из глобального взгляда на ситуацию, так как соответствующие алгоритмы учитывают взаимодействия между различными аспектами задачи.

Задача диспетчеризации при этом формулируется либо как задача о назначениях, либо как транспортная задача. В первой формулировке самосвалы распределяются между экскаваторами по принципу «один к одному», то есть каждый экскаватор может получить лишь один самосвал, а каждый самосвал может быть направлен лишь к одному из экскаваторов. Следовательно, М ≥ N. Во второй формулировке решается задача доставки некоторого количества продукции от группы поставщиков к группе потребителей. Цель – минимизировать общие затраты на доставку, реализуя все возможности поставщиков и одновременно удовлетворяя все потребности потребителей. В данном случае поставщиками будут М самосвалов, а потребителями – N экскаваторов. Единицей продукции будет один самосвал.

Каждый поставщик предлагает одну единицу продукта, а каждому потребителю нужно некоторое количество таких единиц, так что общее число единиц, требующихся потребителям, равно М.

Ввиду комбинаторной природы задачи величины М и N не должны быть слишком большими, иначе задача не решится в приемлемые сроки. Каждое из назначений самосвалов, возможных в рамках стратегий «1 самосвал для N экскаваторов» и «М самосвалов для 1 экскаватора», находится среди огромного числа других возможностей, предоставляемых стратегией «М самосвалов для N экскаваторов». Это означает, что данная стратегия должна обеспечить (по крайней мере, теоретически) более эффективное распределение карьерных самосвалов между экскаваторами, нежели две предыдущие.

2. Способы организации погрузочно-транспортных процессов на карьерах

Фиксированное распределение (закрытый цикл). При этом способе организации в начале каждой смены за каждым маршрутом транспортирования (и экскаватором в его начале) закрепляется некоторая группа самосвалов – на определенных основаниях, таких как производственная необходимость, наличие самосвалов и т. д. Эти самосвалы будут работать с одним и тем же экскаватором и маршрутом в течение всей смены, если не выйдет из строя экскаватор или не произойдет другое критическое событие.

Количество самосвалов, приписанных к конкретному экскаватору, зависит от переменных производительности рассматриваемого экскаватора, желаемого уровня его выработки, ожидаемого времени пробегов и времени ожидания для самосвалов в транспортной сети. Из-за стохастического характера транспортных операций и случайного возникновения простоев с некоторой периодичностью происходит образование очередей у конкретного экскаватора.

Несмотря на некоторые попытки усовершенствовать этот метод оперативного планирования работы ЭАК, он признан всеми исследователями наименее эффективным и обычно используется в качестве «нулевой отметки» для изучения эффективности других алгоритмов и подходов.

Гибкое распределение (открытый цикл). При этом способе организации часть имеющихся самосвалов в начале смены ставится на конкретный маршрут (и экскаватор в его начале), но вместо того чтобы обслуживать один экскаватор или один маршрут в течение всей смены, эти самосвалы запрашивают новое назначение каждый раз, когда заканчивают загружаться в пункте погрузки или разгружаться в пункте разгрузки. Такой способ работы, как показывают исследования, значительно повышает производительность карьерных ЭАК. В работе [6], к примеру, заявлено о повышении производительности на 13% на медном карьере Bougainville, на 10–15% – на золотом руднике Barrick Goldstrike, на 10% – на железорудном карьере LTV Steel Mining и на 10% – на разрезе Quintette. Авторы работы [7] в имитационном исследовании работы медного карьера Sungun показали, что за счет открытого цикла продуктивность карьера увеличилась на 8%. В работе [8] были изучены различные эвристические принципы диспетчеризации: минимальное время ожидания экскаватора (MSWT), минимальное насыщение экскаватора (MSS), минимальная требуемая выработка экскаватора (MSPR), минимальное время ожидания самосвала (MTWT), минимальное время цикла самосвала (MTCT), а также алгоритм системы DISPATCH; исследование показало, что независимо от того, какой тип гибкого распределения самосвалов используется, он всегда повышает производительность по сравнению с фиксированным распределением (FA) (табл. 1).

Таблица 1 Влияние гибкого распределения на производительность карьера [8]

Table 1 Effect of flexible allocation on open pit mine production [8]

С конца 1960-х годов как в промышленности, так и в теории было проведено множество исследований для повышения производительности и снижения затрат на добычу полезных ископаемых за счет разработки моделей и алгоритмов гибкого распределения карьерных самосвалов, основанных на различных стратегиях.

3. Модели, используемые в действующих системах

В мире есть несколько компаний, производящих системы управления работой карьеров. Лидером является система DISPATCH компании Modular Mining Systems, повышающая производительность на 12% и используемая на 200 карьерах по всему миру. На втором месте – Jigsaw Jmineops от Hexagon Mining со 130 карьерами. Wenco, представив FleetControl, заявила о повышении производительности на 11%. В настоящее время их система используется на 65 карьерах. Tata Consultancy Services представила Dynamine с диапазоном повышения производительности 10–15%. Micromine с системой Pitram и Caterpillar с системой MineStar Edge – будущие лидеры в области систем управления работой карьеров [9]. Обязательно стоит упомянуть и отечественную систему КАРЬЕР от компании ВИСТ Групп/Цифра.

Эти коммерческие компании обычно не желают раскрывать логику своего программного обеспечения для управления оборудованием. Однако в начале 1990-х годов Modular Mining Systems раскрыла модели и алгоритмы, на основе которых работает система управления карьером DISPATCH. Это классическая система с планом, работающая в реальном производстве, и на ней хотелось бы остановиться подробнее [6].

Рис. 3 Структурная схема системы DISPATCH [6] Схема процесса оперативного планирования работы карьера

Fig. 3 A block schematic diagram of the DISPATCH system [6]

На рис. 3 и 4 представлены общая структурная схема системы DISPATCH и схема алгоритма оптимизации работы карьера в ее составе.

Рис. 4 Процедура распределения самосвалов в системе DISPATCH [6]

Fig. 4 ump truck allocation procedure in the DISPATCH system [6]

Поиск кратчайших путей. В теории графов задача поиска кратчайшего пути – это задача поиска пути между двумя вершинами (узлами) графа, при котором сумма весов составляющих его ребер минимальна. Система DISPATCH использует алгоритм Дейкстры для минимизации времени прохождения пути между каждой парой начальных и конечных пунктов. После решения этой задачи в модель следующего шага поступают следующие данные: 1 – минимальные расстояния и времена пробегов для каждого конкретного транспорта; 2 – узлы, которые самосвалы должны будут проходить, чтобы добираться до мест назначения.

Оптимизация грузопотоков и расстановки самосвалов. На верхнем уровне системы DISPATCH для формирования производственного плана на определенный период используется линейное программирование (ЛП), создавая две отдельные, но тесно взаимосвязанные модели. Первая оптимизирует общую выработку предприятия; вторая – максимизирует производительность технологического оборудования за счет минимизации суммарных объемов, требуемых к выработке. Вторая модель генерирует теоретический план добычи и перевозок, который учитывает производственные ограничения и позднее используется как база для распределения самосвалов в реальном времени.

Первая модель верхнего уровня формулируется как псевдо-стоимостная задача ЛП; целевая функция определяется суммой затрат на все 4 производственные операции в карьере. Решение первой модели представляет собой требуемые показатели выработки экскаваторов, учитывающие максимальные скорости экскавации, максимальную мощность обогатительной фабрики (ОФ), а также нижние и верхние границы качества руды. Во второй модели ЛП минимизируются суммарные транспортные ресурсы, требуемые для того, чтобы обеспечить требуемую выработку экскаваторов. Это значит, что во второй модели с помощью ЛП максимизируется выработка предприятия за счет назначения минимального количества самосвалов на каждый активный маршрут, чтобы выполнить план выработки по маршрутам.

Одно из преимуществ модели в том, что она отражает текущее состояние карьера, используя данные реального времени. Кроме того, оптимальная выработка на каждом маршруте задается количеством горной массы, а не количеством самосвалов. Это поможет на нижнем уровне направить подходящий самосвал для сокращения отставания от плана. Основной недостаток модели – неучет ограничения коэффициента вскрыши. Установив нижнюю границу скоростей экскавации в нуле, разработчики позволили модели игнорировать экскаваторы, работающие на вскрыше. Кроме того, требование ОФ к качеству руды ограничено предопределенными верхними и нижними границами. Это неизбежно вызовет краткосрочное воздействие и на выход ОФ (количество конечного продукта), и на вход (использование некоторых конкретных экскаваторов, которое должно выполняться каждую минуту).

Диспетчеризация в реальном времени. После решения задачи верхнего уровня, выходом которого являются оптимальные грузопотоки по маршрутам, задействуется динамическое программирование (ДП) для адресации самосвалов в подходящие пункты назначения. При этом определяются 2 списка и 3 параметра. Формируются списки: 1) «нуждающихся» экскаваторов (маршрутов), выбранных моделью ЛП; 2) самосвалов, разгружающихся в пунктах разгрузки либо совершающих груженый пробег до пункта разгрузки. Также вычисляется «время требования», то есть ожидаемое время до возникновения следующего требования самосвала на каждом маршруте. Самый нуждающийся маршрут, идущий первым в списке самых нуждающихся экскаваторов, будет маршрутом с наименьшим временем требования. Затем определяются «потерянные тонны», которые используются как критерий выбора «лучшего» самосвала для самого нуждающегося маршрута.

Лучшим является самосвал, наилучшим образом ликвидирующий потерянные тонны самого нуждающегося экскаватора. После того как лучший самосвал назначен к самому нуждающемуся экскаватору, этот экскаватор перемещается на последнее место в списке маршрутов, и процесс повторяется для второго, который теперь становится самым нуждающимся, и т. д. – до тех пор, пока все самосвалы в списке не получат назначение.

Скользящий горизонт планирования, когда требуются последовательные назначения самосвалов, является преимуществом модели нижнего уровня системы DISPATCH. Однако модель не учитывает влияние текущего назначения на последующие, хотя учитываются все самосвалы, направленные к экскаваторам до него. Другой недостаток модели в том, что, несмотря на утверждения разработчиков, метод ее решения – не ДП. Это эвристический принцип, решающий каждую последующую задачу на основе лучших решений предыдущих. В работе [2] отмечается, что неправильное отнесение метода решения к ДП произошло из-за недопонимания принципа оптимальности Беллмана. Тем не менее система DISPATCH зарекомендовала себя неплохо и внедрена более чем на 200 карьерах по всему миру [9].

4. Теоретические модели

Учеными опубликовано множество алгоритмов и моделей для решения задач поиска кратчайших путей, оптимизации грузопотоков и расстановки самосвалов, а также диспетчеризации в реальном времени. На практике они почти не применяются, поэтому слишком подробно на них останавливаться не будем, обозначив лишь некоторые общие черты. Подробное описание этих методов можно найти в работах [4; 5; 7].

4.1. Теория – поиск кратчайших путей

Одно из первых появлений данной проблемы в литературе по ОГР было в работе [10], где кратчайший путь определялся как маршрут от пункта погрузки до пункта разгрузки с наименьшим временем движения. В своей нелинейной стоимостной модели авторы работы [11] решали сетевую задачу нелинейного программирования (НЛП), чтобы найти кратчайшие пути между всеми погрузочными и разгрузочными пунктами. Однако большинство алгоритмов, разработанных теоретиками к данному моменту, используют алгоритм Дейкстры для нахождения кратчайшего пути между «источником» и «стоком» и выбора наилучшего маршрута, соединяющего экскаваторы и пункты разгрузки.

4.2. Теория – оптимизация грузопотоков и расстановки самосвалов

Модель, предложенная в работе [11], решает задачу верхнего уровня в два шага. На первом шаге она фиксирует расположение экскаваторов с помощью комбинаторной модели целочисленного линейного программирования (ЦЛП) с учетом наличия самосвалов; цель – максимизировать выработку с учетом ограничений по качеству. На втором шаге составляется график движения самосвалов между экскаваторами и пунктами разгрузки путем решения задачи НЛП. Целевая функция модели состоит из 3 компонентов: 1) расчетная целевая выработка экскаваторов; 2) расчетные авточасы имеющихся самосвалов, включая и время простоев; 3) штраф за отклонение качества добытой руды от целевых показателей. В работе [4] отмечается, что НЛП предпочтительнее ЛП, так как решения для маршрутов не будут экстремальными; грузопотоки будут распределены по маршрутам равномернее, что позволит проще добиться требуемого качества продукта. Кроме преимуществ модели, отмечено, что все самосвалы в ЭАК имеют одинаковую грузоподъемность (однородный парк самосвалов). Второй недостаток – качество руды неизменно в каждом забое. Однако стохастичность качества руды даже в отдельно взятом блоке не может и не должна игнорироваться.

Теория массового обслуживания (ТМО). В работе [12] карьер представлен как система нескольких сетей. Пропускную способность транспортной системы и время цикла каждой транспортной единицы рассчитывают с помощью метода анализа средних значений, основанного на рекурсивных связях между временами ожидания. Главный недостаток модели – недооценка выработки по причине недопустимости рассмотрения времени движения как системы массового обслуживания (СМО) с бесконечным числом каналов. Модель, предложенная в работе [13] имеет тот же недостаток, что и модель [12], а кроме того, использует распределение Эрланга, которое может легко быть нарушено в реальных условиях.

В работе [14] предложили модель СМО, представив ЭАК как производственную сеть, где самосвалы – это клиенты, а экскаваторы, дробилки, отвалы, трассы и зоны ТО – каналы обслуживания. Принято, что система открытых горных работ (ОГР) – стохастическая марковская система. Однако по таким причинам, как различные распределения времени обслуживания в различных зонах обслуживания, стохастический процесс, характеризующий ОГР, не является марковским.

Авторы работы [15] применили ТМО для анализа степени использования ЭАК в среде, созданной стохастическим поведением погрузочных машин и самосвалов. Применение модели на практике (в Австралии) показало, что игнорирование очередей самосвалов у бункеров – или мощности ОФ – приводит к завышенной оценке выработки.

Модель в работе [16] также имеет ряд недостатков: допущение, что все стохастические производственные процессы являются марковскими, что на самом деле не так; все самосвалы – одного типоразмера; время циклов самосвалов рассчитывается для фиксированных закрытых маршрутов и замкнутой в себе расстановки, при которых не берется в расчет время, требуемое для движения из далеко расположенного предыдущего пункта назначения.

Подводя итог: хотя ТМО и является мощным методом, но – благодаря достижениям в области моделирования – исследователи предпочитают использовать именно моделирование в качестве инструмента учета стохастической природы процессов, а не ТМО.

Транспортный подход. Хотя этот подход решает задачу оптимизации выработки на основе ЛП, его, по причине отличающейся постановки задачи, стоит рассмотреть отдельно. Автор работы [17] предложил модель, цель которой – минимизация общей транспортной работы на маршруте транспортирования. Транспортная работа определяется как «расстояние, на которое горная масса перевозится, умноженное на количество горной массы». Метод использует модель ЛП для постановки оптимального количества самосвалов на маршрут – для покрытия плановой выработки. Модель учитывает производительность каждого экскаватора, а также требования по качеству. Один из главных недостатков модели – общий производственный план, включая верхние и нижние уровни, в модели рассчитывается для однородного парка самосвалов. Модель не гарантирует оптимальность в реальных условиях, где парк разнотипный, так как она распределяет самосвалы по каждому экскаватору так, как если бы они все были одинаковой грузоподъемности. Другой большой недостаток – модель не рассматривает поломки самосвалов как значительные события, меняющие ситуацию в карьере.

Линейное программирование. ЛП (а особенно ЦЛП) применяется для оптимизации управления карьерами чаще всех остальных подходов. Наиболее известная модель ЛП была предложена автором работы [18], который применил модель ЛП для максимизации производительности экскаваторов. Модель учитывает требуемые пределы качества руды для ОФ. Также она учитывает коэффициент вскрыши и относительные приоритеты экскаваторов, особенно работающих по руде. Было сделано допущение, что производительность экскаваторов будет возрастать линейно по мере увеличения количества самосвалов. Однако при разнотипном парке добавление самосвалов разных типоразмеров в имеющийся парк будет увеличивать выработку нелинейно. Другой большой недостаток модели – в целевой функции также надо было учесть факторы накопления и перевалки руды.

Один из главных недостатков всех моделей ЛП, – чтобы учесть производственные ограничения, такие как коэффициент вскрыши и требуемое качество руды, модели должны определить приемлемые границы. Однако определение границ делает производство далеким от оптимального, особенно если требование ОФ к качеству изменяется. Для разъяснения, допустим, что цель – максимизировать выработку. Тогда вероятность назначения самосвала к экскаватору, стоящему ближе к дробилке (что даст меньшее время цикла для самосвала), будет выше. Если среднее качество в этих ближних забоях достаточно близко к одной из допустимых границ, то, каким бы ни был диспетчерский алгоритм, пребывание качества в допустимых пределах трудно контролировать. Как следствие, затраты на накопление (а следовательно, и на перевалку), связанные с этим, становится невозможно игнорировать.

Целевое программирование (ЦП). В простейшей задаче ЦП планировщик определяет некоторые цели, которых он хочет достичь, для каждой целевой функции. Оптимальное решение минимизирует отклонения от установленных целей; то есть это решение не максимизирует или минимизирует какой-либо показатель, а пытается найти некое целевое его значение. В задачах оптимизации ОГР существует множество целей, которых нужно достичь: максимизация выработки и поддержание качества руды в желаемых пределах, оптимизация использования ОФ и минимизация затрат на перемещение самосвалов и экскаваторов.

В работе [19] сформулирована модель оптимизации производства карьера, основанная на ЦП. Модель максимизирует производительность экскаваторов с учетом качества руды, скорости экскавации, пропускной способности пунктов разгрузки и требований к коэффициенту вскрыши. Преимущества модели – она учитывает разнотипность парка самосвалов и оптимизирует две основные цели работы карьера одновременно, не пренебрегая ни одной из них. Помимо устранения недостатков предыдущих моделей, данная модель избегает еще одного недостатка моделей ЛП – определения верхней и нижней границ целевого качества шихты, отправляемой на ОФ. Однако модель не учитывает всех целей, которые должны быть учтены в работе карьера, таких как затраты на перемещение оборудования и т. д.

Стохастическое программирование. Авторы работы [20] применили стохастическую оптимизацию с вероятностными ограничениями для расстановки самосвалов по карьеру. Также они использовали средство обновления модели и параметров в момент изменения смены или статуса карьера. Представленная модель рассматривает загрузку самосвала и время его цикла как вероятностные показатели. Переменные решения в модели – количества и типы самосвалов, расставляемых по экскаваторам. Авторы сообщают, что их стохастическая модель может быть решена путем перевода ее в квадратичный детерминированный вид и использования методов целочисленного НЛП. Однако решение модели НЛП требует больших затрат времени. Поэтому изначальная модель была разделена на две подмодели, которые решаются для расстановки дискретного количества самосвалов к каждому пункту погрузки.

Хотя модель и предоставляет хорошую концептуальную базу стохастического оптимизационного подхода к решению мультиуровневых задач оптимизации, она принимает в расчет только вероятностную природу времени пробега самосвалов. Кроме того, модель сформулирована под конкретное предприятие и не может быть распространена на другие.

4.3. Теория – диспетчеризация в реальном времени

Есть два основных подхода к осуществлению диспетчерских процедур: задача о назначениях и транспортная задача. Первый подход сам по себе является частным случаем транспортной задачи в исследовании операций.

Задача о назначениях. В общем случае – это сбалансированная транспортная задача, в которой все «потребности» и «источники» имеют мощность, равную 1. В каждой задаче о назначениях есть ценовая матрица, состоящая из удельных затрат, связанных с назначением каждой поставки на каждую потребность. Цель любой задачи о назначениях – минимизировать затраты на распределение поставок по потребностям. С точки зрения горного дела, задача о назначениях используется в основном для распределения самосвалов (поставок) по экскаваторам или разгрузочным пунктам (потребностям). Цель диспетчеризации карьерных самосвалов, основанной на задаче о назначениях, состоит в минимизации простоев экскаваторов, простоев самосвалов, заторов и т. д. Почти все модели диспетчеризации реального времени – и в промышленности, и в теории – основаны на задаче о назначениях.

Автор работы [10] предложил последовательность задач о назначениях для диспетчеризации самосвалов, требующих назначения. Целевая функция модели – минимум суммарных простоев экскаваторов для минимизации «потерянных тонн» производства. Два главных недостатка модели: 1) назначения не максимально точны, так как принятые решения не пересматриваются, хотя количество действующих самосвалов меняется и решения теряют актуальность; 2) модель не способна использовать ДП для решения задачи о назначениях, так как не имеет возможности использовать все возможные решения на предыдущих стадиях.

В работе [11] представлена модель назначений, которая учитывает 10–15 «будущих» самосвалов и их влияние на текущее назначение. Цель – минимизировать сумму квадратичных отклонений ожидаемого времени простоя самосвалов от планового времени простоя. Главное преимущество модели в том, что она учитывает влияние «будущих» самосвалов на текущее назначение. Однако допущение, что парк однородный, является недостатком модели. Второй крупный недостаток, имеющий место почти во всех моделях, основанных на задаче о назначениях, – хотя модели учитывают «будущие» самосвалы при принятии текущего решения о назначении, они не учитывают влияние текущего решения на последующие.

Автор работы [17] предложил принцип диспетчеризации, основанный на разнице между реальным и оптимальным интервалами прохождения самосвалов по маршрутам. Алгоритм направляет самосвалы к тому погрузчику/дробилке, где это отклонение максимально. Автор заверяет, что предложенный алгоритм поддерживает потоки самосвалов как можно ближе к оптимальному уровню. Однако важным недостатком модели является то, что она недооценивает «потерянные тонны», возникшие по причине простоев самосвалов, так как игнорируются очереди в пунктах назначения, особенно в погрузочных.

Авторы работы [21] представили полуавтоматическую модель, где – к тому моменту, как самосвалу потребуется назначение – в имитационной модели карьера решаются 3 эвристических критерия диспетчеризации. Результаты моделирования выводятся на панель в виде таблицы вместе с результатом моделирования по закрытому циклу, оставляя решение за диспетчером. Все эвристические критерии в известных работах основаны на максимизации использования самосвалов или экскаваторов за счет решения задачи о назначениях. Хотя они и повышают производительность в сравнении с закрытым циклом, они имеют ряд недостатков, таких как игнорирование качества руды. Другой крупный недостаток этого типа целевых функций – они склонны направлять самосвалы по кратчайшим маршрутам, и, как следствие, экскаваторы, работающие в дальних забоях, будут простаивать дольше [21].

Хотя применение задачи о назначениях дает быстрое решение для назначения самосвалов, такая стратегия имеет 2 крупных недостатка, вытекающих из самой природы задачи о назначениях. Во-первых, в каждый момент времени к каждому экскаватору направляется всего 1 самосвал, даже если экскаватор далеко отстает от своего производственного плана и ему нужно больше самосвалов. Во-вторых, несмотря на заверения некоторых авторов, модели не в состоянии учесть влияние самосвалов, которые будут распределены в будущем.

Транспортная задача. В этой области заслуживает доверия модель, представленная в работе [22]. В этой модели, во-первых, определяется «нуждающийся» экскаватор (находящийся на маршруте, имеющем на данный момент накопленную выработку ниже плановой). После этого, на следующем шаге, определяется количество самосвалов, которое требуется каждому «нуждающемуся» экскаватору. Наконец, определяется потребность для каждого экскаватора, а также общая потребность производства на текущий момент.

Модель гарантирует, что общее количество назначенных самосвалов не превышает количества имеющихся самосвалов, а самосвалы, направленные к экскаватору, компенсируют его «потерянные тонны» как можно полнее. Модель оперирует разнотипными парками; как результат, она будет так же близка к реальности, как и модель верхнего уровня тех же авторов [19]. Также допускается ситуация, когда экскаватор сильно отстает от плана и требует назначения более чем одного самосвала. В такой ситуации модель легко адресует более одного самосвала к «нуждающимся» экскаваторам, сильнее всех отстающим от плана, без каких-либо ограничений, возникающих при использовании задачи о назначениях.

Тем не менее у модели есть 2 крупных недостатка. Первый недостаток в том, что базой для расчета отклонений по маршрутам является усредненное значение выработки по всем маршрутам. Однако по производственному плану иногда требуется извлекать гораздо больше какого-либо материала для максимизации выработки на конкретном маршруте. Второй недостаток – затраты на транспортирование любого количества горной массы вычисляются как постоянные и независимые от «центров поставок». Однако время ожидания любого самосвала у экскаватора или дробилки зависит от самосвалов, назначенных до того, особенно в перегруженных самосвалами системах. Кроме того, время ожидания зависит от самосвалов, уже находящихся в пунктах назначения (или на пути к ним), так что нет возможности учесть время ожидания, вызванное самосвалами, назначенными позже и способными раньше достичь пункта назначения.

5. Средство оценки систем диспетчеризации – имитационное моделирование

Из вышеизложенного можно сделать следующий вывод: существующие системы, модели и алгоритмы диспетчеризации, учитывая все предыдущие решения по назначению самосвалов к экскаваторам, даже приблизительно не способны учесть, к чему эти решения приведут в будущем. Кроме того, недостаточно учитывается вероятностная природа производственных процессов в карьерах. Чтобы устранить эти недостатки, необходимо более активно использовать имитационное моделирование (ИМ).

Применение ИМ в горнодобывающей промышленности берет начало еще в 1940-х годах, но первое применение дискретно-событийного ИМ, ныне традиционно используемого для оценки систем диспетчеризации (СД), произошло лишь в начале 60-х, когда для решения транспортных проблем на горнодобывающих предприятиях был применен метод Монте-Карло.

После этого было выполнено множество работ, посвященных использованию ИМ в горном деле. В 2007 г. для симуляции расширения карьера была разработана имитационная модель, названная «симулятором открытых горных работ» [23]. Исследование показало, что в случае динамичности моделируемых процессов и случайности входных параметров симуляторы на основе искусственного интеллекта могут быть весьма эффективны и полезны.

6. Ограничения существующих моделей

Связь между планами стратегического и оперативного уровня. Одно из главных «узких мест» в планировании работы карьера – как связать стратегический план с оперативным, чтобы как можно оптимальнее распределять самосвалы. Стратегическая часть представляет собой набор блоков, которые должны быть выработаны при определенном горизонте планирования, чтобы получить наивысший доход. С другой стороны, оперативная часть пытается расставлять и назначать самосвалы на крупные полигоны, каждый из которых содержит несколько блоков, для достижения стратегических целей. Связь двух вышеупомянутых уровней планирования требует согласования краткосрочного плана стратегической части с распределением самосвалов оперативной части. Таким образом, СД, управляющая в оперативной части, должна обеспечивать такое управление производством, чтобы достичь и краткосрочных, и долгосрочных целей. Существующие модели оптимизации производства не дают гарантий достижения главной цели. Краткосрочный производственный план, являющийся наиболее близкой частью стратегического планирования к оперативному, обеспечивает доставку горной массы из забоев, но в реальности он досконально не соблюдается.

Учет неопределенностей. Большинство существующих моделей оптимизации производства – детерминированные, и не покрывают всю деятельность карьера. Но горные работы имеют стохастическую природу, и состоят из множества периодов. Каждый период влияет на последующие, вплоть до закрытия карьера. Качество горной массы в каждом забое также стохастично, как и производственные процессы. Большинство моделей берет в расчет постоянное усредненное качество в каждом забое, что приводит к неоптимальности в расчетах.

Мобильность и наличие оборудования. Одним из основных факторов, вызывающих отклонения от производственного плана, являются «потерянные тонны», связанные с перемещением экскаваторов из одного забоя в другой, либо с одного уступа на другой. Эти перемещения делают погрузочную машину недоступной. Кроме того, экскаваторы очень медленны, как и любое дорогостоящее оборудование. Поэтому передислокация экскаваторов приводит к значительным «потерянным тоннам», что отбрасывает маршрут с экскаватором в конце далеко назад от целевой выработки, а также увеличивает эксплуатационные расходы. Учет затрат и «потерянных тонн», связанных с перемещением экскаваторов, в модели планирования производства поможет управленцам сделать выбор, близкий к оптимальному.

Моделирование, близкое к реальности. Хотя на большинстве карьеров используются разнотипные самосвалы, почти все модели, разработанные для решения задач производственного планирования, избегают рассмотрения смешанных парков горного оборудования.

Все модели, разработанные для оптимизации СД карьеров, проходили валидацию с помощью имитационной модели существующего карьера. Почти во всех имитационных моделях, использованных для валидации оптимизационных моделей, игнорируется моделирование ОФ и бункеров. Чтобы грамотно оценить разработанную модель, имитационная модель всего производства карьера должна быть как можно ближе к реальности.

Динамическое определение кратчайших путей. На малых карьерах с ограниченным числом дорог и небольшим ЭАК кратчайший путь между каждой парой пунктов погрузки и назначения может быть принят неизменным. Однако на крупных карьерах присутствует густая сеть технологических трасс и большой парк самосвалов, передвигающихся в рабочей зоне. Большой автопарк обычно содержит многообразие типоразмеров самосвалов с различными средними и максимальными скоростями, что может вызвать заторы на некоторых участках трасс. Эти несоразмерности вызовут потери производительности.

Чтобы решить эту проблему, кратчайшие пути можно определять динамически. Другими словами, слежение за самосвалами, работающими в системе, поможет определить кратчайший путь между текущим местоположением самосвала и его следующим пунктом назначения – основываясь на времени пути до пункта назначения, с учетом имеющихся заторов на участках трасс.

Оперативная диспетчеризация на основе задачи о перевозках. В процессе диспетчеризации рекомендуется использовать задачу о перевозках с промежуточными пунктами – вместо транспортной задачи или задачи о назначениях. В задаче о перевозках, кроме пунктов поставки и потребления, существуют промежуточные пункты, через которые грузы транспортируются от поставщиков к потребителям. В горном деле в качестве таких пунктов можно принять скопления руд или пересечения трасс.

Заключение

В данной статье классифицируются и обсуждаются различные используемые в промышленности и разработанные теоретически модели и алгоритмы для СД карьеров. И теоретические, и коммерческие алгоритмы используют одну из следующих стратегий для решения динамической задачи производственного планирования на карьерах.

1. Мультиуровневый подход. Во-первых, определяются кратчайшие пути между каждой парой «источников» и «стоков». Во-вторых, определяется оптимальный грузопоток на каждом пути. Затем часть имеющегося автопарка ставится на маршрут (статическая часть). Наконец, самосвалы распределяются по маршрутам так, чтобы выполнить установленный план выработки (динамическая часть). Большинство СД следуют этой стратегии.

2. Одноуровневый подход. Находится кратчайший путь между экскаваторами и пунктами назначения, после чего статическая и динамическая части решаются одновременно.

Несмотря на количество работ, выполненных в области улучшения качества СД карьеров, необходимы более эффективные и практичные модели для решения проблем и в статической, и в динамической частях. Заторы, происходящие по вине медленных самосвалов на линиях, на крупных карьерах являются проблемой, привносящей динамичность в задачу нахождения кратчайших путей. Кроме того, слабая увязка между планами оперативного и стратегического уровней является важным фактором, который должен быть учтен в моделях принятия решений. Чем меньше отклонение алгоритма управления СД от стратегических целей, тем ближе реальный доход, полученный от производства, будет к стратегически запланированному. Далее, и технические, и геологические неопределенности являются неотъемлемыми компонентами, которые должны быть точно учтены в СД. Еще один важный фактор – «потерянные тонны», вызванные перемещением экскаваторов, а также затраты, связанные с их перемещением в новый забой. Хотя добавление вышеупомянутых компонентов увеличивает время расчетов в любой модели, основанные на ИМ методы оптимизации, методы ЦП и основанные на задаче о перевозках алгоритмы оперативной диспетчеризации можно назвать мощными инструментами для эффективного управления карьерными ЭАК.